Рассмотрим ситуацию, когда нам известны длины двух сторон треугольника, и нам необходимо найти величину угла, образованного этими сторонами. Это задача, с которой часто сталкиваются в школьных и университетских курсах геометрии. На первый взгляд может показаться, что решить эту задачу просто: достаточно применить изученные формулы или теоремы. Однако на практике это может быть не так тривиально, особенно если имеется некоторая неточность или нехватка информации. Будем разбираться, как найти угол треугольника по сторонам двум.
Существует несколько способов решения этой задачи, однако самым удобным и простым способом является применение закона косинусов. Закон косинусов гласит, что квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон, умноженных на два произведения этих сторон и косинуса величины искомого угла.
Поэтому, чтобы найти угол треугольника по сторонам двум, необходимо составить уравнение по закону косинусов, подставить известные значения и решить его относительно искомого угла. В результате получим величину искомого угла, которую можно использовать для решения дальнейших задач или вычислений.
Как вычислить угол треугольника по длинам сторон
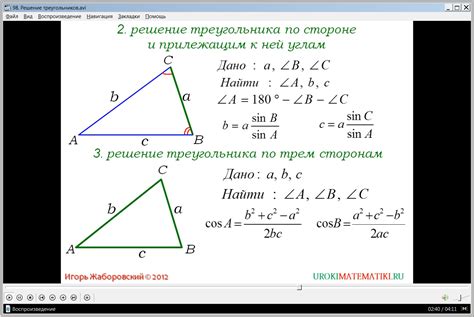
Вспомним теорему косинусов:
Теорема косинусов: В треугольнике с длинами сторон a, b и c и углом α, который соответствует стороне c, выполнено следующее равенство:
c2 = a2 + b2 - 2ab·cos(α)
Для вычисления угла треугольника по длинам сторон, необходимо решить уравнение теоремы косинусов относительно угла α. Обычно в таком случае используют обратную функцию косинуса (арккосинус), которую можно обозначить как acos.
Шаги для вычисления угла треугольника по длинам сторон:
- Узнайте длины сторон треугольника.
- Выберите сторону треугольника, к которой вы хотите вычислить угол.
- Примените теорему косинусов и решите уравнение относительно угла α:
- Вычислите значение угла α, используя найденные значения длин сторон.
α = acos((a2 + b2 - c2) / (2ab))
Теперь вы знаете, как вычислить угол треугольника по длинам сторон, используя теорему косинусов. Этот метод может быть полезным при решении различных задач, связанных с треугольниками.
Методы определения углов треугольника

Ниже описаны несколько методов определения углов треугольника:
- Теорема синусов:
- Для определения угла треугольника можно использовать теорему синусов.
- Этот метод основывается на соотношении между сторонами и синусами углов треугольника.
- По известным сторонам треугольника можно найти синусы углов, а затем найти значения углов.
- Теорема косинусов:
- Для определения угла треугольника также можно применять теорему косинусов.
- Этот метод основывается на соотношении между сторонами и косинусами углов треугольника.
- По известным сторонам треугольника можно найти косинусы углов, а затем найти значения углов.
- Теорема углов треугольника:
- Третий метод определения углов треугольника основывается на теореме углов треугольника.
- Согласно этой теореме, сумма углов треугольника равна 180 градусам.
- Поставив уравнение на сумму углов треугольника, можно найти один из углов, основываясь на значениях других углов и известных данных.
Использование одного из этих методов позволяет определить углы треугольника, даже если изначально даны только стороны треугольника.
Основные формулы для вычисления углов треугольника
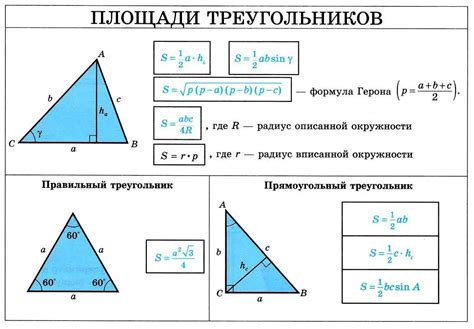
В геометрии существует несколько формул, которые позволяют вычислить углы треугольника по заданным сторонам.
1. Формула косинусов: данная формула позволяет найти угол треугольника, если известны длины всех трех его сторон. Формула выглядит следующим образом:
| a2 = b2 + c2 - 2bc cos(A) |
| b2 = a2 + c2 - 2ac cos(B) |
| c2 = a2 + b2 - 2ab cos(C) |
где a, b, c - длины сторон треугольника, A, B, C - соответствующие углы.
2. Формула синусов: данная формула позволяет вычислить угол треугольника, если известны длины двух его сторон и угол между ними. Формула выглядит следующим образом:
| sin(A) = (a * sin(C)) / c |
| sin(B) = (b * sin(C)) / c |
| sin(C) = (c * sin(A)) / a = (c * sin(B)) / b |
где a, b - длины сторон треугольника, C - угол между ними.
3. Формула тангенсов: данная формула позволяет вычислить угол треугольника, если известны длины двух его сторон и угол между ними. Формула выглядит следующим образом:
| tan(A) = (a * tan(C)) / c |
| tan(B) = (b * tan(C)) / c |
где a, b - длины сторон треугольника, C - угол между ними.
Используя данные формулы, можно вычислить углы треугольника, зная длины его сторон. Это может быть полезно, например, при решении задач по геометрии или в других областях, связанных с треугольниками.