Величина угла играет важную роль во многих научных и технических областях. Определение угла в градусах является основной и наиболее распространенной системой измерения углов. Правильное определение угла не только облегчает выполнение математических операций, но и позволяет анализировать и предсказывать результаты различных физических явлений.
Существует несколько методов определения величины угла в градусах. Один из наиболее распространенных методов основан на использовании градусного меридиана. В этом методе, циркуль с нониусной шкалой используется для измерения угла между двумя лучами или отрезками. Сначала центр циркуля помещается в точку пересечения лучей или начала отрезка, а затем с помощью нониуса определяется величина угла.
Второй метод основан на использовании тригонометрической функции тангенса. Для определения угла с помощью этого метода, необходимо знать длины противолежащей и прилежащей сторон треугольника. Затем используя формулу тангенса, можно вычислить величину угла. Этот метод особенно полезен в тех случаях, когда применение циркуля не представляется возможным или практичным.
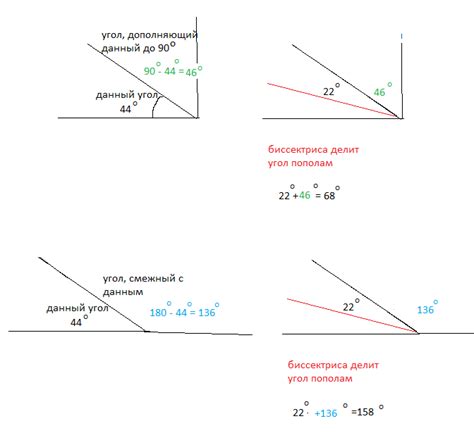
Величина угла в градусах: методы измерения
Существует несколько методов для измерения величины угла в градусах. Один из самых распространенных методов - использование градусного циркуля. Градусный циркуль - это инструмент, состоящий из двух подвижных ножек, позволяющий измерить угол между двумя линиями. Чтобы измерить угол с помощью циркуля, необходимо разместить его вдоль линий и совместить ножки циркуля с концами угла. Затем можно прочитать величину угла непосредственно на шкале циркуля. Градусный циркуль обычно имеет шкалу, разделенную на 360 градусов, где каждая метка представляет собой 1 градус. Этот метод позволяет измерить угол с высокой точностью и простотой.
Другим методом измерения величины угла в градусах является использование угломера. Угломер - это специальное устройство, предназначенное для измерения углов. Он состоит из основания и показателя угла. Основание угломера устанавливается вдоль одной из линий, а показатель угла указывает на величину угла между линиями. Угломеры могут иметь различные шкалы, но наиболее распространенной является шкала градусов. Для того чтобы измерить угол с помощью угломера, необходимо установить его вдоль линий и считать значение на шкале угломера.
Также существуют электронные приборы, позволяющие измерять величину угла в градусах. Эти приборы обычно оборудованы дисплеем, на котором отображается значение угла. Они работают на основе электронных датчиков, которые определяют положение и наклон объектов и вычисляют угол. Такие приборы обладают высокой точностью и удобны в использовании.
Знание величины угла в градусах является важным для многих областей, включая архитектуру, инженерное дело, геодезию и физику. Важно понимать, что измерение угла - это процесс, требующий точности и внимания к деталям. Какой бы метод измерения вы ни использовали, важно следить за правильным расположением инструментов и использовать подходящие методы для обеспечения наибольшей точности измерения.
Метод с использованием геодезического прибора

Для определения величины угла в градусах существует иной метод, который основан на использовании геодезического прибора. Такой прибор позволяет измерять углы с большой точностью и достаточно быстро.
Применение этого метода особенно полезно в ситуациях, когда требуется быстрое и точное измерение угла, например, при строительстве или геодезических работах. Геодезический прибор состоит из оптического прибора с лимбом, который делится на градусы, минуты и секунды и позволяет измерять углы с высокой точностью.
Для определения величины угла с помощью геодезического прибора необходимо установить его на точке, которую вы хотите измерить. Затем, используя визир, прицелиться на предмет, на котором находится вторая точка, и снять показание на лимбе геодезического прибора, соответствующее данному углу.
Определение угла с использованием геодезического прибора является одним из наиболее точных и эффективных методов измерения углов в градусах. Этот метод широко применяется геодезистами и строителями для выполнения различных работ, где требуется определение угла с высокой точностью.
Метод с использованием транспортира

Для определения угла с помощью транспортира необходимо следовать следующим шагам:
- Поместите транспортир на лист бумаги или другую плоскую поверхность так, чтобы его центр совпадал с вершиной угла, который вы хотите измерить.
- Ориентируйте транспортир так, чтобы его нулевая линия (вертикальная или горизонтальная, в зависимости от ориентации угла) совпадала с одной из сторон угла.
- Определите величину угла, считая количество делений между нулевой линией и другой стороной угла.
При использовании транспортира необходимо быть аккуратным и точным. Важно помнить, что погрешность измерения может возникнуть из-за несовершенства самого инструмента и неверного выравнивания с вершиной угла.
Метод с использованием транспортира является одним из наиболее точных и достоверных способов определения величины угла в градусах. Он может быть использован как в школьном образовании для обучения геометрии, так и в научных и инженерных расчетах для определения точных угловых величин.
Метод с использованием геометрических расчетов

Существует метод определения величины угла в градусах с использованием геометрических расчетов. Для этого необходимо знать длины сторон треугольника и его площадь.
Для начала, измерьте длины сторон треугольника с помощью линейки или другого измерительного инструмента. Запишите эти значения, чтобы иметь возможность воспользоваться ими в дальнейших расчетах.
Затем нам понадобится найти площадь треугольника. Существует несколько способов это сделать. Один из самых простых методов - использование формулы площади треугольника через длины его сторон, известную как формула Герона.
Формула Герона имеет вид:
S = √(p(p - a)(p - b)(p - c)),
где S - площадь треугольника,
p - полупериметр треугольника, вычисляемый как p = (a + b + c) / 2,
a, b, c - длины сторон треугольника.
После того, как вы найдете площадь треугольника, можно использовать геометрическую формулу, связывающую площадь треугольника и синус угла:
S = (1/2) * a * b * sin(α),
где α - величина угла в радианах,
a, b - длины двух сторон треугольника, между которыми находится угол α.
Используя синус угла, можно найти его величину в радианах и далее преобразовать ее в градусы, умножив на 180 и разделив на π:
α = arcsin(2S / (a * b)) * (180 / π).
Таким образом, применяя геометрические расчеты, можно эффективно определить величину угла в градусах, имея заранее измеренные значения длин сторон треугольника и его площадь.
Метод с использованием тригонометрии
Для начала, необходимо определить значение искомого угла в радианах. Это можно сделать, используя обратные функции тригонометрии, такие как arcsin, arccos или arctan. Например, для определения угла, имея значение синуса, можно воспользоваться функцией arcsin, которая возвращает угол, значение синуса которого равно заданному.
Далее, найденное значение угла в радианах следует перевести в градусы. Для этого необходимо умножить значение угла в радианах на 180 и разделить результат на число pi (приближенное значение иррациональной константы, равное приблизительно 3,14159).
В итоге, применяя данный метод с использованием тригонометрии, получаем точное значение величины угла в градусах. Этот метод является быстрым и эффективным, особенно если в наличии имеются таблицы значений тригонометрических функций.