Треугольник – это геометрическая фигура, состоящая из трех отрезков-сторон, которые соединяют три точки – вершины. Однако не всегда случается, что три отрезка могут образовать треугольник. Для того чтобы определить, существует ли треугольник по заданным сторонам, необходимо знать некоторые правила и условия.

Первое правило гласит, что две стороны треугольника в сумме всегда должны быть больше третьей стороны. Иначе говоря, сумма любых двух сторон всегда должна быть больше третьей стороны. Если это условие не выполняется, то треугольник с такими сторонами невозможен.

Кроме того, второе правило требует, чтобы разность двух сторон всегда была меньше третьей стороны. Иначе говоря, модуль разности любых двух сторон должен быть меньше третьей стороны. Если это условие не выполняется, то треугольник с такими сторонами также не может существовать.

Итак, для того чтобы определить, существует ли треугольник по заданным сторонам, необходимо провести две проверки: сумму двух любых сторон треугольника и модуль разности двух любых сторон треугольника должны быть соответственно больше и меньше третьей стороны. Если оба условия выполнены, то треугольник с заданными сторонами существует, иначе – нет.

Определение треугольника по сторонам: правила и условия

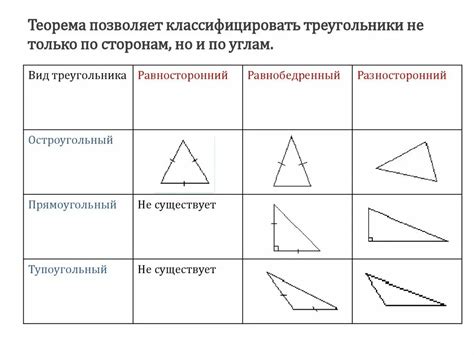
Существует несколько правил и условий, которым должны удовлетворять стороны, чтобы треугольник мог существовать:

1. Неравенство треугольника: Сумма длин двух сторон треугольника всегда должна быть больше длины третьей стороны. Это правило гарантирует, что стороны не пересекутся и будут образовывать фигуру без самопересечений.
2. Тривиальный случай: Стороны треугольника не могут иметь нулевую длину. Если хотя бы одна сторона равна нулю, треугольник не может существовать.
3. Стороны не должны быть отрицательными: Длины сторон треугольника должны быть положительными числами. Если длина хотя бы одной стороны отрицательна, треугольник не может быть сформирован.

Используя эти правила и условия, можно определить, может ли набор отрезков существовать в виде треугольника. Если все условия выполняются, то треугольник существует, иначе набор отрезков не может образовать треугольник.

Как определить возможность существования треугольника

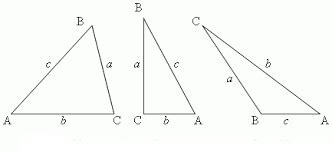
Для определения возможности существования треугольника можно использовать следующие правила:

1. Сумма длин любых двух сторон должна быть больше длины третьей стороны. Другими словами, если a, b и c - длины сторон треугольника, то должно выполняться неравенство a + b > c, a + c > b и b + c > a. Если хотя бы одно из этих неравенств не выполняется, то треугольник с такими сторонами не может существовать.
2. Разность длин любых двух сторон должна быть меньше длины третьей стороны. Согласно этому правилу, если a, b и c - длины сторон треугольника, то должно выполняться неравенство |a - b|

Если все условия для существования треугольника выполняются, то данными сторонами можно построить треугольник. В противном случае треугольник с такими сторонами не существует.

Изучение правил определения возможности существования треугольника позволяет не только проводить геометрические вычисления, но и применять их в практических задачах, например, в строительстве или инженерии.