В математике возрастание и убывание функции - это основные понятия, которые позволяют определить, как меняется значение функции на определенном интервале. При этом, производная функции играет важную роль в анализе возрастания и убывания.
Производная функции в каждой точке определяет скорость изменения данной функции. Если производная положительна на каком-то интервале, то это означает, что значение функции возрастает на этом интервале. Если производная отрицательна, то функция убывает на данном интервале.
Таким образом, знание производной функции позволяет точно определить, когда функция возрастает, а когда убывает. Однако, следует отметить, что наличие производной в точке не гарантирует непрерывное возрастание или убывание функции, так как производная может быть равна нулю в данной точке.
Возрастание и убывание функции
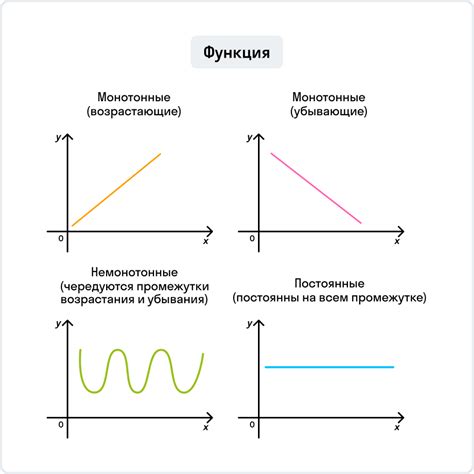
Функция называется возрастающей на интервале, если для любых двух точек этого интервала x₁ и x₂, таких что x₁
Функция называется убывающей на интервале, если для любых двух точек этого интервала x₁ и x₂, таких что x₁ f(x₂). Иными словами, значения функции убывают с увеличением аргумента.
При анализе функций на возрастание и убывание, мы обычно используем производную функции. Если производная положительна на интервале, то функция возрастает на этом интервале. Если производная отрицательна на интервале, то функция убывает на этом интервале. Если производная равна нулю, то функция может иметь экстремумы.
Определение функции
Функция обозначается символом f и записывается в виде f(x), где x – аргумент функции.
Аргументы функции могут быть числами, переменными, выражениями или комбинациями этих элементов. Значения функции также могут быть числами, переменными или выражениями.
Функция может быть задана явно, то есть формулой, которая определяет соответствующее значение функции для каждого аргумента. Например, функция f(x) = x^2 - 2x + 1 задана явно.
Функция может быть задана также таблицей значений, графически или словесно.
Одной из основных задач в анализе функций является изучение их свойств, таких как возрастание и убывание. Для этого используется производная функции, которая позволяет определить изменение значений функции при изменении аргумента.
Производная функции
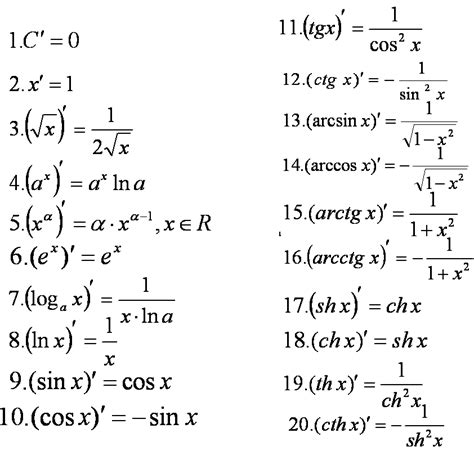
Производная функции определяется как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Формально, если функция $f(x)$ определена в окрестности точки $x_0$, то производная функции в точке $x_0$ обозначается как $f'(x_0)$ и вычисляется следующим образом:
$$f'(x_0) = \lim_{{\Delta x \to 0}}\frac{{f(x_0 + \Delta x) - f(x_0)}}{{\Delta x}}$$
Значение производной функции в точке позволяет определить, возрастает функция в данной точке или убывает. Если производная положительна, то функция возрастает, если производная отрицательна, то функция убывает. Если же производная равна нулю, то функция имеет экстремум - максимум или минимум в данной точке.
Изучение производной функции и ее свойств позволяет более полно понять поведение функции и графика этой функции. Например, знание положительности или отрицательности производной позволяет определить интервалы возрастания и убывания функции, что может быть полезно при решении задач оптимизации или при анализе поведения физических процессов.
Правила определения возрастания функции
Функция возрастает на интервале, если:
- Производная функции положительна на этом интервале. Если производная больше нуля на всем интервале, то значение функции на этом интервале увеличивается. Например, если производная больше нуля на интервале (a, b), то функция возрастает на этом интервале.
- График функции имеет положительный наклон. Если график функции стремится вверх на интервале, то функция возрастает. Например, если график функции поднимается слева направо на интервале (a, b), то функция возрастает на этом интервале.
Примечание: Если в точке x функция имеет положительную производную и график имеет положительный наклон, но в окрестности этой точки производная становится отрицательной или график функции имеет отрицательный наклон, то это указывает на локальный максимум функции.
Правила определения убывания функции
Для определения убывания функции на интервале можно воспользоваться производной функции и ее знаками. Если функция имеет непрерывную производную на интервале, то:
- Если производная функции строго отрицательна на интервале, то функция убывающая на этом интервале.
- Если производная функции равна нулю на интервале и меняет свой знак с минуса на плюс, то функция убывает на левой части интервала и возрастает на правой.
- Если производная функции равна нулю на интервале и меняет свой знак с плюса на минус, то функция возрастает на левой части интервала и убывает на правой.
- Если на интервале производная функции не меняет знак и либо положительна, либо отрицательна, то функция не убывает и не возрастает на этом интервале.
Знание этих правил поможет в определении убывания функции на заданном интервале и сделает решение задач гораздо проще.
Примеры определения возрастания и убывания функции
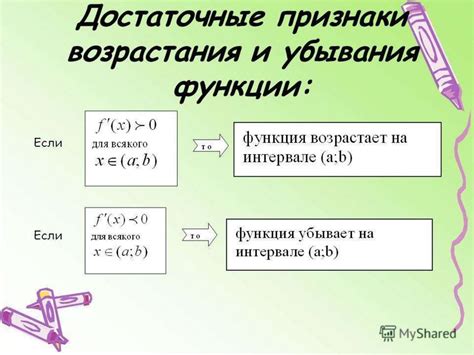
Для определения возрастания и убывания функции по её производной необходимо рассмотреть знаки производной функции. Производная функции показывает, как меняется значение функции при изменении аргумента.
Пусть функция f(x) дифференцируема на интервале I и x является точкой из этого интервала.
Если производная функции f'(x) строго положительна на интервале I (т.е. f'(x) > 0), то функция f(x) возрастает на этом интервале. Это означает, что с увеличением x значение функции f(x) также увеличивается.
Если производная функции f'(x) строго отрицательна на интервале I (т.е. f'(x) ), то функция f(x) убывает на этом интервале. Это означает, что с увеличением x значение функции f(x) уменьшается.
Таким образом, анализ производной функции помогает определить, в каких точках функция возрастает, а в каких убывает. Это важное свойство функции, которое часто используется при решении задач из различных областей математики и науки.