Гармонические колебания являются одним из наиболее распространенных физических процессов, с которыми мы сталкиваемся в повседневной жизни. Это колебания, которые происходят с постоянной частотой и имеют синусоидальную форму. Однако, для полного описания гармонических колебаний необходимо знать не только амплитуду и частоту, но и время, в котором происходит процесс.
Определение времени в уравнении гармонических колебаний возможно через различные способы и принципы. Один из них – использование уравнения колебаний в форме sin(ωt + φ), где ω – угловая частота, t – время, а φ – начальная фаза колебаний. Это уравнение позволяет определить положение колеблющейся частицы в любой момент времени, а следовательно, и время, в которое это происходит.
Другой способ определения времени – использование периода колебаний. Период – это время, за которое колеблющаяся частица совершает одно полное колебание. Он обозначается символом T и является обратной величиной к частоте (T = 1/ω). Путем измерения периода колебаний можно определить время, которое занимает процесс от начала до конца.
Уравнение гармонических колебаний

Одно из ключевых понятий, связанных с гармоническими колебаниями, - это уравнение гармонических колебаний. Уравнение гармонических колебаний позволяет описать изменение во времени физической величины, подчиняющейся гармоническому закону.
Уравнение гармонических колебаний имеет вид:
| $$x(t) = A \cdot \cos(\omega t + \phi)$$ |
где:
- $$x(t)$$ - значение физической величины в момент времени $$t$$
- $$A$$ - амплитуда колебаний
- $$\omega$$ - угловая частота колебаний
- $$\phi$$ - начальная фаза колебаний
Уравнение гармонических колебаний позволяет определить значение физической величины в любой момент времени. Для этого необходимо знать амплитуду колебаний, угловую частоту и начальную фазу.
Уравнение гармонических колебаний является важным инструментом для анализа и предсказания поведения систем, где происходят гармонические колебания. Оно позволяет определить, например, период, частоту и фазу колебаний.
Временные параметры колебаний
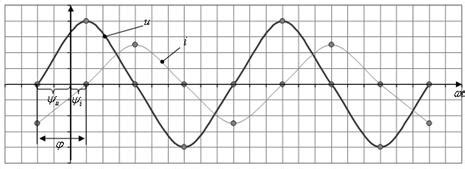
Одним из ключевых временных параметров является период колебаний (T). Он представляет собой время, за которое система выполняет одно полное колебание. Период обратно пропорционален частоте колебаний (f), их количество в единицу времени. Соотношение между периодом и частотой задается формулой: T = 1/f.
Другим важным временным параметром является фаза колебаний (φ). Она определяет текущее состояние системы внутри периода колебаний. Фаза измеряется в радианах или градусах и может принимать значения от 0 до 2π (или от 0 до 360 градусов). Фаза позволяет определить, находится ли система в начальной или конечной точке колебаний, а также в какую сторону происходит движение.
Еще одним важным временным параметром является амплитуда колебаний (A). Она представляет собой максимальное отклонение системы от положения равновесия. Амплитуда определяет, насколько сильными будут колебания. Чем больше амплитуда, тем сильнее колебания.
Знание временных параметров колебаний позволяет более глубоко изучать и анализировать гармонические колебания. Они являются основой для расчетов и прогнозов в различных областях науки и техники.
Способы определения времени колебания

1. Измерение периода
Самым простым и распространенным способом определения времени колебания является измерение периода - времени, через которое происходит одно полное колебание. Для этого необходимо записать время, за которое проходит несколько колебаний и разделить его на количество колебаний.
2. Измерение частоты
Частота колебаний является обратным значением периода и определяется как количество колебаний, совершаемых телом в единицу времени. Измерение частоты также позволяет определить время колебания, поскольку период и частота связаны обратной зависимостью.
3. Использование математических формул
Для сложных систем гармонических колебаний, например, при наличии дополнительных сил или изменении амплитуды, могут использоваться математические формулы для определения времени колебания. В таких случаях необходимо анализировать уравнения движения и использовать соответствующие методы решения.
4. Использование физических экспериментов
Для определения времени колебания может быть использован ряд физических экспериментов, включая использование специальных устройств, таких как секундомеры или осциллографы. Эти методы позволяют получить более точные значения времени колебания и использовать его в более сложных вычислениях или исследованиях.
В зависимости от конкретной задачи или условий определения времени колебания можно выбрать наиболее удобный и точный способ. Комбинирование различных методов также может быть полезным для получения более полной информации о процессе гармонических колебаний.
Методы измерения времени колебаний

- Секундомеры и таймеры
- Осциллографы
- Методы оптического измерения
- Астрономические методы
Для более точного измерения времени колебаний используются осциллографы. Осциллографы позволяют визуализировать колебания на экране и измерять время между точками на графике. С помощью осциллографов можно получить более точные результаты измерений и анализировать форму колебаний.
Оптические методы измерения времени колебаний основаны на использовании световых сигналов. Например, с помощью фотоэлементов можно измерить время между пересечением объектом светового луча. Также существуют специальные датчики, которые регистрируют изменение интенсивности света при колебаниях и позволяют определить время.
Для измерения длительности колебаний с высокой точностью используются астрономические методы. Например, можно определить время колебаний по звездам или другим небесным объектам. Астрономические наблюдения позволяют достичь высокой точности измерений, однако требуют специализированного оборудования и навыков.
Принципы определения периода колебаний
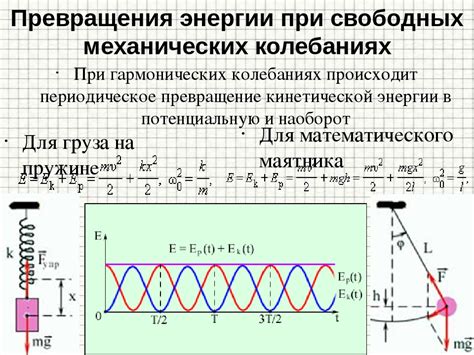
Принцип регулярности
Один из основных принципов определения периода колебаний основывается на предположении о регулярности и повторяемости движения. Согласно этому принципу, период колебаний можно определить путем измерения времени, которое затрачивает точка на прохождение одного полного цикла движения. При этом предполагается, что движение точки является регулярным и повторяемым.
Принцип равенства периодов
Другой принцип, используемый для определения периода колебаний, основывается на предположении о равенстве периодов движения для одинаковых систем. Согласно этому принципу, период колебаний можно определить путем измерения времени, которое затрачивают соседние точки на прохождение одного полного цикла движения. При этом предполагается, что период колебаний отдельной точки такой же, как и период колебаний всей системы.
Принцип математических выкладок
Еще один принцип, применяемый для определения периода колебаний, основывается на математических выкладках и формулах. Согласно этому принципу, период колебаний можно определить путем решения уравнений гармонических колебаний и нахождения времени, за которое точка проходит один полный цикл движения. При этом используется математическая модель, описывающая колебания и взаимодействие параметров системы.
Все эти принципы играют важную роль в определении периода колебаний и позволяют получить точную и достоверную информацию о временных характеристиках гармонических колебаний. Они являются основой для проведения экспериментов и измерений в различных областях физики и науки в целом.
Анализ частоты колебаний
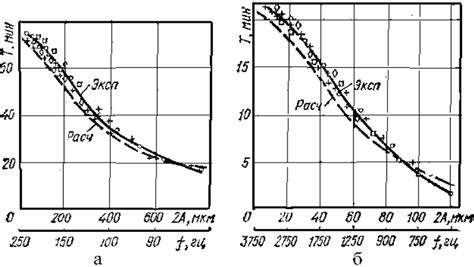
Анализ частоты колебаний позволяет определить, насколько быстро или медленно происходит изменение состояния системы. Высокая частота говорит о быстрых и частых колебаниях, в то время как низкая частота указывает на медленные и редкие колебания.
Частота колебаний может быть представлена в виде уравнения:
f = 1 / T
где f - частота колебаний, а T - период колебаний, то есть время, за которое система выполняет одно полное колебание.
Анализ частоты колебаний позволяет понять, как система реагирует на воздействие внешних сил и какие изменения происходят в ее состоянии в зависимости от времени.
Зависимость времени колебаний от амплитуды
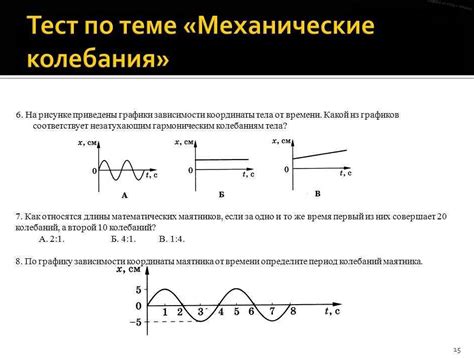
Оказывается, что время колебаний зависит от амплитуды колебаний. Точнее говоря, с увеличением амплитуды колебаний, время одного колебания увеличивается.
Это связано с тем, что при большей амплитуде наибольшая скорость и наибольшая избыточная сила, возникающие на крайних точках колебательного движения, требуют больше времени для прохождения одного полного цикла.
Таким образом, амплитуда и время колебаний являются обратно пропорциональными величинами: чем больше амплитуда, тем дольше время одного колебания.
Знание этой зависимости позволяет более точно определить время колебаний и прогнозировать их характеристики в зависимости от амплитуды колебаний.