Определение высоты цилиндра является важной задачей при решении различных геометрических и инженерных проблем. На практике часто возникает необходимость подсчитать высоту цилиндра, зная только его радиус.
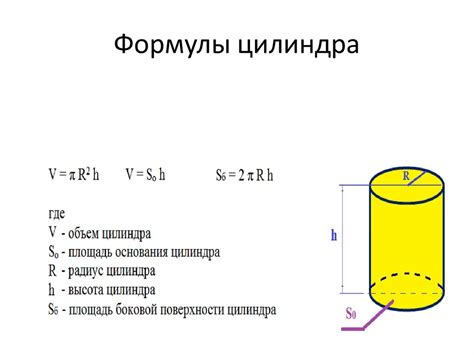
Простой и практичный способ определения высоты цилиндра по его радиусу основан на использовании математической формулы. Известно, что площадь боковой поверхности цилиндра может быть вычислена по формуле S = 2πrh, где S - площадь боковой поверхности, π - число пи (около 3,14), r - радиус цилиндра, h - его высота.
На основе этой формулы можно выразить высоту цилиндра следующим образом: h = S / (2πr). Таким образом, для определения высоты цилиндра по радиусу необходимо знать его площадь боковой поверхности и коэффициент пи (π). При наличии этих данных можно легко определить высоту цилиндра, используя данную математическую формулу.
Формула для расчета высоты цилиндра по радиусу
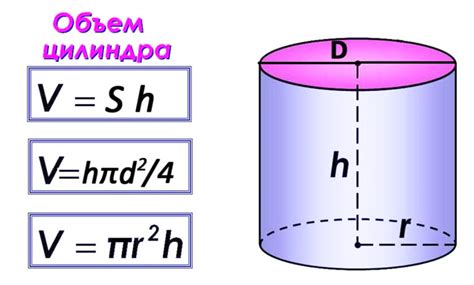
Формула для расчета высоты цилиндра по радиусу выглядит следующим образом:
- Возводим радиус цилиндра в квадрат: r2.
- Умножаем результат на число pi (π), которое приближенно равно 3,14.
- Делим полученное число на площадь основания цилиндра, которая вычисляется по формуле S = πr2.
Результатом будет высота цилиндра. В данном случае важно правильно указать единицы измерения. Например, если радиус цилиндра измерен в метрах, то и высота будет выражена в метрах.
Как использовать формулу для определения высоты цилиндра
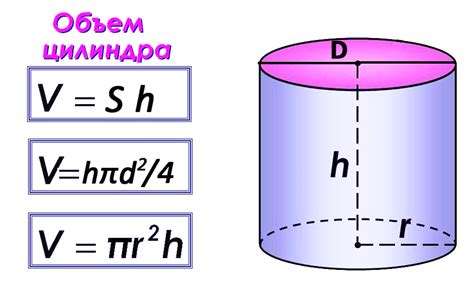
Определение высоты цилиндра по радиусу может быть произведено с помощью простой формулы, которая основывается на геометрии этой фигуры.
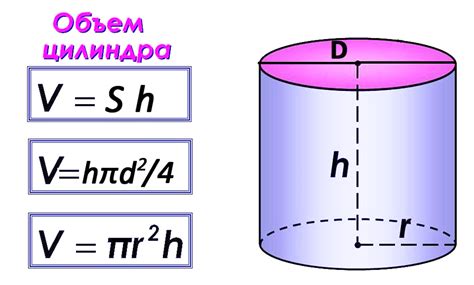
Для определения высоты цилиндра нам понадобится знать радиус основания цилиндра и объем этой геометрической фигуры. Формула для определения высоты цилиндра выглядит следующим образом:
- Высота = объем / (пи * радиус²)
Чтобы понять, как использовать эту формулу, нужно знать, что радиус основания цилиндра измеряется в единицах длины, а объем измеряется в единицах объема. Для проведения вычислений убедитесь, что все единицы измерения согласованы.
Если у вас есть значение радиуса основания цилиндра и объема, просто введите эти значения в формулу и вычислите высоту цилиндра.
Например, предположим, что радиус основания цилиндра равен 5 единицам длины, а объем цилиндра равен 100 единицам объема. Вставляя эти значения в формулу, мы получим:
- Высота = 100 / (3.14159 * 5²)
Выполняя вычисления, мы получим около 1.27 единицы длины как ответ на наш вопрос о высоте цилиндра.
Теперь у вас есть знания и инструменты, чтобы использовать простую формулу для определения высоты цилиндра по радиусу. Этот способ может быть очень полезен в практических ситуациях, таких как строительство или инженерные расчеты.
Преимущества простого способа определения высоты цилиндра
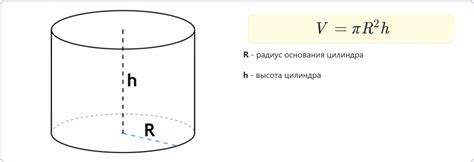
Главным преимуществом данного метода является его простота. Нет необходимости в использовании сложных инструментов или проведении сложных измерений. Достаточно знать только радиус цилиндра и применять соответствующую геометрическую формулу.
Кроме того, простой способ определения высоты цилиндра можно использовать в различных ситуациях. Независимо от того, применяется ли он для расчета объема жидкости в емкости, определения площади поверхности цилиндра или просто для получения информации о его размерах, данный метод работает эффективно и точно.
Еще одним преимуществом простого способа определения высоты цилиндра является его экономичность. Без использования специального оборудования или проведения сложных измерений можно легко и быстро получить необходимую информацию. Это позволяет сэкономить как время, так и ресурсы, что особенно важно в условиях современной динамичной жизни.
Примеры расчета высоты цилиндра по радиусу
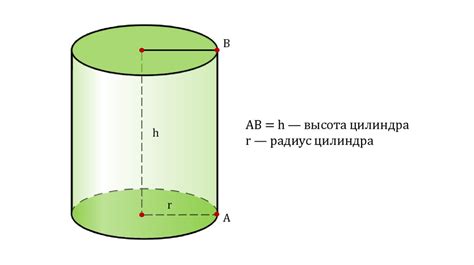
Давайте рассмотрим несколько примеров, чтобы увидеть, как можно использовать формулу для определения высоты цилиндра по его радиусу.
Пример 1:
- Радиус цилиндра: 5 см
- Высота цилиндра: неизвестно
Используя формулу h = V / (π * r^2), где V - объем цилиндра, π - математическая константа (приблизительно равна 3.14159), а r - радиус цилиндра, можно рассчитать высоту следующим образом:
- Подставим значения: h = V / (3.14159 * 5^2)
- Рассчитаем значение для V: V = π * r^2 * h
- Допустим, у нас известен объем цилиндра и он равен 250 см³
- Подставим значения во вторую формулу: 250 = 3.14159 * 5^2 * h
- Рассчитаем значение для h: h = 250 / (3.14159 * 5^2)
- Получаем высоту цилиндра: h ≈ 2.012 см
Пример 2:
- Радиус цилиндра: 8 м
- Высота цилиндра: неизвестно
Используем ту же формулу для рассчета высоты, но уже при других значениях:
- Подставим значения: h = V / (3.14159 * 8^2)
- Допустим, объем цилиндра равен 1120 м³
- Подставим значения во вторую формулу: 1120 = 3.14159 * 8^2 * h
- Рассчитаем значение для h: h = 1120 / (3.14159 * 8^2)
- Получаем высоту цилиндра: h ≈ 4.477 м
Таким образом, с помощью данной формулы можно определить высоту цилиндра по его радиусу, зная объем цилиндра.
Важные указания при использовании формулы для определения высоты цилиндра
1. Величины должны быть указаны в одной системе измерения. Будь то метрическая или английская система, важно, чтобы радиус и высота цилиндра были измерены в одних и тех же единицах.
2. Радиус должен быть точно измерен. Для получения корректных результатов необходимо использовать точные и аккуратные инструменты для измерения радиуса цилиндра. Допускается использование линейки, штангенциркуля или других специализированных инструментов.
3. Используйте правильную формулу. При определении высоты цилиндра по радиусу используется формула Высота = Объем / Площадь основания. Убедитесь, что вы правильно задаете значения радиуса и объема цилиндра, чтобы получить аккуратные вычисления.
4. Проверьте свои расчеты. После того, как вы определите высоту цилиндра по радиусу, всегда стоит проверить свои вычисления. Возьмите изначальные значения и подставьте их обратно в формулу, чтобы убедиться, что получаете те же самые результаты.
Соблюдение данных указаний поможет вам получить точные и надежные значения высоты цилиндра по радиусу, что очень полезно при решении практических задач или выполнении конкретных проектов.
Другие методы определения высоты цилиндра
Один из таких методов основан на измерении угла наклона цилиндра. Для этого необходимо использовать уровень или другое устройство для определения наклона поверхности цилиндра относительно горизонтали. Затем можно использовать геометрическую формулу, чтобы найти высоту, зная радиус и угол наклона.
Еще один метод основан на использовании теодолита или другого инструмента для измерения углов. Для этого необходимо измерить углы, образуемые двумя линиями, проведенными через основание цилиндра. Затем по этим углам можно вычислить высоту цилиндра, используя математические формулы и тригонометрию.
Кроме того, существуют и другие специализированные методы определения высоты цилиндра, которые могут быть применимы в конкретных ситуациях. Например, при использовании лазерных технологий или компьютерного моделирования.
| Метод | Описание |
|---|---|
| Измерение угла наклона | Измерение угла наклона поверхности цилиндра относительно горизонтали и использование геометрической формулы для определения высоты. |
| Измерение углов | Измерение углов, образуемых двумя линиями, проведенными через основание цилиндра, и использование математических формул и тригонометрии для определения высоты. |
| Специализированные методы | Использование лазерных технологий или компьютерного моделирования для определения высоты цилиндра в конкретных ситуациях. |