Определение взаимно простых чисел является фундаментальной задачей в теории чисел. Два числа считаются взаимно простыми, если их наибольший общий делитель (НОД) равен 1. Это означает, что эти числа не имеют общих множителей, кроме единицы.
Понимание и определение взаимно простых чисел имеет большое значение в криптографии, теории кодирования и других областях. Определение наибольшего общего делителя двух чисел является первым шагом в эффективных алгоритмах поиска взаимно простых чисел.
Существуют несколько простых и эффективных способов определения взаимно простых чисел. Один из них основан на алгоритме Евклида, который позволяет найти НОД двух чисел. Если НОД равен 1, то числа взаимно просты. Этот алгоритм имеет линейную временную сложность и является одним из наиболее быстрых способов определения взаимной простоты чисел.
Определение взаимно простых чисел

Взаимно простыми называются два натуральных числа, которые не имеют общих делителей, кроме 1. Определить взаимную простоту двух чисел можно с помощью нескольких простых и эффективных способов.
Для начала необходимо найти все простые делители каждого из чисел. Для этого можно использовать метод факторизации. Затем сравнить найденные делители и проверить, есть ли среди них общие. Если общих делителей нет, то числа взаимно просты.
Также можно воспользоваться алгоритмом Эйлера для определения взаимной простоты двух чисел. Этот алгоритм основан на свойствах функции Эйлера, которая показывает количество натуральных чисел, меньших данного числа и взаимно простых с ним. Если функция Эйлера для двух чисел равна 1, то эти числа взаимно просты.
Таблица может использоваться для более наглядного представления процесса определения взаимной простоты. В первом столбце таблицы указываются числа, для которых ищется взаимная простота. Во втором столбце указываются простые делители каждого числа. В третьем столбце отмечается наличие общих делителей. Если общих делителей нет, то в ячейку ставится знак "+", если есть - знак "-". В четвертом столбце знаком "*" отмечается наличие общих простых делителей.
| Числа | Простые делители | Наличие общих делителей | Наличие общих простых делителей |
|---|---|---|---|
| Число A | p1, p2, ..., pn | + | * |
| Число B | q1, q2, ..., qn | + | * |
Применение таких методов и таблиц упрощает определение взаимной простоты двух чисел и позволяет эффективно выполнять данную задачу.
Понятие взаимно простых чисел
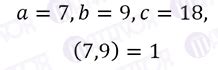
Взаимно простыми числами называются два числа, которые не имеют общих делителей кроме 1. Иными словами, их наибольший общий делитель (НОД) равен 1.
К примеру, числа 4 и 9 являются взаимно простыми, так как их единственный общий делитель равен 1. Однако, числа 8 и 12 не являются взаимно простыми, так как они имеют общий делитель 4.
Понятие взаимно простых чисел является важным в различных областях математики и информатики. Например, для криптографии используется факт, что если два числа являются взаимно простыми, то можно легко найти их обратные элементы в модулярной арифметике.
Существуют различные методы для определения взаимно простых чисел. Один из наиболее эффективных способов - использование алгоритма Евклида для нахождения НОД.
Таким образом, понятие взаимно простых чисел является важным инструментом при решении различных задач и построении различных алгоритмов, и его использование может значительно упростить решение математических и информационных задач.
Простые способы определения взаимно простых чисел

Взаимно простыми числами называются два числа, которые не имеют общих делителей, кроме единицы. Это важное понятие в теории чисел и применяется в различных областях математики, включая криптографию и алгоритмы.
Существует несколько простых способов определения взаимно простых чисел:
- Проверка наличия общих делителей: Для определения, являются ли два числа взаимно простыми, можно проверить, есть ли у них общие делители, кроме единицы. Для этого необходимо разложить числа на простые множители и сравнить их множества. Если у чисел есть общие простые множители, то они не являются взаимно простыми.
- Алгоритм Евклида: Это классический алгоритм, который позволяет эффективно находить наибольший общий делитель двух чисел. Если НОД равен 1, то числа являются взаимно простыми. Алгоритм Евклида можно применять снова и снова, чтобы проверить, взаимно просты ли числа.
- Таблица Эйлера: В таблице Эйлера можно найти количество взаимно простых чисел с заданным числом до него. Если число имеет такое количество взаимно простых чисел, равное его значению минус один, то оно является взаимно простым по отношению к этим числам.
Использование данных способов позволяет быстро и надежно определить, являются ли два числа взаимно простыми. Это полезное знание в математике и может быть применено в различных практических задачах.
Эффективные методы определения взаимно простых чисел

Взаимно простыми числами называются такие числа, у которых наибольший общий делитель равен единице. Определение взаимно простых чисел может быть выполнено несколькими эффективными методами:
- Алгоритм Эвклида: Для определения взаимной простоты двух чисел, можно использовать алгоритм Эвклида. Суть алгоритма заключается в последовательном нахождении остатка от деления одного числа на другое. Если остаток равен нулю, то числа не являются взаимно простыми, иначе нужно продолжить алгоритм с делителем и остатком, полученным на предыдущем шаге. Если последний остаток равен единице, то числа являются взаимно простыми.
- Тест Миллера-Рабина: Для определения взаимной простоты двух больших чисел, можно использовать Тест Миллера-Рабина. Этот тест позволяет проверить, является ли число простым или вероятно простым. Если оба числа проходят тест Миллера-Рабина, то они взаимно простые.
- Разложение на простые множители: Если числа сравнительно маленькие, их можно разложить на простые множители и сравнить полученные разложения. Если ни один простой множитель не повторяется в разложениях обоих чисел, то они будут взаимно простые.
Выбор метода определения взаимно простых чисел зависит от размеров чисел и требований к эффективности и скорости вычислений.