Взаимное расположение прямых в пространстве или на плоскости является одной из основных задач геометрии. Понимание этого понятия позволяет решать множество задач, связанных с анализом пространственных объектов и их взаимодействием.
Существует несколько методов и алгоритмов, позволяющих определить взаимное расположение прямых. Одним из самых популярных методов является использование уравнений прямых. Каждая прямая задается уравнением, которое можно привести к каноническому виду. Затем, сравнивая полученные уравнения, можно определить, пересекаются ли прямые, или же они параллельны и не имеют общих точек.
Другим известным методом является использование векторов. Каждая прямая задается вектором направления. Сравнивая направления прямых, мы можем определить, сонаправлены ли они или же пересекаются под углом. Этот метод особенно эффективен при работе с прямыми в трехмерном пространстве.
Определение взаимного расположения прямых
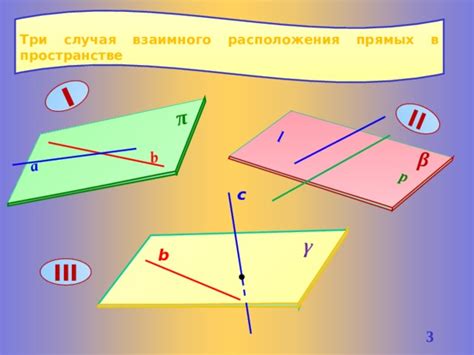
Существуют различные методы и алгоритмы для выполнения этой задачи. Один из наиболее распространенных методов - это использование уравнений прямых и взаимного решения системы линейных уравнений.
Метод уравнений прямых основан на том факте, что каждая прямая на плоскости может быть представлена уравнением вида y = mx + b, где m - наклон прямой, а b - ее смещение по оси y.
Для определения взаимного расположения прямых с помощью данного метода необходимо привести уравнения прямых к стандартной форме и решить систему уравнений. В результате решения системы будут получены значения, которые позволят определить, пересекаются ли прямые, параллельны ли они, или же принадлежат одной и той же прямой.
Кроме метода уравнений прямых, существуют и другие методы определения взаимного расположения прямых, такие как графический метод, метод с использованием углов между прямыми и др.
Выбор метода зависит от конкретной ситуации и поставленной задачи. Расширение знаний о взаимном расположении прямых может быть полезным при решении различных геометрических задач, в том числе при построении графиков функций, нахождении пересечений прямых и других геометрических объектов.
Методы определения взаимного расположения прямых
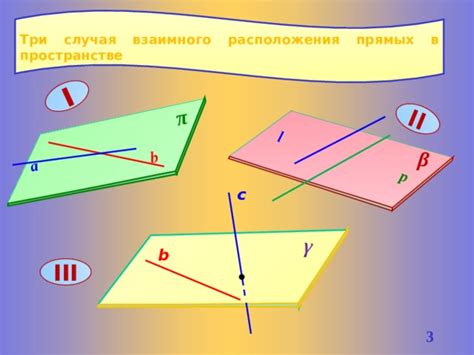
Один из таких методов - метод сравнения углов наклона прямых. В этом методе прямые сравниваются по их углу наклона. Если углы наклона прямых одинаковые, то они параллельны. Если углы наклона противоположные, то прямые пересекаются. Если углы наклона прямых разные, то они скрещиваются.
Еще один метод - метод расчета пересечения прямых. В этом методе находятся координаты точки пересечения прямых. Для этого используются уравнения прямых и системы линейных уравнений. Если систему можно решить, то прямые пересекаются. Если система не имеет решений, то прямые параллельны. Если система имеет бесконечное количество решений, то прямые совпадают.
Также существуют методы определения взаимного расположения прямых с помощью векторного и параметрического уравнений прямых. Эти методы позволяют найти точки пересечения прямых и определить их взаимное расположение.
Выбор метода определения взаимного расположения прямых зависит от задачи и доступных данных. Каждый метод имеет свои преимущества и ограничения. Важно учитывать их при выборе метода для решения конкретной задачи.
Алгоритмы определения взаимного расположения прямых
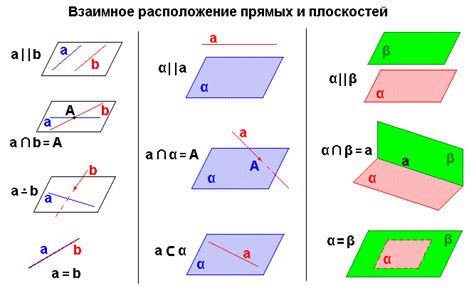
Один из самых простых алгоритмов - это проверка коэффициентов прямых. Коэффициенты наклона и свободного члена позволяют определить, пересекаются ли прямые, параллельны или совпадают. Если у двух прямых одинаковый коэффициент наклона и разные свободные члены, то они параллельны. Если у двух прямых одинаковые коэффициенты наклона и свободные члены, то они совпадают. Если у двух прямых разные коэффициенты наклона, то они пересекаются.
Еще один алгоритм - это определение расположения прямых с использованием пересечения. Если две прямые пересекаются, то у них есть общая точка, координаты которой можно определить. Если общая точка принадлежит обоим прямым, то они пересекаются. Если общая точка находится только на одной из прямых, то они параллельны.
Алгоритмы определения взаимного расположения прямых можно применять как в двумерной, так и в трехмерной геометрии. В трехмерном пространстве алгоритмы становятся более сложными, так как кроме коэффициентов наклона и свободных членов необходимо учитывать еще и направляющие векторы прямых. Однако, основные принципы остаются теми же.