Знание алгебры является основой для понимания и решения множества математических задач. Одной из важных тем в алгебре является решение уравнений. Однако, нередко возникают ситуации, когда заранее не известны значения коэффициентов уравнения. В таких случаях графический метод позволяет определить значения коэффициентов a, b и c по графику.
Для начала, давайте разберемся, что представляет собой график. График уравнения - это геометрическое представление решений этого уравнения. Он позволяет наглядно представить зависимость величин и позволяет найти решение уравнения путем пересечения графика с определенными осями координат.
Теперь перейдем к конкретным шагам и примерам определения значений a, b и c по графику. Начнем с простого примера. Пусть дано квадратное уравнение y = ax^2 + bx + c. Задача состоит в определении значений коэффициентов a, b и c по известному графику этого уравнения.
Для этого мы будем использовать несколько свойств графика. Во-первых, мы знаем, что вершина параболы указывает на значение коэффициента a, так как это определяет направление открытия параболы. Во-вторых, мы можем использовать точку пересечения графика с осью ординат (y-осью) для определения значения коэффициента c. И, в-третьих, точки пересечения графика с осью абсцисс (x-осью) позволяют определить значение коэффициента b.
Определение значений a, b и c по графику
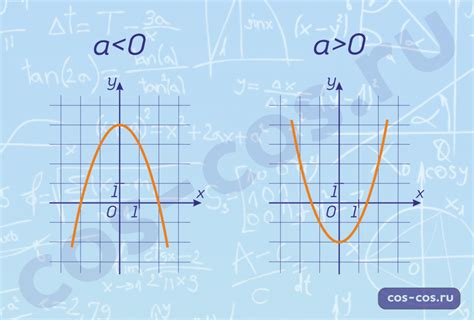
График функции вида y = a*x^2 + b*x + c представляет собой параболу. Чтобы определить значения коэффициентов a, b и c, необходимо иметь достаточно информации о графике и его характеристиках.
Коэффициент a определяет, как "открыта" парабола: она будет направлена вниз (a < 0) или вверх (a > 0). Если a = 0, то это уже не парабола, а линейная функция y = b*x + c.
Коэффициент c отвечает за смещение параболы по вертикальной оси (ось y). Если c > 0, то парабола будет поднята вверх относительно начала координат, а если c < 0, то парабола опущена вниз.
Коэффициент b определяет смещение параболы по горизонтальной оси (ось x). Чем больше значение b, тем сильнее парабола будет наклонена вправо (b > 0) или влево (b < 0).
Для определения значений a, b и c можно использовать информацию о вершинах параболы, пересечении с осями координат, а также дополнительные точки графика.
Например, если известны координаты вершины параболы (x0, y0) и хотя бы одна дополнительная точка на графике, можно составить систему уравнений и решить ее, чтобы найти значения a, b и c.
Примеры и инструкция

Чтобы определить значения a, b и c по графику, следуйте указанным ниже шагам:
- Изучите график, представленный на оси координат.
- Определите точки пересечения графика с осями координат.
- Если график пересекает ось X в точке (a,0), то значение a будет равно x-координате точки.
- Если график пересекает ось Y в точке (0,b), то значение b будет равно y-координате точки.
- Определите вершину параболы, если график представляет собой параболу. Вершина параболы является экстремальной точкой и находится на равном удалении от обеих ветвей параболы.
- Если вершина параболы имеет координаты (a, c), то значение a будет равно x-координате вершины, а значение c будет равно y-координате вершины.
- Если парабола открыта вниз, значит, значение c будет отрицательным.
- Если парабола открыта вверх, значит, значение c будет положительным.
- Запишите полученные значения a, b и c.
Вот пример решения задачи:
- График пересекает ось X в точке (3, 0).
- График пересекает ось Y в точке (0, -2).
- Вершина параболы имеет координаты (1, -4).
- Значения a, b и c равны: a = 3, b = -2, c = -4.
Как определить значения a, b и c
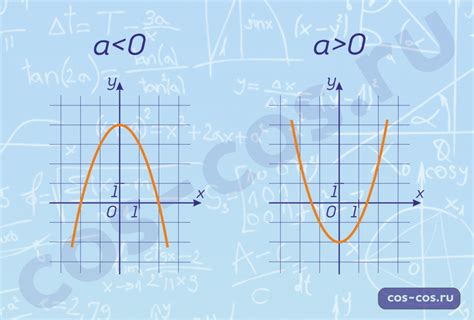
Для начала нужно заметить, что график функции иногда может подсказать нам значения переменных a, b и c.
Если функция представляет собой параболу, то мы можем сказать некоторые вещи о значениях переменных. Если парабола направлена вверх, то a должно быть положительным числом. Если парабола направлена вниз, то a должно быть отрицательным числом.
Зная вершину параболы, которая представляет собой точку на графике, мы можем определить значение b. Если вершина находится в точке (h, k), то b = k.
Также нам пригодится знание о том, как влияют на график значения a, b и c. Значение a определяет ширину параболы: если a близко к нулю, то парабола будет широкой, а если a большое число, то парабола будет узкой. Значение c определяет положение параболы по вертикальной оси: если c положительное число, то парабола будет смещена вверх, если c отрицательное число, то парабола будет смещена вниз.
В таблице ниже приведены примеры определения значений a, b и c по графикам функций.
| График функции | Значение a | Значение b | Значение c |
|---|---|---|---|
 | 3 | 2 | -1 |
 | -2 | -1 | 3 |
 | 1 | 0 | 0 |
Используя график функции, мы можем определить значения a, b и c, что дает нам более полное представление об уравнении или неравенстве.
Примеры использования графика для определения значений
Графики могут быть очень полезны для определения значений переменных или параметров в различных задачах и ситуациях. Ниже приведены несколько примеров, которые иллюстрируют, как графики могут помочь в определении значений переменных a, b и c.
Пример 1:
Допустим, у нас есть квадратное уравнение вида: ax^2 + bx + c = 0. Мы могли бы построить график этого уравнения и проанализировать его форму и свойства. Например, если график имеет вершину в точке (1, 4) и проходит через точку (2, 2), мы можем заключить, что a = 1, b = -4 и c = 3. Таким образом, график помогает нам определить значения переменных.
Пример 2:
Рассмотрим задачу о движении тела с постоянным ускорением. Ускорение a и начальная скорость v0 известны, и мы хотим найти скорость v и перемещение x в заданный момент времени t. Мы можем построить графики скорости и перемещения относительно времени и использовать их для определения значений переменных. Например, если график скорости представляет собой прямую линию, мы можем заключить, что a = 0 и v0 = 2 м/с. Тогда, используя график перемещения, мы можем определить значение переменной x в заданный момент времени t.
Пример 3:
В задачах связанных с процессом роста и распада вещества, графики могут использоваться для определения значений параметров. Например, если график экспоненциального роста представляет собой ветвь параболы, мы можем вычислить коэффициенты a, b и c, используя известные точки на графике. Эти значения позволят нам описать процесс роста или распада в математической форме и делать прогнозы или принимать решения на основе этих значений.