При изучении экстремумов многих функций часто возникает вопрос: как определить их тип? Ведь важно не только найти точку максимума или минимума, но и понять, является ли она локальной или глобальной.
Одним из эффективных методов определения типа экстремума является использование миноров. Минор это определитель квадратной подматрицы матрицы Гессе в окрестности точки экстремума. От значения минора зависит тип экстремума: если минор положителен, то точка экстремума - это локальный минимум, если минор отрицателен - локальный максимум, если же минор равен нулю, то точка экстремума может быть или точкой минимума с горизонтальной касательной, или точкой максимума с горизонтальной касательной.
Чтобы определить тип экстремума с помощью миноров, необходимо вычислить все миноры матрицы Гессе и проанализировать их значения. Если все миноры положительны или все миноры отрицательны, то точка экстремума будет глобальной. Если среди миноров есть нулевой минор, то точку экстремума нужно анализировать подробнее с помощью других методов.
Что такое тип экстремума
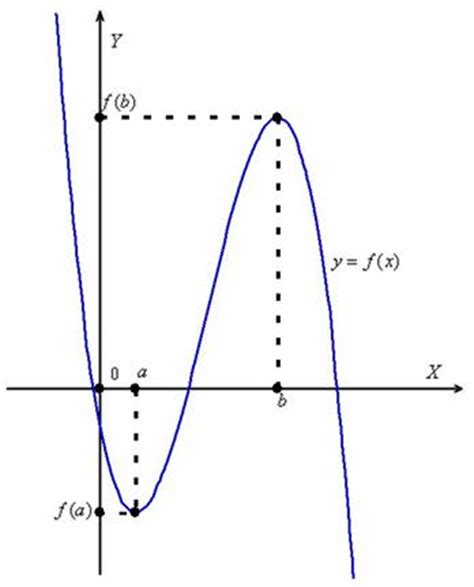
Если первая производная функции равна нулю в точке экстремума, то можно сделать предположение о его типе, основываясь на знаке второй производной:
| Знак второй производной | Тип экстремума |
|---|---|
| Положительный | Точка минимума |
| Отрицательный | Точка максимума |
Признаки максимума

Для определения типа экстремума, в данном случае максимума, необходимо обратить внимание на следующие признаки:
1. Локальный максимум. Если значения минора первого порядка равны нулю, а значение минора второго порядка отлично от нуля и положительно, то это указывает на наличие локального максимума.
2. Глобальный максимум. Если значения всех миноров первого порядка равны нулю, значениях миноров второго порядка положительны и первый минор третьего порядка отрицателен, то это указывает на наличие глобального максимума.
3. Контактный максимум. Если значения всех миноров первого порядка равны нулю, а значениях всех миноров второго порядка равны нулю и первый минор третьего порядка равен нулю, то это указывает на наличие контактного максимума.
Используя эти признаки, можно определить тип экстремума по минорам и установить, является ли точка максимумом.
Признаки минимума

Однако стоит учесть, что наличие этих признаков не гарантирует наличие минимума. Возможны случаи, когда точка не является экстремумом или имеет точки перегиба, где функция может быть строго монотонной.
Как определить точку перегиба
Чтобы найти точку перегиба, следуйте следующим шагам:
- Найдите вторую производную функции. Для этого возьмите первую производную и продифференцируйте ее еще раз.
- Решите уравнение второй производной функции равное нулю. Это уравнение поможет найти точки, в которых вторая производная равна нулю или не существует.
- Найдите вторую производную отрицательную справа от найденных точек и положительную слева от них. Точки, в которых меняется знак второй производной, будут точками перегиба.
Используя описанные выше методы, вы сможете определить точки перегиба функции и локализовать их на графике. Это позволит более точно исследовать поведение функции в окрестности этих точек, а также использовать их в решении задач и оптимизационных проблем.
Глобальный максимум и минимум
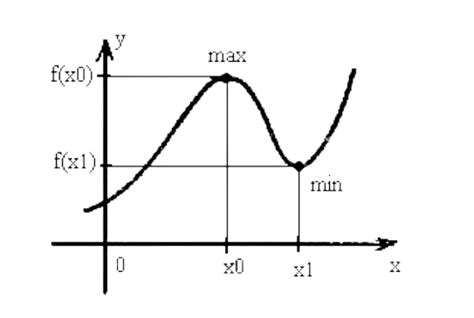
Глобальный максимум функции - это наибольшее значение функции на всем ее области определения. Иными словами, это точка, в которой значение функции выше, чем во всех остальных точках.
Наибольшую точку функции можно определить путем сравнения значений функции во всех стационарных точках (где производная равна нулю) и на границах области определения функции. Глобальный максимум может быть только один.
Глобальный минимум функции - это наименьшее значение функции на всем ее области определения. Иными словами, это точка, в которой значение функции ниже, чем во всех остальных точках.
Наименьшую точку функции можно определить также путем сравнения значений функции во всех стационарных точках и на границах области определения функции. Глобальный минимум также может быть только один.
Глобальные максимум и минимум имеют важное значение при решении оптимизационных задач. Их нахождение позволяет нам найти значения функции, которые максимизируют или минимизируют некий критерий.
Частные максимумы и минимумы
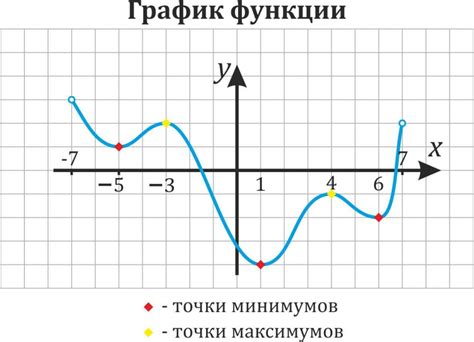
При исследовании функции нескольких переменных с помощью миноров, мы можем определить наличие точек экстремума. Если определитель минора равен нулю, то имеется точка поверхности, в которой функция имеет экстремум. Если определитель минора отрицательный или положительный, то функция имеет максимум или минимум соответственно. Однако в случае функции нескольких переменных важно проанализировать не только сам минор, но и все его подмножества. Знаки определителей этих подмножеств помогут определить тип экстремума в данной точке.
Частные максимумы и минимумы могут быть как локальными, для конкретной точки, так и глобальными, для всей функции. Для определения глобального экстремума необходимо проанализировать все точки экстремума функции. Локальный же экстремум может быть достаточно непредсказуемым и зависит от специфики задачи.
При анализе частных максимумов и минимумов важно учитывать геометрическое представление функции нескольких переменных. Вектор градиента позволит определить направление наискорейшего возрастания или убывания фунцкции в заданной точке. Комбинация градиента и миноров дает возможность определить тип экстремума в данной точке и объяснить его поведение.
Экстремумы и производные

Производная функции – это функция, которая показывает изменение значения функции при изменении аргумента. Производная может быть положительной, отрицательной или равной нулю.
Если производная положительна на интервале слева от точки экстремума и отрицательна на интервале справа, то точка экстремума является максимумом. Если производная отрицательна на интервале слева от точки экстремума и положительна на интервале справа, то точка экстремума является минимумом.
Если производная равна нулю в точке экстремума, то она является стационарной точкой. Однако, это не всегда означает наличие экстремума в данной точке. Для дальнейшего анализа необходимо изучить значения производной в окрестности этой точки.
Кроме того, существуют случаи, когда функция не имеет экстремума. Например, это может быть случай функции с ростом или убыванием на всей области определения, или функции с точками разрыва.
Как применить миноры для определения типа экстремума
Миноры - это определители, которые строятся на основе вторых производных функции. Они позволяют анализировать поведение функции в окрестности точки экстремума и определить его тип.
Применение миноров для определения типа экстремума происходит следующим образом:
1. Необходимо вычислить все частные производные функции до второго порядка. Для этого используются правила дифференцирования и методы нахождения производных сложных функций.
2. Построить матрицу Гессе, которая состоит из вторых производных функции по каждой паре переменных. В матрице Гессе элементы находятся путем взятия частных производных второго порядка.
3. Вычислить определитель матрицы Гессе. Если определитель положителен, то точка является локальным минимумом, если отрицателен - локальным максимумом. Если определитель равен нулю, то метод не дает однозначного результата.
4. Дополнительно можно проанализировать значения внутренних минорных детерминантов матрицы Гессе. Они позволяют определить тип седловой точки или точки перегиба.
| Тип экстремума | Определитель матрицы Гессе | Внутренние миноры | Тип точки |
|---|---|---|---|
| Локальный минимум | Положительный | Все положительные | Минимум |
| Локальный максимум | Отрицательный | Чередуются положительные и отрицательные | Максимум |
| Седловая точка | Отрицательный | Все отрицательные и положительные | Седло |
| Точка перегиба | Нулевой | Различные | Перегиб |
Таким образом, применение миноров позволяет определить тип экстремума функции и проанализировать ее поведение вблизи точки экстремума. Это важный инструмент для решения задач оптимизации и анализа математических моделей.