Синус – это одна из основных тригонометрических функций, играющая важную роль в математике и физике. Она определяется отношением длины противолежащего катета треугольника к длине гипотенузы. Значение синуса угла варьируется от -1 до 1 в радианах или градусах, и он используется для решения множества задач, связанных с расчетами и построением графиков.
Синус угла имеет большое значение в физике, где он позволяет определить равномерное движение и гармонические колебания. Например, при изучении колебаний механической системы с помощью синусоидальной функции, синус угла определяет периодичность и амплитуду колебаний. Значение синуса также применяется при анализе волновых процессов и электромагнитных колебаний.
В прикладной физике синус угла широко используется в различных областях, таких как механика, астрономия, акустика и оптика. Он позволяет определить фазовые переходы, резонансные явления и интерференцию световых волн. Также синус угла находит применение в электронике, в особенности при проектировании сигнальных схем и фильтров.
Определение синуса угла

Для определения синуса угла необходимо знать длины сторон прямоугольного треугольника. Зная длину противолежащего катета и гипотенузы, можно вычислить синус угла по формуле sin = (противолежащий катет) / (гипотенуза).
Значение синуса угла имеет важное значение в различных областях науки и физики. Например, в механике для определения сил, которые действуют на тела при движении вокруг оси. В электрических цепях синус угла используется для определения фазового сдвига между током и напряжением. Также синус угла широко применяется в геодезии и астрономии для определения расстояний и углов между небесными телами.
Что такое синус и как его определить
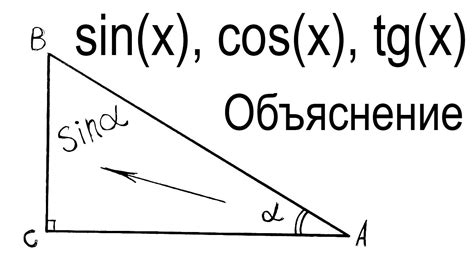
Для определения значения синуса угла, сначала необходимо определить соответствующий треугольник. Затем, измерить длину противоположной стороны к углу и гипотенузы. Деление этих двух величин даст значение синуса угла.
Синус угла широко применяется в физике для анализа колебаний, волн, осцилляций и других процессов, где величины изменяются периодически во времени. В механике, электронике и других областях физики синус играет важную роль при описании и анализе размеров и пропорций объектов, углов и дистанций.
Как использовать таблицу синусов для определения значения

Таблица синусов представляет собой удобный инструмент, который позволяет быстро и легко определить значение синуса угла. Таблица содержит углы от 0 до 90 градусов и соответствующие им значения синуса.
Для использования таблицы синусов, необходимо найти в таблице значение синуса, соответствующее данному углу. Например, если угол равен 30 градусам, нужно найти значение синуса для угла 30° в таблице. По соответствующему значению в таблице можно определить значение синуса угла.
Таблица синусов также может быть использована для нахождения угла по заданному значению синуса. Для этого нужно найти в таблице значение синуса, ближайшее к заданному, и определить соответствующий угол.
Использование таблицы синусов позволяет избежать необходимости выполнять сложные математические вычисления и сократить время на определение значения синуса угла.
Применение графика синуса для нахождения значения

С помощью графика синуса можно определить значение синуса угла, если известно значение самого угла. Для этого необходимо на графике найти точку с заданным значением угла на оси абсцисс и провести вертикальную линию до графика синуса. Затем следует определить значение синуса, которое соответствует найденной точке на графике. Таким образом, график синуса позволяет найти значение синуса угла без использования специальных таблиц или калькуляторов.
Применение графика синуса находит широкое применение в физике. Например, при решении задач на механику его использование позволяет определить силы, действующие при движении тела под углом к горизонту, учитывая значение синуса угла наклона. Также график синуса используется при анализе колебательных процессов, волновых явлений и других физических явлений, где синус угла играет важную роль.
Роль синуса в физике
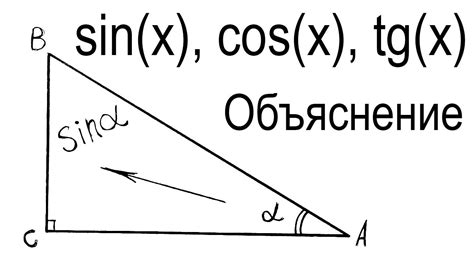
В физике синус играет важную роль при решении задач, связанных с движением, колебаниями и волнами. Например, в акустике синус используется для описания звуковых волн, в оптике - для расчета углов преломления и отражения света, а в механике - для определения гармонического движения.
Основное значение синуса заключается в его связи с периодическими функциями и колебаниями. Синусоидальные колебания широко распространены в физике и естественных явлениях. Например, электрические сигналы в виде синусоидальных волн используются в телекоммуникационных системах и электронике.
Кроме того, синус применяется при анализе и моделировании электрических цепей, определении активной и реактивной составляющих тока и напряжения, а также при решении задач с механическими и электромагнитными волнами.
Таким образом, роль синуса в физике несомненно важна. Его значение и свойства помогают ученым и инженерам понять и описать физические явления, решить сложные задачи и разработать новые технологии.
Связь между синусом и колебаниями

Колебания могут быть представлены в виде гармонических функций, которые описываются с помощью синуса или косинуса. Синус является основной функцией при описании гармонических колебаний, так как он представляет собой график синусоидальной формы.
Синус имеет периодическую природу, что делает его идеальным для описания колебаний, которые повторяются через определенное время. Значение синуса угла изменяется от -1 до 1, что соответствует изменению физической величины во времени. Максимальное значение синуса достигается, когда угол равен 90 градусам или \(\frac{\pi}{2}\) радиан.
Колебания, описываемые синусом, могут быть механическими, электрическими, магнитными и другими. Например, когда материальная точка находится на пружине и подвергается силе восстанавливающей силы, она будет колебаться с определенной амплитудой и частотой. Эти колебания будут иметь синусоидальную форму, которая может быть описана с помощью синусной функции.
Синус имеет важное значение в физике, так как он позволяет совместить математическое описание колебаний с реальными физическими процессами. Он помогает в анализе и предсказании свойств колебательных систем, и его значение можно найти во множестве физических уравнений и законов.
Как синус используется в решении задач динамики

В задачах динамики, сила, направленная под углом к горизонту, может быть разложена на две компоненты - горизонтальную и вертикальную. Горизонтальная компонента силы не влияет на движение тела в вертикальной плоскости, в то время как вертикальная компонента отвечает за вертикальное движение.
Для определения вертикальной компоненты силы используется значение синуса угла между направлением силы и горизонтом. Это можно выразить с помощью следующей формулы:
| Угол | Синус угла |
|---|---|
| 0° | 0 |
| 30° | 0.5 |
| 45° | 0.7071 |
| 60° | 0.866 |
| 90° | 1 |
Таким образом, синус угла позволяет определить величину вертикальной компоненты силы и участвует в решении задач динамики связанных с вертикальным движением тела. Множество задач, таких как бросок камня, падение свободного тела и т. д., могут быть решены с использованием этой функции.
Влияние синуса на изучение акустических явлений

Акустика - это наука об изучении звуковых волн и различных акустических явлений. Синус, как функция, позволяет описывать колебательные процессы, которые возникают в результате звуковых колебаний.
Одной из основных характеристик звука является его частота, которая измеряется в герцах. Частота определяет число колебаний, которое происходит за единицу времени. Синусоидальная функция, в частности синус, может быть использована для математического описания звуковой волны, где частота определяет периодичность колебаний.
Синус также позволяет нам понять феномен интерференции звуковых волн. Интерференция - это явление, при котором две или более звуковых волн взаимодействуют друг с другом. С помощью синуса мы можем описывать амплитудные изменения и фазовые сдвиги, которые возникают при интерференции.
Кроме того, синус имеет широкое применение при анализе звуковых спектров. Звуковой спектр - это разложение акустического сигнала на составляющие гармонические частоты. Синусоидальные функции помогают представить каждую компоненту спектра, что позволяет нам анализировать и изучать акустические явления более подробно и точно.
Таким образом, синус является важным инструментом для изучения акустических явлений. Его использование позволяет описывать звуковые волны, интерференцию, спектры и другие акустические явления с помощью математических моделей и анализа.