Треугольник – это геометрическая фигура, состоящая из трех сторон и углов. Для полного описания треугольника необходимо знать его три стороны, но иногда известны лишь две из них. В этом случае возникает необходимость нахождения третьей стороны, которая называется основанием треугольника.
В геометрии существует несколько способов нахождения основания треугольника при известных двух сторонах. Один из самых простых и понятных способов – используя теорему Пифагора. Если известны длины двух сторон треугольника, то длина основания треугольника можно найти, применив формулу, основанную на этой теореме.
Формула нахождения основания треугольника при известных двух сторонах выглядит следующим образом: основание = √(сторона₁² - сторона₂²). Здесь сторона₁ и сторона₂ - это длины известных двух сторон треугольника. Таким образом, простым подставлением в эту формулу известных значений сторон можно получить длину основания треугольника.
Формула нахождения основания треугольника при известных двух сторонах
Если известны длины двух сторон треугольника и угол между ними, можно использовать формулу для нахождения основания. Для этого нужно воспользоваться теоремой косинусов, которая гласит:
c^2 = a^2 + b^2 - 2ab*cos(C),
где c - длина основания, a и b - длины других двух сторон треугольника, C - угол между ними. Подставляя известные значения в эту формулу и решая ее относительно c, можно найти длину основания.
Если известны длины двух сторон треугольника и высота, опущенная на основание, можно использовать следующую формулу:
c = 2*(S/h),
где c - длина основания, S - площадь треугольника, h - высота, опущенная на основание. Подставляя известные значения в эту формулу, можно найти длину основания.
Зная две стороны треугольника и радиус описанной окружности, можно воспользоваться следующей формулой:
c = 2*R*sin(A)*sin(B)/sin(A+B),
где c - длина основания, R - радиус описанной окружности, A и B - углы при основании. Подставляя известные значения в эту формулу и решая ее относительно c, можно найти длину основания.
Степень
Остроугольный треугольник имеет все три угла меньше 90 градусов. Тупоугольный треугольник имеет один угол больше 90 градусов. Прямоугольный треугольник имеет один угол равный 90 градусов.
Степень треугольника можно вычислить с помощью теоремы косинусов. Для этого необходимо знать длины всех трех сторон треугольника. Используя формулу, можно найти значение степени треугольника.
Равнобедренный треугольник
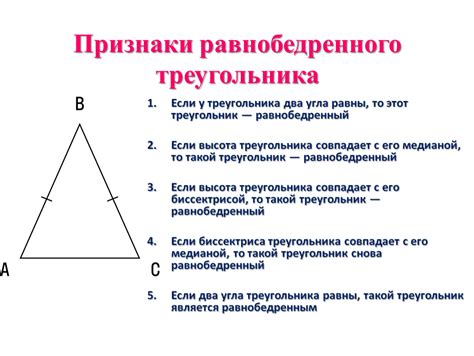
Чтобы найти длину основания равнобедренного треугольника, можно использовать следующую формулу:
b = (a + a) / 2
Где b – длина основания, a – длина равных сторон.
Также можно найти длину основания, используя теорему Пифагора. Предположим, что известны длины двух равных сторон равнобедренного треугольника. Обозначим их как a. Тогда длину основания можно найти по формуле:
b = √(2 * a2 - c2)
Где b – длина основания, a – длина равных сторон, c – длина третьей стороны.
Зная длину равных сторон, можно найти площадь равнобедренного треугольника, используя формулу:
S = (b * h) / 2
Где S – площадь, b – длина основания, h – высота, опущенная на основание.
Если заданы все стороны

Когда известны все три стороны треугольника, возможно использовать формулу для нахождения основания. Для этого необходимо использовать формулу полупериметра, которая вычисляет сумму длин всех сторон и делит результат на 2:
Полупериметр (p) = (a + b + c) / 2
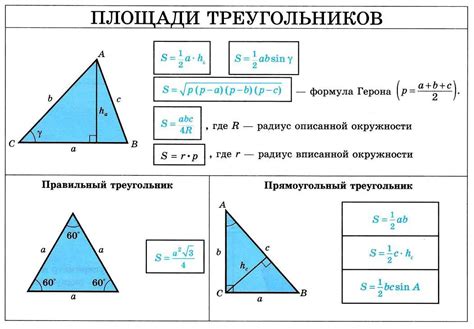
Затем можно воспользоваться формулой Герона для нахождения площади треугольника:
Площадь (S) = sqrt(p * (p - a) * (p - b) * (p - c))
Где a, b и c - длины сторон треугольника.
После нахождения площади, основание треугольника можно вычислить используя следующую формулу:
Основание (b) = (2 * S) / a
Таким образом, зная все три стороны треугольника, можно легко определить его основание, используя формулы полупериметра, площади и основания.
Квадрат разности

Основание треугольника = (сторона1^2 - сторона2^2) / (2 * высота)
Данная формула позволяет находить основание треугольника при известных значениях двух сторон и высоты. Использование "квадрата разности" особенно полезно в случаях, когда нам известны две стороны треугольника и высота, а требуется найти еще одну сторону.
Применение данной формулы требует знания значения двух сторон и высоты в задаче. После подстановки известных значений в формулу, можно рассчитать основание треугольника. Это позволяет определить полный набор значений для данного треугольника и использовать полученные результаты в решении дальнейших задач, связанных с этим треугольником.
Теорема косинусов
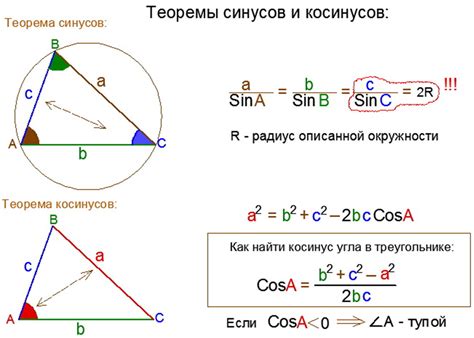
Теорема утверждает, что квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус их общего угла:
a² = b² + c² - 2bc · cos(A)
где a - основание треугольника, b и c - две известные стороны, A - угол между ними.
Используя теорему косинусов, можно находить основание треугольника, если известны две стороны и угол между ними, а также находить угол треугольника, если известны все три стороны.
Данная теорема является мощным инструментом в геометрии и находит применение как в плоской, так и в пространственной геометрии.
Сумма квадратов

Сумма квадратов двух катетов прямоугольного треугольника равна квадрату его гипотенузы. Данное утверждение известно как теорема Пифагора.
Теорема Пифагора формулируется следующим образом:
- Пусть a и b - длины катетов, c - длина гипотенузы прямоугольного треугольника.
- Тогда справедливо следующее равенство: a2 + b2 = c2.
Теорему Пифагора можно использовать для нахождения длины одной из сторон прямоугольного треугольника при известной длине двух других сторон.
Применение теоремы Пифагора особенно полезно в сферах, связанных с геометрией и физикой, таких как архитектура, инженерные расчеты и астрономия.
Полупериметр и радиус вписанной окружности

Радиус вписанной окружности - это радиус окружности, которая проходит через вершины треугольника и касается всех его сторон. Обозначается как r. Радиус вписанной окружности можно найти по формуле: r = √((p−a)⋅(p−b)⋅(p−c) / p), где p - полупериметр треугольника, а a, b и c - длины его сторон.
Знание полупериметра и радиуса вписанной окружности может быть полезно при решении различных геометрических задач. Например, с их помощью можно найти длины сторон треугольника, если известен полупериметр и радиус вписанной окружности. Также эти значения могут использоваться при расчете других характеристик треугольника, например, его площади.
Радиус описанной окружности и площадь треугольника

Для начала, разберемся, что такое радиус описанной окружности. Это радиус окружности, которая проходит через все вершины треугольника. Радиус описанной окружности часто обозначается буквой R.
Для треугольника с известной основанием и высотой, радиус описанной окружности можно вычислить с помощью следующей формулы:
R = (сторона треугольника) / (2 *sin(угол при вершине))
Где угол при вершине - это угол между основанием треугольника и стороной, которая равна радиусу описанной окружности.
Чтобы найти площадь треугольника по известной основе и высоте, используется формула:
Площадь = (основание * высота) / 2
Таким образом, имея величину основания и высоты треугольника, можно легко вычислить радиус описанной окружности и площадь треугольника.