Эллипс - это геометрическая фигура, которая представляет собой закрытую кривую линию, состоящую из всех точек плоскости, для которых сумма расстояний от двух фокусов постоянна. Длина окружности эллипса является одним из основных параметров этой фигуры и может быть определена с использованием некоторых математических формул.
Если оси эллипса имеют длины a и b, где a - большая полуось, а b - меньшая полуось, то длина окружности эллипса может быть вычислена по формуле:
L = π * (3(a + b) - √((3a + b) * (a + 3b)))
Где π (пи) - это математическая константа, приблизительно равная 3,14159. Эта формула позволяет точно определить длину окружности эллипса, основываясь на его размерах.
Определение длины окружности эллипса может быть полезно во многих областях, включая геометрию, физику, строительство и дизайн. Зная длину окружности, можно более точно рассчитать площадь эллипса и выполнить другие расчеты, связанные с его параметрами.
Математическая формула вычисления длины окружности эллипса

Длина окружности эллипса может быть вычислена при помощи следующей формулы:
| Длина окружности эллипса: | L = 2π (a + b) ∫0 π/2 (sin2(θ) / ((a cos(θ))2 + (b sin(θ))2)0.5) dθ |
Где:
- L - длина окружности эллипса
- π - математическая константа, приближенное значение которой равно 3.14159
- a - большая полуось эллипса
- b - малая полуось эллипса
- θ - переменная угла, в пределах от 0 до π/2
Эта формула представляет собой интеграл для определения длины окружности эллипса посредством интегрирования от угла 0 до π/2 и вычисления значения синуса, косинуса и квадратных корней.
Используя данную формулу, можно вычислить точное значение длины окружности эллипса с заданными значениями полуосей a и b.
Что такое эллипс
Эллипс является основой для многих математических и физических разработок. В геометрии эллипс используется для описания орбит планет и спутников, а в оптике - для построения линз и других оптических систем.
Форма эллипса может быть определена с помощью специального параметра, называемого эксцентриситетом. Эксцентриситет равен отношению расстояния между фокусами к длине большой оси. Если эксцентриситет равен нулю, то эллипс превращается в окружность.
Изучение эллипсов позволяет анализировать их длину, площадь и другие характеристики. Например, длина окружности эллипса может быть рассчитана с использованием специальной формулы, которая учитывает величину осей и эксцентриситет.
Основные понятия
Перед тем, как вычислять длину окружности эллипса, важно понять следующие основные понятия:
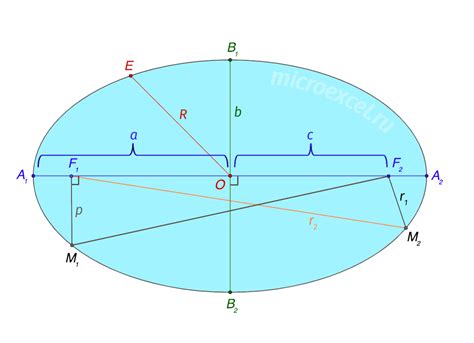
- Эллипс: геометрическая фигура, получающаяся при пересечении плоскости и конуса, когда плоскость не параллельна основанию конуса. Эллипс имеет две фокусные точки и характеризуется полуосью a и полуосью b.
- Фокусные точки: две точки внутри эллипса, для которых сумма расстояний до любой точки на эллипсе всегда одинакова. Фокусные точки обозначаются буквами F1 и F2.
- Большая ось: отрезок, проходящий через две противоположные вершины эллипса и проходящий через центр эллипса. Длина большой оси обозначается как 2a.
- Малая ось: отрезок, проходящий через две противоположные вершины эллипса и перпендикулярный большой оси. Длина малой оси обозначается как 2b.
- Эксцентриситет: параметр, который характеризует степень отклонения эллипса от круга. Эксцентриситет обозначается как е и всегда лежит в интервале от 0 до 1, где е = √(1 - (b^2 / a^2)).
Понимание этих основных понятий позволит более точно и эффективно вычислить длину окружности эллипса. Далее мы рассмотрим алгоритм этого вычисления подробнее.
Формула вычисления длины окружности эллипса

Длина окружности эллипса может быть вычислена с помощью специальной формулы, разработанной математиками. Данная формула основана на радиусах эллипса и эксцентриситете эллипса.
Формула вычисления длины окружности эллипса выглядит следующим образом:
Длина окружности эллипса = 2π * sqrt((a^2 + b^2)/2)
Где π (пи) - математическая константа, равная приблизительно 3,14159. a и b - полуоси эллипса, а sqrt - функция, вычисляющая квадратный корень.
Таким образом, для вычисления длины окружности эллипса необходимо знать значения полуосей a и b. Подставив их в формулу, можно получить точное значение или приближенное значение длины окружности.
Пример вычисления длины окружности эллипса
Длина окружности эллипса:
C = 2π * sqrt((a2 + b2) / 2)
Где:
- C - длина окружности эллипса;
- π - математическая константа, примерно равная 3.14159;
- a - большая полуось эллипса;
- b - малая полуось эллипса.
Например, если большая полуось эллипса равна 5, а малая полуось равна 3, то мы можем использовать формулу для вычисления длины окружности:
C = 2π * sqrt((52 + 32) / 2) = 2π * sqrt(34 / 2) ≈ 2π * sqrt(17) ≈ 6 * 4.123 ≈ 24.738
Таким образом, длина окружности эллипса с большой полуосью 5 и малой полуосью 3 примерно равна 24.738.