Геометрия – это одна из старейших наук, которая изучает пространственные формы, фигуры и их свойства. Важным аспектом геометрии являются теоремы, которые позволяют решать различные задачи и находить закономерности. Одной из самых известных теорем является теорема Пифагора.
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Это правило находит широкое применение в различных областях – от архитектуры до физики. Однако, чтобы правильно применять теорему Пифагора, необходимо знать правила знаков, которые описывают соотношения между сторонами треугольника.
Первое правило знаков в теореме Пифагора гласит, что длины сторон треугольника всегда положительны. Это значит, что ни одна из сторон не может иметь отрицательную длину. Данное правило следует учитывать при использовании теоремы Пифагора для решения задач и нахождения неизвестных сторон треугольника.
Основы геометрии: теорема Пифагора

Согласно этой теореме, квадрат гипотенузы (стороны прямоугольного треугольника, противоположной прямому углу) равен сумме квадратов катетов (других двух сторон).
Теорему Пифагора можно записать формулой:
a2 + b2 = c2
Где a и b – длины катетов, а c – длина гипотенузы.
Название теоремы происходит от имени древнегреческого математика Пифагора, который жил в VI-V веках до н.э. Пифагорейская школа изначально изучала тонкие математические соотношения, которые затем были обобщены и сформулированы в виде теоремы Пифагора.
Теорема Пифагора широко применяется в геометрии и физике, а также на практике в строительстве и навигации. Она является одним из основных элементов пирамиды знаний и позволяет решать разнообразные задачи с использованием геометрических преобразований и формул.
Важно помнить, что теорема Пифагора применима только для прямоугольных треугольников, где один из углов равен 90°. Во всех остальных случаях она не справедлива.
Определение теоремы Пифагора

Теорема названа в честь греческого математика Пифагора, который впервые ее доказал в 6 веке до нашей эры. Его открытие имело огромное значение для развития геометрии и математики в целом.
Математическое выражение теоремы Пифагора можно записать следующим образом:
- Для прямоугольного треугольника с катетами a и b и гипотенузой c:
a^2 + b^2 = c^2
Это выражение позволяет решать различные задачи, связанные с прямоугольными треугольниками. Например, зная длины двух сторон, можно найти длину третьей стороны, проверить, является ли треугольник прямоугольным, или найти площадь треугольника.
Теорема Пифагора является одним из основных инструментов геометрии и находит широкое применение не только в математике, но и в физике, инженерии, архитектуре и других областях.
Правила знаков в теореме Пифагора
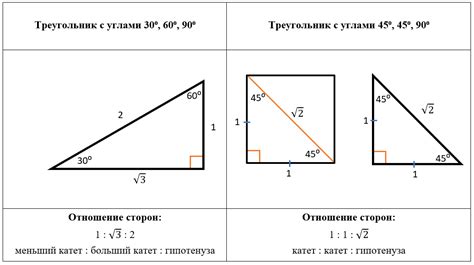
Формулировка теоремы Пифагора звучит следующим образом: "В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов".
Важно заметить, что в теореме Пифагора имеются некоторые правила относительно знаков длин сторон треугольника:
1. Длина стороны не может быть отрицательной: в теореме Пифагора рассматриваются только положительные величины.
2. Знаки длин катетов не имеют значения: в теореме Пифагора используются квадраты длин сторон, поэтому знаки катетов не важны. Результат теоремы будет одинаковым вне зависимости от знаков длин катетов.
3. Знак длины гипотенузы зависит от знаков катетов: если оба катета положительные или оба отрицательные, то гипотенуза также будет положительной. Если один из катетов положительный, а другой отрицательный, то гипотенуза будет отрицательной.
Примечание: В случае использования теоремы Пифагора для нахождения длины сторон треугольника, необходимо учитывать правила знаков для получения корректного результата.
Применение теоремы Пифагора в геометрии
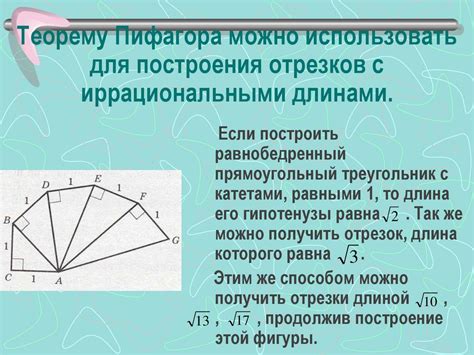
Согласно теореме Пифагора, в прямоугольном треугольнике с гипотенузой c и катетами a и b справедлива следующая формула:
c2 = a2 + b2
Таким образом, можно определить длину гипотенузы или одного из катетов по известным значениям. Кроме того, теорема Пифагора позволяет проверять, является ли треугольник прямоугольным, поскольку она выполняется только для таких треугольников.
Применение теоремы Пифагора не ограничивается только нахождением длин сторон. Её можно использовать и в других геометрических задачах. Например, для нахождения расстояния между двумя точками на плоскости, можно использовать координатный способ, который основан на теореме Пифагора.
Теорема Пифагора является важным инструментом для геометров, инженеров и многих других специалистов. Позволяя находить неизвестные значения и проверять прямоугольность треугольников, она помогает решать задачи практического и научного характера.
Примеры использования теоремы Пифагора

- Вычисление длины гипотенузы треугольника. Если известны длины катетов треугольника, то с помощью теоремы Пифагора можно вычислить длину его гипотенузы. Для этого необходимо возвести в квадрат длины каждого катета, сложить их и извлечь из результата квадратный корень.
- Определение прямоугольности треугольника. Если сумма квадратов длин катетов треугольника равна квадрату длины его гипотенузы, то треугольник является прямоугольным.
- Расчет расстояния между двумя точками на плоскости. Если координаты двух точек на плоскости известны, то с помощью теоремы Пифагора можно вычислить расстояние между этими точками. Для этого необходимо разность координат по каждой оси возвести в квадрат, сложить полученные значения и извлечь из результата квадратный корень.
- Расчет расстояния между двумя точками в пространстве. Аналогично расчету расстояния на плоскости, с помощью теоремы Пифагора можно вычислить расстояние между двумя точками в трехмерном пространстве. Для этого необходимо разность координат по каждой оси возвести в квадрат, сложить полученные значения и извлечь из результата квадратный корень.
- Нахождение высоты треугольника. Если известны длины сторон треугольника, то с помощью теоремы Пифагора можно вычислить длину его высоты, проведенной к основанию. Для этого необходимо квадрат длины высоты выразить через квадраты длин сторон треугольника.
Теорема Пифагора является мощным инструментом для решения различных геометрических задач, а также находит применение в физике, инженерии и других научных областях.