Дерево решений – это один из основных алгоритмов машинного обучения, который может использоваться для классификации и регрессии. Оно представляет собой структуру данных, которая имитирует дерево, где каждый узел представляет собой признак, а каждая ветвь – возможное значение признака. Дерево строится на основе обучающих данных и использования различных алгоритмов, которые помогают принимать решения и делать прогнозы.
Зачем использовать дерево решений?
Дерево решений обладает рядом преимуществ, которые делают его популярным и удобным инструментом для машинного обучения. Во-первых, оно позволяет наглядно представить и объяснить принимаемые решения. Каждый узел выражает логическое условие, которое помогает понять, какие признаки влияют на конечное решение. Во-вторых, дерево решений способно обрабатывать как категориальные, так и числовые данные. А еще, оно устойчиво к выбросам, что позволяет получать более точные результаты в сравнении с другими алгоритмами.
Принцип работы дерева решений
Основная идея дерева решений заключается в разбиении исходного набора данных на подмножества, таким образом, чтобы в каждом подмножестве находились объекты, которые имеют схожие значения целевой переменной или принадлежат одному классу. Процесс разбиения основан на использовании различных метрик, таких как энтропия и неопределенность Джини. Цель – минимизировать энтропию и неопределенность, чтобы получить наиболее точное дерево решений.
Определение дерева решений в машинном обучении
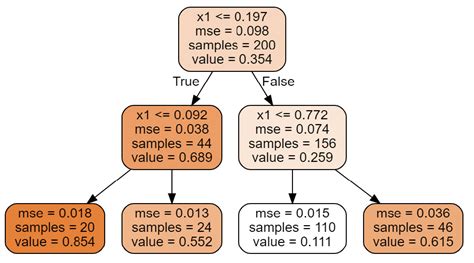
Дерева решений являются одним из наиболее популярных и простых алгоритмов машинного обучения. Построение дерева решений происходит на основе обучающих примеров, где каждый пример представляет собой набор признаков и соответствующий класс или результат. Алгоритм стремится определить признаки, которые наилучшим образом разделяют данные на отдельные классы или категории.
Процесс построения дерева решений начинается с корневого узла, который соответствует всем данным. Затем алгоритм выбирает наилучший признак для разделения данных. Этот процесс повторяется для каждого созданного поддерева, пока не достигнут критерий остановки, такой как достижение определенной глубины дерева или недостаточное количество примеров в узле.
После построения дерева решений оно может быть использовано для принятия решений для новых данных. Алгоритм проходит по ветвям дерева, на основе значений признаков, и достигает листа, который соответствует классу или решению для конкретного набора данных.
Деревья решений имеют много преимуществ, включая простоту интерпретации и понимания полученных результатов, способность работать с различными типами данных и хорошую масштабируемость для больших объемов данных. Однако, они также могут быть склонны к переобучению и не учитывать сложные взаимодействия между признаками данных.
Принцип работы дерева решений
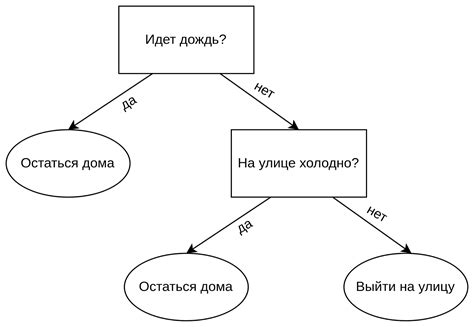
Основной принцип работы дерева решений заключается в разделении данных на группы на основе значимых атрибутов, которые позволяют классифицировать данные. Дерево строится пошагово, начиная с корневого узла и последовательно спускаясь по ветвям до листьев, где принимается окончательное решение.
Каждое разделение данных осуществляется на основе определенного атрибута и его значения. Алгоритм строит дерево таким образом, чтобы наиболее информативные атрибуты находились ближе к корню, а наименее информативные - ближе к листьям. Критерий выбора оптимального разделения может зависеть от конкретной задачи и используемого алгоритма.
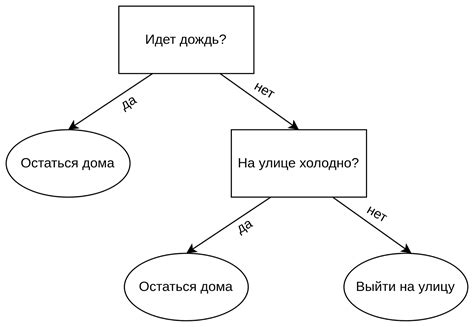
Пример работы дерева решений:
Допустим, мы хотим классифицировать фрукты на основе их цвета, формы и текстуры. Первое разделение может быть сделано на основе цвета фрукта: например, разделить на красные и не красные фрукты. Затем, для каждой из этих групп можно провести новое разделение, например, на основе формы фрукта. Продолжая этот процесс, мы будем описывать все более специфические атрибуты, пока не достигнем итоговых результатов.
В результате работы дерева решений мы получаем графическое представление процесса классификации данных. Каждый лист дерева представляет конечное решение, которое алгоритм принимает на основе заданных условий.
Преимущества использования дерева решений
- Простота понимания и интерпретации: Дерево решений представляет собой иерархическую структуру решений, которая легко понятна и интерпретируема даже неспециалистам. Визуализация дерева позволяет легко увидеть логическую цепочку принятия решений и понять, какие переменные и условия влияют на итоговый результат.
- Универсальность применения: Дерево решений может быть использовано для решения широкого спектра задач, включая классификацию, регрессию и кластеризацию данных. Это делает его универсальным инструментом для анализа данных и прогнозирования.
- Обработка разнотипных данных: Дерево решений может работать с разнотипными данными, включая категориальные, числовые и бинарные переменные. Оно автоматически выбирает оптимальное разделение для каждого типа переменной, что позволяет извлечь максимум информации и улучшить точность прогнозирования.
- Высокая скорость обучения и прогнозирования: Дерево решений имеет высокую скорость обучения и прогнозирования, особенно на небольших и средних объемах данных. Алгоритм эффективно разбивает пространство признаков на подмножества и решает каждую часть независимо, что позволяет сократить количество вычислений и ускорить процесс.
- Работа с пропущенными значениями и выбросами: Дерево решений может эффективно обрабатывать пропущенные значения и выбросы в данных. Оно может автоматически заполнять пропущенные значения и учитывать выбросы в процессе разбиения и прогнозирования, что позволяет получить более точные результаты.
В целом, дерево решений представляет собой мощный инструмент для анализа данных и прогнозирования. Его простота, интерпретируемость и универсальность делают его особенно полезным для начинающих исследователей и аналитиков данных.
Ограничения и недостатки дерева решений
Переобучение: Деревья решений могут быть склонны к переобучению, особенно если у них есть большое количество уровней или узлов. Это означает, что модель может "запомнить" конкретные примеры в обучающем наборе данных и не сможет обобщить полученные знания на новые данные.
Чувствительность к данным: Деревья решений могут быть чувствительны к небольшим изменениям в данных, что может привести к существенным изменениям в построенном дереве. Это может сделать модель нестабильной и менее надежной.
Трудность нахождения оптимального дерева: Поиск оптимального дерева решений может быть вычислительно сложной задачей, особенно когда имеется большое количество признаков или узлов. Это требует значительного объема вычислительных ресурсов и времени.
Неэффективность на больших данных: Деревья решений могут быть неэффективными на больших наборах данных, так как алгоритму может потребоваться обработать большое количество данных, чтобы принять решение, что может быть трудоемким и медленным процессом.
Проблема мультиколлинеарности: Если в данных присутствуют признаки, которые сильно коррелируют друг с другом (мультиколлинеарность), деревья решений могут иметь проблему выбора наиболее важного признака для разделения узлов, что может привести к менее точным результатам.
Отсутствие интерпретируемости: В отличие от некоторых других моделей машинного обучения, деревья решений не всегда легко интерпретируются. Они представляют собой сложные структуры с множеством узлов и ветвей, что может затруднить понимание причинно-следственных связей в данных.
Несмотря на эти ограничения и недостатки, деревья решений остаются одним из наиболее популярных методов машинного обучения благодаря своей простоте и способности принимать решения на основе логических правил.
Ограничения дерева решений
1. Недостаток обобщающей способности: Дерево решений может быть склонно к переобучению, особенно когда данные слишком сложные или шумные. Это может привести к плохой обобщающей способности модели и низкому качеству предсказаний на новых данных.
2. Чувствительность к изменениям в данных: Дерево решений может быть чувствительным к незначительным изменениям в обучающих данных. Даже небольшое изменение в данных может привести к совершенно различным результатам, что делает его нестабильным.
3. Проблема мультиколлинеарности: Если в обучающих данных есть переменные, которые сильно коррелируют между собой, дерево решений может столкнуться с проблемой мультиколлинеарности. Это может привести к неправильным или неинтерпретируемым результатам.
4. Трудность в обработке числовых данных: Дерево решений обычно лучше работает с категориальными данными, чем с числовыми. Обработка числовых данных может потребовать дополнительной предобработки, такой как дискретизация или биниризация.
5. Необходимость выбора оптимальных параметров: Дерево решений имеет некоторые параметры, такие как глубина дерева или критерии разделения, которые могут влиять на его производительность. Правильный выбор этих параметров может быть нетривиальной задачей и потребовать экспериментов.
Не смотря на эти ограничения, дерево решений всё же является популярным алгоритмом машинного обучения благодаря своей простоте, интерпретируемости и способности решать различные задачи.
Если вы правильно учитываете ограничения дерева решений и правильно применяете его в конкретной задаче, то он может быть мощным инструментом для получения ценных и интерпретируемых результатов.
Недостатки дерева решений
- Переобучение: Деревья решений могут быть склонны к переобучению, особенно если количество признаков велико и дерево становится сложным. В результате получается модель, которая хорошо объясняет тренировочные данные, но плохо обобщает на новые данные. Недооценка и оптимизация глубины дерева помогают бороться с этой проблемой.
- Чувствительность к данным: Деревья решений могут быть чувствительны к малейшим изменениям в данных. Даже небольшое изменение в тренировочных данных может привести к значительным изменениям в структуре и поведении дерева решений. Это может быть проблематично при работе с шумными данными или данными с выбросами.
- Неподходящие данные: Деревья решений имеют тенденцию неэффективно работать с некоторыми типами данных. Например, они не работают хорошо с категориальными данными, поскольку деревья решений строятся на основе порогового значения признака. В таких случаях необходимо применять методы преобразования данных, чтобы сделать их подходящими для деревьев решений.
- Долгое время обучения: Построение сложного дерева решений может занять много времени, особенно если данные имеют большой размер. Решением этой проблемы может быть использование алгоритмов, которые работают быстрее, например, случайный лес.
Несмотря на эти недостатки, деревья решений остаются полезным инструментом в машинном обучении и широко применяются в различных областях, благодаря своей способности к интерпретации результатов и простоте в использовании.
Как построить и обучить дерево решений
Вот шаги, которые необходимо выполнить для построения и обучения дерева решений:
| Шаг | Описание |
| 1 | Собрать данные |
| 2 | Выбрать атрибуты |
| 3 | Построить дерево |
| 4 | Обучить дерево |
Первым шагом является сбор данных. Для обучения дерева необходимо иметь набор данных, который содержит информацию о классификации или предсказании. Набор данных должен быть достаточно разнообразным и репрезентативным для общей ситуации.
На следующем шаге необходимо выбрать атрибуты, которые будут использоваться для построения дерева решений. Атрибуты должны быть информативными и хорошо отражать свойства классифицируемого объекта или предсказываемой переменной.
Построение дерева - это процесс разбиения данных на подмножества на основе выбранных атрибутов. Разбиение выполняется на основе определенного критерия, как, например, индекс Джини или энтропия. Цель состоит в том, чтобы максимально уменьшить неопределенность в каждом подмножестве данных.
Наконец, дерево обучается на основе данных и выбранного критерия разбиения. Обучение дерева заключается в настройке параметров и выборе оптимальных значений для максимизации точности классификации или предсказания. Этот шаг может включать шаги, такие как обработка пропущенных данных, масштабирование атрибутов и настройка параметров алгоритма.
Теперь вы знаете, как построить и обучить дерево решений. Этот алгоритм может быть мощным инструментом в вашей корзине машинного обучения, поэтому не стесняйтесь применять его для различных задач классификации или регрессии.
Шаги построения дерева решений
Построение дерева решений в машинном обучении включает ряд важных шагов. Начнем с основного алгоритма, который позволяет построить дерево решений.
Шаг 1: Загрузка данных
Первым шагом является загрузка данных, на которых будет тренироваться дерево решений. Это могут быть данные, представленные в виде таблицы или файлов.
Шаг 2: Подготовка данных
После загрузки данных необходимо провести анализ и предварительную обработку. Это включает в себя проверку на наличие отсутствующих значений, выбросов, а также преобразование категориальных данных в числовой формат.
Шаг 3: Разделение на обучающую и тестовую выборки
Для оценки качества модели необходимо разделить общий набор данных на две части: обучающую выборку и тестовую выборку. Обучающая выборка будет использоваться для обучения модели, а тестовая выборка - для оценки ее предсказательной способности.
Шаг 4: Обучение модели
На этом шаге происходит обучение дерева решений с использованием обучающей выборки. Алгоритм строит дерево, учитывая разделение данных на основе признаков и критериев ветвления.
Шаг 5: Оценка модели
После обучения модели необходимо произвести оценку ее качества на тестовой выборке. Это может быть выполнено с помощью различных метрик, таких как точность, полнота, F-мера и др.
Шаг 6: Тонкая настройка модели
После оценки модели возможно ее дальнейшее улучшение. Это может включать в себя изменение гиперпараметров модели, таких как глубина дерева, критерии разделения и т.д.
Шаг 7: Применение модели
После завершения всех предыдущих шагов модель готова к использованию. Она может быть применена для предсказания значений на новых данных или решения задач классификации и регрессии.
Именно таким образом можно построить дерево решений в машинном обучении и использовать его для решения разнообразных задач. Знание этих шагов поможет вам стать более компетентным и уверенным специалистом в области машинного обучения.
Обучение дерева решений
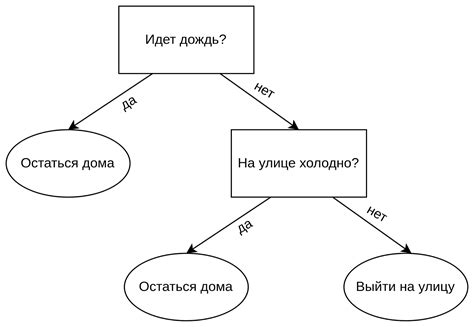
Обучение дерева решений начинается с выбора корневого узла, который характеризуется наибольшей энтропией или информационной неопределенностью. Затем происходит разделение данных на две или более ветви, используя определенный признак или характеристику.
Процесс разделения данных продолжается, пока все объекты не будут отнесены к одному классу или пока не будет достигнут критерий остановки. Критерии остановки могут быть различными, включая достижение определенной глубины дерева, достижение определенного количества объектов в узле или достижение достаточного уровня информационного прироста.
Обучение дерева решений также включает расчет весовых коэффициентов для каждого признака, которые определяют важность каждого признака в принятии решения. Эти коэффициенты используются в процессе разделения данных и определения значимости каждого признака.
После завершения обучения дерева решений, модель становится способной принимать решения на основе заданных признаков или характеристик. Она может быть использована для классификации объектов или предсказания значений целевой переменной.
| Преимущества обучения дерева решений: | Недостатки обучения дерева решений: |
|---|---|
| - Простота интерпретации - Может работать с категориальными и числовыми данными - Способность работать с отсутствующими данными | - Неустойчивость к изменению данных - Возможность переобучения - Трудность в обработке больших данных |
Одним из методов улучшения работы дерева решений является ансамбльное обучение, такое как случайный лес или градиентный бустинг. При использовании ансамбля моделей, можно достичь более точных результатов и улучшить обобщающую способность дерева решений.