Ромб - это геометрическая фигура, которая относится к классу параллелограммов. Однако, в отличие от обычных параллелограммов, ромб обладает некоторыми особенностями, которые делают его уникальным и интересным объектом изучения.
Одной из главных особенностей ромба является его форма. За счет равенства всех сторон, ромб обладает высокой симметрией, что делает его привлекательным для использования в дизайне и архитектуре. Неповторимый эстетический вид ромба привлекает внимание и вызывает интерес у людей.
Вторая особенность ромба заключается в его свойствах. Ромб обладает свойством растворимости, то есть его стороны легко разделяются на две половины параллелей. Это свойство позволяет выполнять некоторые геометрические преобразования и расчеты с ромбом.
Существует несколько способов определения ромба. Один из них - определение по сторонам. Если все стороны ромба равны между собой, то это основание для утверждения, что фигура является ромбом. Также можно определить ромб по диагоналям - если они перпендикулярны и равны, то фигура также является ромбом.
Особенности ромба
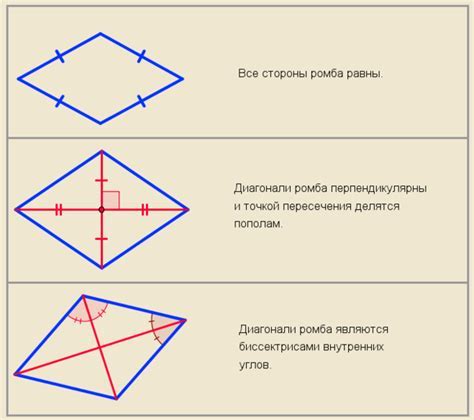
У ромба также есть несколько характеристических особенностей:
| 1. Углы | Все углы ромба равны между собой. Каждый угол ромба составляет по 90 градусов. |
| 2. Диагонали | Диагонали ромба являются его основными элементами. Они являются взаимно перпендикулярными и делят ромб на четыре равных треугольника. |
| 3. Площадь и периметр | Площадь ромба можно вычислить, зная длину одной из его сторон или длины диагоналей. Периметр ромба можно найти, умножив длину одной стороны ромба на 4. |
| 4. Равнобедренность | Ромб является равнобедренным четырехугольником, у которого все четыре боковые стороны равны. В результате, высоты ромба под сторонами равны друг другу. |
Все эти особенности делают ромб уникальной и интересной геометрической фигурой, которая имеет множество применений в различных областях.
Форма и конструкция

1. Все стороны ромба равны между собой. Это означает, что сторона AB равна стороне BC, а также стороне CD и стороне DA.
2. Углы ромба также имеют равные величины. Это означает, что угол ABC равен углу BCD, а также углам CDA и DAB.
3. Диагонали ромба являются взаимно перпендикулярными. Это значит, что диагонали AC и BD пересекаются под прямым углом.
4. Диагонали ромба делятся пополам. Это значит, что точка пересечения диагоналей является центром симметрии ромба и разделяет его на четыре равных треугольника.
5. Все углы ромба равны 90 градусов. Это прямоугольный ромб, который также является квадратом.
Такие особенности формы и конструкции ромба делают его удобным для решения различных задач, связанных с геометрией и строительством. Он является симметричной фигурой с равными сторонами и углами, что позволяет использовать его в качестве базовой формы для создания различных объектов и конструкций.
Стороны и углы
- Все четыре стороны ромба равны между собой.
- Противоположные стороны ромба параллельны друг другу.
- Углы ромба имеют следующие характеристики:
1. Все углы ромба равны между собой.
2. Сумма всех углов ромба составляет 360 градусов.
3. Каждый угол ромба равен 90 градусам.
Благодаря этим особенностям сторон и углов ромба, он является фигурой симметричной формы и идеально подходит для различных приложений в геометрии, строительстве и дизайне.
Ромб как параллелограмм
Основная особенность ромба заключается в том, что все его стороны являются равными между собой. Это означает, что любой ромб может быть описан окружностью, касающейся всех его вершин. Кроме того, ромб является фигурой с симметрией по отношению к своей диагонали, что делает его особенно привлекательным в геометрических конструкциях и дизайне.
Также, как и любой параллелограмм, ромб обладает свойством противоположных сторон: две пары противоположных сторон параллельны и равны между собой. Кроме того, ромб также обладает свойством противоположных углов: две пары противоположных углов равны между собой.
Определить, является ли данная фигура ромбом, можно по нескольким признакам. Во-первых, стороны ромба должны быть равны между собой. Во-вторых, диагонали ромба должны перпендикулярны друг другу и делиться внутри ромба пополам.
Как определить ромб:
- Измерьте все стороны фигуры и проверьте их равенство.
- Измерьте диагонали фигуры и проверьте их перпендикулярность и равность.
- Убедитесь, что фигура удовлетворяет всем указанным свойствам ромба.
Если все эти условия выполнены, то можно с уверенностью утверждать, что данный параллелограмм является ромбом.
Определение параллелограмма
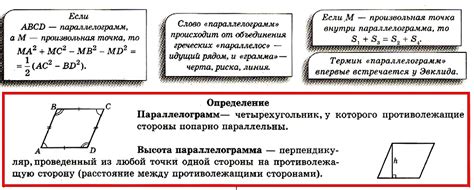
Существует несколько способов определения параллелограмма:
| Способ 1: | Если противоположные стороны параллелограмма одновременно равны и параллельны, то фигура является параллелограммом. |
| Способ 2: | Если противоположные стороны параллелограмма равны по длине и параллельны, а углы между ними равны, то фигура является параллелограммом. |
| Способ 3: | Если противоположные стороны параллелограмма равны по длине и параллельны, а диагонали взаимно делятся пополам, то фигура является параллелограммом. |
С использованием данных определений их можно проверять наличие параллелограмма в геометрических фигурах и устанавливать их свойства.
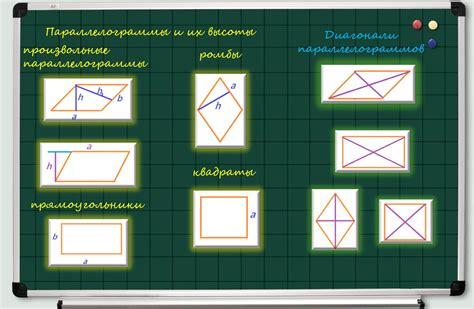
Сравнение с другими параллелограммами

Ромб, как и другие параллелограммы, имеет определенные особенности, которые отличают его от остальных фигур этого типа. Ниже приведена таблица, сравнивающая ромб с такими параллелограммами, как прямоугольник и квадрат:
| Параметр | Ромб | Прямоугольник | Квадрат |
|---|---|---|---|
| Стороны | Все стороны равны | Противоположные стороны равны | Все стороны равны |
| Углы | Все углы равны | Противоположные углы равны | Все углы прямые |
| Диагонали | Диагонали пересекаются в прямом угле | Диагонали равны | Диагонали равны и перпендикулярны |
| Периметр | Сумма всех сторон | Удвоенная сумма противоположных сторон | Удвоенная сумма всех сторон |
| Площадь | Произведение длин диагоналей, деленное на 2 | Произведение длин противоположных сторон | Квадрат одной из сторон |
Таким образом, ромб имеет свои уникальные характеристики, которые делают его особенным среди других параллелограммов. При изучении и использовании ромбов в геометрии и пространственном моделировании необходимо учитывать эти различия.