Правильная четырехугольная пирамида – одна из фигур, обладающих поразительными свойствами и гармоничной структурой. Ее грани, взаимно пересекающиеся, образуют множество параллельных плоскостей. В этой статье мы рассмотрим особенности и свойства параллельных граней правильной четырехугольной пирамиды, и обсудим, как они влияют на ее геометрические параметры и структуру в целом.
Параллельные грани правильной четырехугольной пирамиды – это грани, которые лежат в одной плоскости и никак не пересекаются между собой. Таким образом, при рассмотрении пирамиды с разных сторон, можно увидеть, что ее грани имеют одинаковую форму и ориентацию. Это является одним из ключевых свойств такой пирамиды, которое позволяет ей обладать некоторыми уникальными характеристиками и визуальным воздействием.
Параллельные грани правильной четырехугольной пирамиды создают пространство, которое можно легко разделить на несколько частей, каждая из которых является плоскостью, параллельной другим граням. Это позволяет ученным и математикам исследовать и анализировать различные характеристики пирамиды, такие как объем, площадь поверхности и другие параметры.
Основные свойства правильной четырехугольной пирамиды
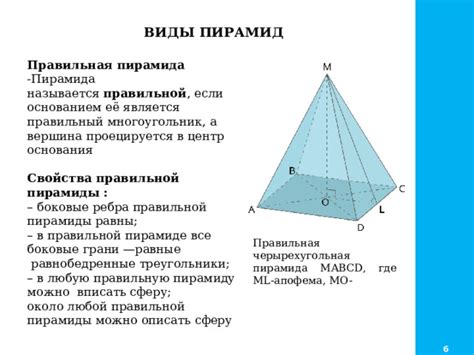
1. Равные грани: В правильной четырехугольной пирамиде все грани равны друг другу. Это означает, что площади и формы всех граней пирамиды одинаковы.
2. Равные углы: Все углы между гранями такой пирамиды равны между собой. Таким образом, значения углов пирамиды будут одинаковыми.
3. Параллельные грани: У правильной четырехугольной пирамиды все грани параллельны основанию пирамиды. Это означает, что каждая грань будет располагаться параллельно другой грани.
4. Равнобедренные треугольники: В правильной четырехугольной пирамиде четыре треугольника, образованные основанием пирамиды и ее ребрами, являются равнобедренными. Это означает, что у них две стороны и два угла равны между собой.
5. Высота и объем: Высота правильной четырехугольной пирамиды - это линия, перпендикулярная плоскости основания и проходящая через вершину пирамиды. Объем такой пирамиды вычисляется по формуле: V = (1/3) * S * h, где S - площадь основания, а h - высота.
6. Площадь поверхности: Площадь поверхности правильной четырехугольной пирамиды вычисляется по формуле: S = Sосн + Sбок, где Sосн - площадь основания, Sбок - сумма площадей боковых граней.
7. Симметрия: У правильной четырехугольной пирамиды существует ось симметрии, проходящая через вершину пирамиды и центр основания. Это означает, что пирамида может быть разделена на две симметричные части.
Правильная четырехугольная пирамида обладает множеством интересных особенностей, которые делают ее уникальной и важной в математике и геометрии.
Геометрическая форма и структура
Пирамида имеет центральную ось, проходящую через вершину, а также две параллельные плоскости, проходящие через основание и через среднюю точку каждой боковой грани. Таким образом, грани пирамиды являются параллельными парами: основание и верхняя грань параллельны друг другу, а боковые грани пирамиды также параллельны между собой.
Эта особенность структуры пирамиды позволяет ей обладать рядом интересных свойств. Например, параллельность граней обеспечивает симметрию пирамиды относительно центральной оси. Каждая боковая грань является подобной и равнобедренной, а угол между плоскостью основания и боковой гранью равен 60 градусам.
Кроме того, параллельные грани пирамиды определяют ее объем. Для правильной четырехугольной пирамиды, объем вычисляется по формуле: V = (a^2 * h)/3, где a - длина стороны основания, h - высота пирамиды.
Таким образом, геометрическая форма и структура правильной четырехугольной пирамиды обладают уникальными свойствами, связанными с расположением и связью параллельных граней. Эти особенности являются основой для дальнейшего изучения и применения пирамиды в различных математических и научных областях.
Число граней, ребер и вершин
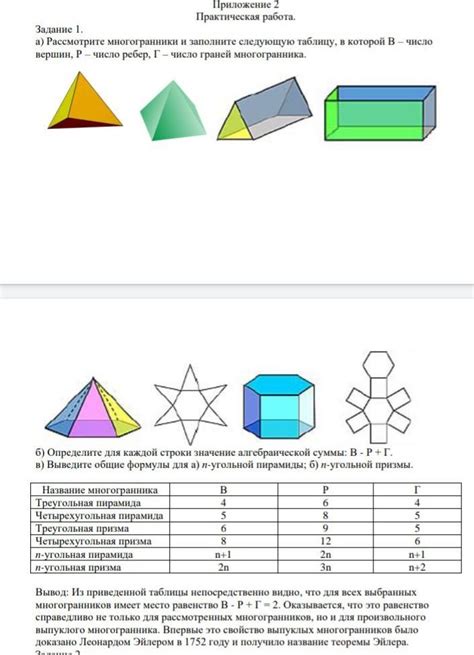
Количество ребер в правильной четырехугольной пирамиде составляет 8. Каждая вершина пирамиды соединена с тремя ребрами, а вершин всего четыре.
Число вершин в правильной четырехугольной пирамиде равно 5. Четыре вершины находятся в пересечении боковых граней пирамиды, а пятая вершина находится на основании пирамиды.
Уникальные особенности фигуры

Параллельные грани правильной четырехугольной пирамиды обладают рядом уникальных свойств и особенностей.
1. Равнобедренность основания: каждая из параллельных граней пирамиды прилегает к основанию, которое является равнобедренной трапецией. Это означает, что длины двух противоположных сторон основания равны.
2. Плоскостные фигуры: грани пирамиды являются плоскостными фигурами, что значительно упрощает его геометрические вычисления и анализ. Это также позволяет визуализировать и понять структуру пирамиды с помощью двухмерных моделей.
3. Центральная симметрия: каждая параллельная грань пирамиды лежит в плоскости, проходящей через центр пирамиды. Это означает, что фигура обладает центральной симметрией - ее можно разделить на две одинаковые части с помощью плоскости, проходящей через ее центр.
4. Устойчивость конструкции: благодаря параллельным граням, правильная четырехугольная пирамида обладает высокой устойчивостью. Это позволяет использовать ее в строительстве и других инженерных проектах, где требуется прочная и надежная конструкция.
5. Уникальная форма: смешение плоских и объемных форм делает пирамиду уникальной и характерной фигурой. Ее простая, но элегантная форма впечатляет и привлекает внимание, делая пирамиду одной из самых узнаваемых и уникальных геометрических фигур.
Все эти особенности делают параллельные грани правильной четырехугольной пирамиды интересным объектом изучения и применения в различных областях науки, техники и искусства.
Способы построения правильной четырехугольной пирамиды
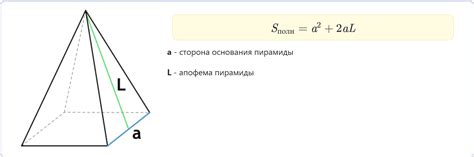
Существует несколько способов построения правильной четырехугольной пирамиды:
1. С использованием высоты и бокового ребра Данный способ основывается на построении высоты и бокового ребра пирамиды. Сначала можно построить основание пирамиды, являющееся равнобедренным треугольником. Затем, используя высоту и боковое ребро, можно построить оставшиеся грани пирамиды. | 2. С использованием высоты и плоскостей проекций Для этого способа необходимо построить основание и высоту пирамиды, а затем определить плоскости проекций для каждой грани пирамиды. Таким образом, можно построить все грани пирамиды, используя плоскости проекций и основание. |
3. С использованием основания и направляющих линий Этот способ заключается в построении основания пирамиды, а затем задании направляющих линий, которые помогут построить боковые грани пирамиды. Направляющие линии соединяют вершины основания с вершиной пирамиды, образуя равнобедренные треугольники. | 4. С использованием бокового ребра и плоскости проекции Для этого способа необходимо задать боковое ребро и определить плоскость проекции. Затем можно построить основание пирамиды и использовать плоскость проекции для построения боковых граней пирамиды. |
Каждый из этих способов имеет свои особенности и может быть использован в разных ситуациях. Выбор способа зависит от доступных данных и конкретных требований к пирамиде.
Необходимо учитывать, что правильная четырехугольная пирамида имеет ряд свойств, таких как равенство углов, равенство боковых ребер и диагоналей основания и другие. Изучение данных свойств позволяет более полно представить форму и структуру пирамиды.
Параллельные грани пирамиды: определение и свойства
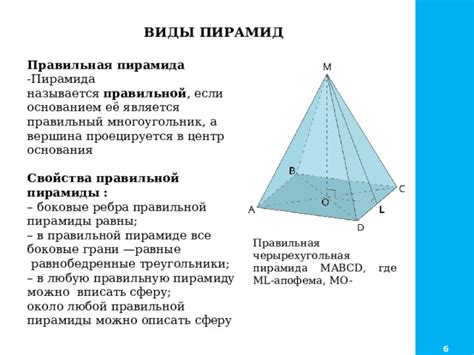
Свойства параллельных граней пирамиды:
- Параллельность: Грани пирамиды, расположенные на разных уровнях, лежат в параллельных плоскостях. Это означает, что если одну из граней продолжить в направлении, параллельном плоскости пирамиды, она пересечет другие грани на одинаковом расстоянии.
- Соотношения: Параллельные грани пирамиды имеют определенные соотношения между сторонами и углами. Например, в правильной четырехугольной пирамиде боковые грани являются равнобедренными треугольниками, а боковые ребра равны между собой.
- Основание и вершина: Параллельные грани пирамиды образуют ее основание и вершину. Основание представляет собой плоскость, на которой лежат боковые грани пирамиды. Вершина пирамиды находится на прямой, перпендикулярной плоскости основания и проходящей через центр основания.
Изучение параллельных граней позволяет более глубоко понять структуру и свойства пирамиды. Они служат основой для определения ее объема, площади поверхности и угловых свойств. Параллельные грани являются ключевым элементом в анализе и конструировании пирамиды, а их свойства важны для различных прикладных задач.
Значение параллельных граней в архитектуре

Параллельные грани правильной четырехугольной пирамиды играют важную роль в архитектуре. Они позволяют создавать уникальные и запоминающиеся формы зданий. Параллельные грани могут быть использованы для создания сложных объемов и визуальных эффектов, которые привлекают внимание и создают интересные комбинации в архитектуре.
Одно из значимых свойств параллельных граней – возможность создания впечатляющих фасадов. Благодаря их параллельным сторонам, архитекторы могут играть с геометрическими формами и создавать гармоничные проекции. При этом параллельные грани придают зданию солидности и структурности, делая его более визуально привлекательным.
Также, параллельные грани могут служить в качестве опорных элементов для других дизайнерских решений. Они могут стать основой для создания фасадных окон или дверных проемов, а также использоваться как полосы декоративных элементов, таких как ленты или фризы. Эти элементы придают зданию уникальность и характер, делая его узнаваемым и запоминающимся.
Еще одним важным свойством параллельных граней является их способность создавать объемные эффекты. Использование параллельных форм позволяет архитекторам создавать динамичные формы здания и играть с перспективой. Это помогает добавить интерес и эстетическую привлекательность в архитектурный облик здания.
В заключении, можно сказать, что параллельные грани правильной четырехугольной пирамиды – это один из ключевых элементов в архитектуре, способный добавить впечатляющий и характерный вид зданию. Их использование позволяет архитекторам реализовывать свою креативность и создавать уникальные и запоминающиеся проекты.
Практическое применение параллельных граней
Правильные четырехугольные пирамиды с параллельными гранями имеют множество практических применений в различных областях. Вот некоторые из них:
1. Архитектура и строительство: Параллельные грани пирамиды могут использоваться для создания прочных и устойчивых конструкций. Они обеспечивают равномерное распределение нагрузки и повышают стабильность зданий и мостов.
2. Геометрическое моделирование: Параллельные грани пирамиды могут использоваться в компьютерной графике и 3D-моделировании для создания различных форм и структур. Они позволяют точно воспроизвести сложные геометрические объекты.
3. Физика и инженерия: Параллельные грани пирамиды могут служить моделями для исследования физических законов и основных принципов механики. Они помогают понять взаимодействие тел и сил, а также разрабатывать новые технологии и материалы.
4. Математика и образование: Параллельные грани пирамиды позволяют учить и практиковать геометрию, а также развивать способности к абстрактному мышлению. Они используются в учебных пособиях и задачах для обучения школьников и студентов основам геометрии и пространственного мышления.
5. Интерьерный дизайн: Пирамиды с параллельными гранями могут использоваться для создания оригинальных и красивых предметов интерьера, таких как светильники, вазы, наборы для хранения и декоративные элементы. Они придают пространству уникальный вид и эстетическое значение.
Параллельные грани правильной четырехугольной пирамиды представляют собой важный элемент в различных областях человеческой деятельности. Их свойства и особенности позволяют применять их с пользой и эффективностью в разнообразных задачах и проектах.