Понимание параллельности прямых ab и cd является одним из основных элементов геометрии. Данная статья представляет собой обзор основных условий, доказательств и примеров параллельных прямых.
Условием параллельности прямых ab и cd является их отношение: они должны быть одновременно перпендикулярны к одной и той же прямой. Иначе говоря, если прямые ab и cd пересекаются, то они не являются параллельными.
Доказательство параллельности прямых ab и cd может быть выполнено различными способами, в зависимости от заданных условий и требуемой точности доказательства. Одним из наиболее распространенных методов является использование аксиом и определений геометрии, таких как аксиома параллельных прямых Евклида и определение параллельности. Используется также метод сравнения углов, сравнения расстояний между точками прямых, а также метод подобия и соотношения пропорциональности.
Приведены также примеры параллельных прямых, вычисленных на основе полученных условий и доказательств. Данные примеры помогут лучше понять принципы параллельности прямых, а также применение этих принципов в решении задач, связанных с геометрией и анализом прямых.
Условия параллельности прямых ab и cd

- Условие 1: Углы между прямыми равны. Если угол между прямыми ab и cd равен углу между прямыми ef и gh, то можно заключить, что прямые ab и cd параллельны.
- Условие 2: Прямые имеют одинаковый угловой коэффициент. Если прямая ab имеет угловой коэффициент k1, а прямая cd имеет угловой коэффициент k2, и эти коэффициенты равны, то прямые ab и cd параллельны.
- Условие 4: Прямые имеют общую нормальную прямую. Если две прямые ab и cd имеют общую нормальную прямую ef, то они параллельны.
Важно помнить, что существует много различных способов проверить параллельность прямых. Использование одного условия может быть недостаточно для достоверного утверждения о параллельности, поэтому рекомендуется проверять несколько условий одновременно.
Соотношение углов
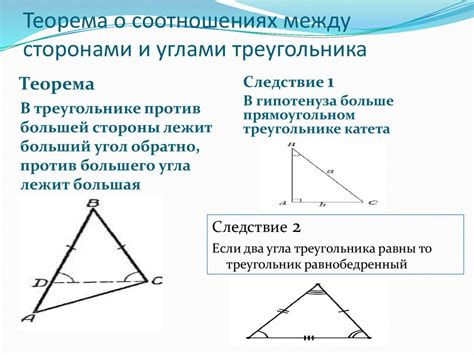
При рассмотрении параллельных прямых ab и cd возникает необходимость определить, как связаны между собой углы, образованные этими прямыми и другими линиями.
Одним из ключевых соотношений, связанных с параллельными прямыми, является так называемое "взаимное соотношение" углов.
Если две параллельные прямые ab и cd пересекаются третьей прямой ef, то углы, образованные параллельными прямыми ab и cd с третьей прямой ef, будут иметь следующее соотношение:
1. Углы, лежащие на одной и той же стороне прямых: если у нас есть два угла, один образованный параллельными прямыми ab и cd и третьей прямой ef, а другой образованный параллельными прямыми cd и ef и третьей прямой ab, то эти углы будут равными (как правило, это называют "корреспондирующими" или "соответственными" углами).
2. Углы, лежащие по разные стороны от прямых: если у нас есть два угла, один образованный параллельными прямыми ab и cd и третьей прямой ef, а другой образованный параллельными прямыми ef и cd и третьей прямой ab, то сумма этих углов будет равна 180 градусам (как правило, это называют "смежными" или "вертикальными" углами).
Соотношение углов является важным инструментом для доказательства различных геометрических теорем, а также для решения задач на построение и вычисление размеров углов.
Соответствующие углы

Для доказательства равенства соответствующих углов можно использовать различные методы. Например, можно использовать факт, что если две параллельные прямые пересекаются с третьей прямой, то сумма соответствующих углов равна 180°.
Пример:
Дано: Прямая ab параллельна прямой cd, прямая ef пересекает обе параллельные прямые.
Найти: Меру угла 1.
Решение:
Мы знаем, что углы 1 и 2 являются соответствующими углами, так как они находятся между параллельными прямыми и имеют одинаковую меру. Кроме того, известно, что угол 2 равен 40°.
Таким образом, мера угла 1 равна 40°.
Прямые, пересекающиеся с параллельными прямыми
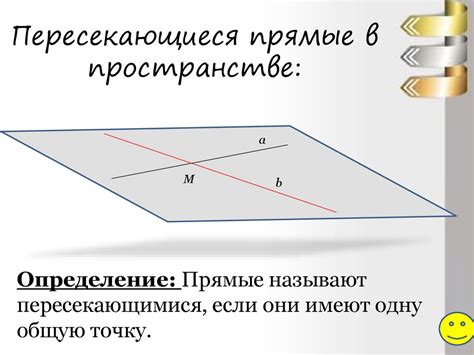
Параллельные прямые ab и cd обладают некоторыми интересными свойствами, когда речь идет о других прямых, пересекающих их. Рассмотрим некоторые ключевые моменты и условия:
- Перпендикулярные прямые: Если прямая ef перпендикулярна параллельным прямым ab и cd, то она будет перпендикулярна их плоскости. Это свойство очень полезно при решении задач на нахождение площадей фигур, ограниченных параллельными прямыми и перпендикулярной к ним прямой.
- Углы их плоскостей: Если прямая ef пересекает параллельные прямые ab и cd, то углы, образованные этой прямой с прямыми ab и cd, будут равны. Это свойство является следствием соответственных углов, образованных параллельными прямыми и пересекающей их трансверсальной прямой.
- Соответствующие углы: Если прямая ef пересекает параллельные прямые ab и cd, то соответствующие углы, образованные этой прямой с прямыми ab и cd, будут равны. Это свойство также помогает в решении задач на нахождение углов.
Прямые, пересекающиеся с параллельными прямыми, играют важную роль в геометрии и находят применение в различных областях. Понимание и использование этих свойств позволяет решать разнообразные задачи с легкостью и точностью.
Доказательства параллельности прямых ab и cd

Ниже представлены некоторые основные методы доказательства параллельности прямых:
- Угловое доказательство. Если углы, образованные прямыми ab и cd и пересекающей их прямой, равны, то прямые ab и cd параллельны.
- Теорема о соответственных углах. Если две прямые ab и cd пересекаются с третьей прямой ef так, что соответственные углы равны, то прямые ab и cd параллельны.
- Использование свойств треугольников. Если треугольники, образованные прямыми ab и cd и третьей прямой ef, подобны друг другу, то прямые ab и cd параллельны.
- Использование свойств прямых углов. Если углы, образованные прямой ab и пересекающей ее прямой, являются прямыми углами, то прямые ab и cd параллельны.
Это лишь некоторые из возможных доказательств параллельности прямых ab и cd. В каждом конкретном случае необходимо анализировать доступные условия и выбирать наиболее подходящий метод доказательства. Знание и применение этих методов помогут в решении задач геометрии, связанных с параллельными прямыми ab и cd.
Доказательство с применением алгебры

Доказательство параллельности прямых ab и cd можно осуществить с помощью алгебраических выражений и свойств прямых. Рассмотрим следующий пример:
- Предположим, что уравнения прямых ab и cd заданы в виде y = mx + b1 и y = mx + b2 соответственно, где m - угловой коэффициент, а b1 и b2 - свободные члены.
- Если прямые ab и cd параллельны, то их угловые коэффициенты должны быть равны, то есть m1 = m2.
- Если уравнения прямых совпадают, то они также параллельны, так как имеют одинаковые угловые коэффициенты и свободные члены.
- Следовательно, чтобы доказать параллельность прямых ab и cd, необходимо и достаточно сравнить их уравнения и убедиться, что они либо имеют одинаковые угловые коэффициенты, либо совпадают.
Таким образом, с применением алгебраических выражений и свойств прямых мы можем доказать параллельность двух данных прямых ab и cd.
Доказательство с помощью свойств треугольников
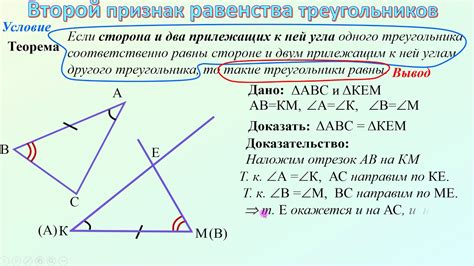
Доказательство параллельности прямых ab и cd может быть основано на свойствах треугольников.
- Сумма углов: Если сумма внутренних углов одного треугольника равна 180 градусов, то сумма внутренних углов другого треугольника тоже равна 180 градусов. Если прямая ab пересекает прямую cd, то образуется два треугольника: abc и cda. Если углы abc и cda равны, то сумма углов треугольников равна 180 градусов, и прямые ab и cd параллельны.
- Взаимная частность: Если прямая ab параллельна прямой cd, то соответствующие углы abc и cda равны. Это свойство позволяет нам доказать параллельность прямых, если мы можем найти две пары углов, которые равны.
- Постулат о параллельных линиях: Если прямая ab параллельна прямой cd и прямая bc пересекает прямую ab, то она также пересекает прямую cd. Это свойство используется для доказательства параллельности прямых с помощью третьей параллельной прямой.
Доказательство с использованием признаков параллельности

Для доказательства параллельности прямых ab и cd можно использовать различные признаки, основанные на их свойствах и характеристиках. В данном разделе рассмотрим несколько таких признаков.
1. Углы между прямыми. Если между прямыми ab и cd имеются пары соответственных углов, которые равны (например, углы a1 и c1, а также углы a2 и c2), то это является признаком их параллельности. Доказательство основывается на том, что если углы равны, то выполняются следующие соотношения: а1 + c1 = 180° и а2 + c2 = 180°. Если прямые ab и cd пересекаются, то сумма углов будет отличаться от 180°.
2. Отношение длин отрезков. Если отношение длин отрезков ab и bc равно отношению длин отрезков cd и da (то есть ab/bc = cd/da), то это может служить признаком параллельности прямых ab и cd. Обратное отношение (bc/ab = da/cd) также может использоваться для доказательства параллельности.
3. Перпендикулярные прямые. Если прямая ab перпендикулярна прямой cd, то это может служить признаком параллельности прямых ab и cd. Доказательство основывается на том, что перпендикулярные прямые имеют углы, равные 90°, и если прямая ab пересекает прямую cd, то эти углы будут отличаться от 90°.
4. Параллельный перенос. Если параллельные прямые ab и cd переносятся на равные расстояния в любом направлении, то это может служить признаком их параллельности. Доказательство основывается на том, что при параллельном переносе точки прямой смещаются на одинаковое расстояние и остаются на прямой.
Таким образом, признаки параллельности прямых ab и cd позволяют осуществить их доказательство. Использование этих признаков позволяет определить параллельность прямых на основе их свойств и характеристик, что может быть полезно при решении геометрических задач.