Параллелограмм - это геометрическая фигура, которая имеет особенности, делающие ее уникальной и интересной. Одной из таких особенностей является параллельность противоположных сторон. На первый взгляд, это может показаться простым и возможно даже очевидным фактом, но на самом деле параллельность сторон параллелограмма имеет глубокие и научно обоснованные причины.
Одной из ключевых причин параллельности противоположных сторон параллелограмма является его определение. Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны. Это определение предполагает, что у параллелограмма обязательно должны быть параллельные стороны. Отсюда становится понятно, что параллельность сторон является неотъемлемой и необходимой характеристикой этой геометрической фигуры.
Второй причиной параллельности противоположных сторон параллелограмма является его свойство быть как бы симметричным относительно диагоналей. Каждая диагональ параллелограмма делит его на две равные по площади части, которые зеркально отражены относительно этой диагонали. Такое симметричное расположение сторон и диагоналей делает противоположные стороны параллелограмма параллельными, а также является необходимым условием для наличия центра симметрии.
Параллелограмм: структура и свойства
Структура параллелограмма определяется его основными элементами:
| Сторона | Каждая из четырех сторон параллелограмма является отрезком, соединяющим две вершины. |
| Угол | Вершина параллелограмма образуется пересечением двух его сторон. Всего в параллелограмме четыре угла. |
| Диагональ | Диагональ – это отрезок, соединяющий две несмежные вершины параллелограмма. |
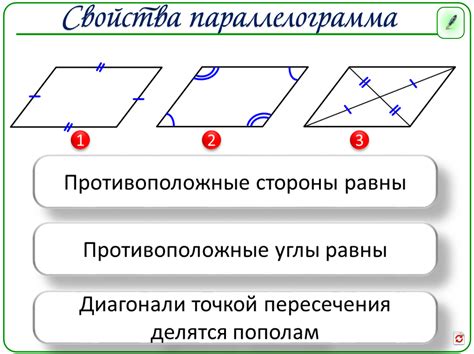
Свойства параллелограмма
Параллелограмм обладает следующими свойствами:
- Противоположные стороны параллельны и равны по длине.
- Противоположные углы параллелограмма равны.
- Сумма углов параллелограмма равна 360 градусов.
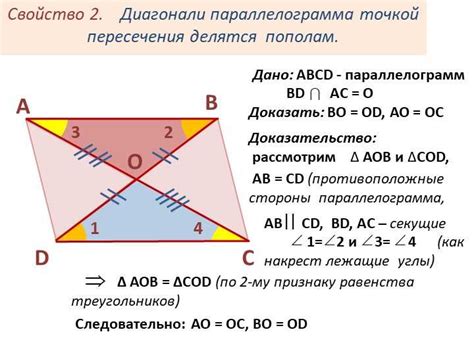
- Диагонали параллелограмма делятся пополам.
- Диагонали параллелограмма пересекаются в точке, которая делит их в одинаковом отношении.
Эти свойства позволяют с легкостью находить различные значения и отношения в параллелограммах, а также применять их в решении геометрических задач.
Что такое параллелограмм
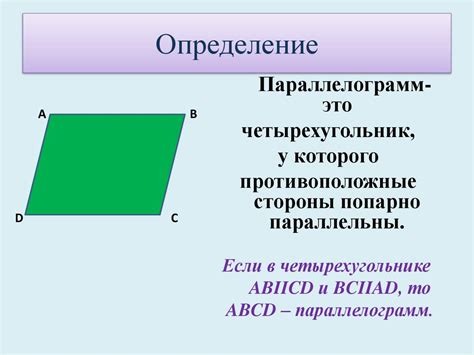
Основные характеристики параллелограмма:
- У него четыре стороны, противоположные стороны равны;
- Углы, образованные противоположными сторонами, равны;
- Диагонали параллелограмма делятся точкой пересечения пополам;
- Сумма углов параллелограмма равна 360 градусов.
Параллелограмм встречается в различных областях геометрии и имеет много применений в повседневной жизни. Он используется для построения и доказательства различных теорем, а также может быть использован в архитектуре, строительстве и дизайне для создания симметричных и гармоничных форм.
Какие стороны параллелограмма называются противоположными
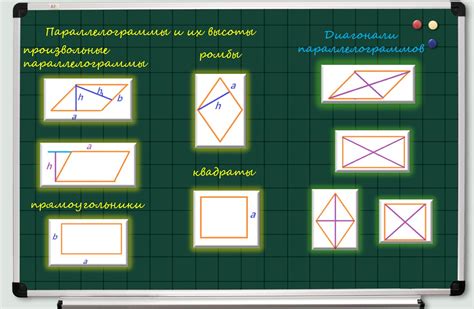
- Противоположные стороны параллелограмма называются основаниями.
- Две другие противоположные стороны называются боковыми сторонами.
Основания параллелограмма лежат напротив друг друга и имеют одинаковую длину. Они также являются параллельными линиями. В случае если параллелограмм является прямоугольником, основания будут равны длине и ширине прямоугольника.
Боковые стороны параллелограмма соединяют соответствующие вершины, не являющиеся соседними. Они тоже имеют одинаковую длину и параллельны друг другу. Боковые стороны параллелограмма имеют противоположное направление и располагаются параллельно основаниям.
Знание того, как называются противоположные стороны параллелограмма, помогает легче определять свойства и особенности этой геометрической фигуры, таких как углы, диагонали и периметр.
Причины параллельности противоположных сторон

Первой причиной параллельности противоположных сторон является определение параллелограмма. В определении четырехугольника, чтобы он считался параллелограммом, необходимо, чтобы обе пары противоположных сторон были параллельны. Таким образом, параллельность сторон является неотъемлемой и необходимой характеристикой параллелограмма.
Вторая причина связана с особенностями углов параллелограмма. В этой фигуре сумма противоположных углов всегда равна 180 градусам. Это происходит из-за свойства параллельных линий, которое говорит о том, что при пересечении прямых, образуемых сторонами параллелограмма, соответствующие углы равны. Таким образом, параллельность сторон приводит к равенству противоположных углов, что является еще одним фактором для параллельности сторон.
Третья причина параллельности противоположных сторон заключается в свойствах параллелограмма, связанных с его диагоналями. В параллелограмме диагонали делятся на две равные части и пересекаются в их точке деления. Это говорит о том, что диагонали параллелограмма обладают свойством симметрии относительно точки пересечения, а значит, стороны должны быть параллельны, чтобы сохранить эту симметрию.
Таким образом, параллельность противоположных сторон в параллелограмме обусловлена его определением, особенностями углов и свойствами диагоналей. Параллельность сторон является важным свойством этой геометрической фигуры и играет ключевую роль в их геометрических характеристиках и свойствах.
Свойства параллелограмма
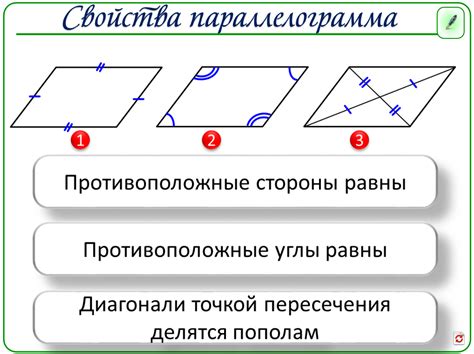
1. Противоположные стороны параллелограмма равны по длине.
2. Противоположные углы параллелограмма равны.
3. Сумма углов параллелограмма составляет 360 градусов.
4. Диагонали параллелограмма делятся пополам.
5. Диагонали параллелограмма взаимно перпендикулярны и делят фигуру на 4 равных треугольника.
Эти свойства помогают в решении различных задач, связанных с параллелограммами, например, нахождении площади или длины стороны. Также они позволяют упростить геометрические доказательства и нахождение неизвестных углов и сторон.
Применение параллелограмма в геометрии и архитектуре
В геометрии параллелограмм используется для доказательства и изучения свойств противоположных сторон, углов и диагоналей. Параллелограмм также является основой для изучения других фигур, таких как ромб, прямоугольник, и квадрат.
Кроме того, параллелограммы активно применяются в архитектуре. Многие знаменитые сооружения и здания имеют параллелограммальную форму, которая придает им уникальный и характерный вид. Параллелограммы используются для создания различных элементов архитектурных композиций – таких как фасады, окна, двери, балконы и т.д.
В архитектуре параллелограммы используются для создания перспективных эффектов и придания объектам гармоничной формы и пропорций. Эта геометрическая фигура позволяет архитекторам и дизайнерам воплотить свои идеи и концепции в жизнь, создавая уникальные и впечатляющие по своей архитектурной форме сооружения.
Таким образом, параллелограмм играет значимую роль в геометрии и архитектуре, используясь как инструмент для изучения и создания геометрических фигур, а также для придания объектам уникального вида и формы.