Системы счисления - это способы представления чисел с помощью определенного набора цифр и правил записи. Использование разных систем счисления позволяет выполнять различные математические операции и решать разнообразные задачи. Одним из важных аспектов в работе с системами счисления является перевод чисел из одной системы счисления в другую.
Перевод чисел из одной системы счисления в другую требует понимания принципов записи чисел в каждой системе счисления и использования соответствующих алгоритмов. Например, для перевода числа из десятичной системы счисления в двоичную можно использовать алгоритм деления числа на 2.
В данной статье мы рассмотрим основные системы счисления - двоичную, восьмеричную и шестнадцатеричную - и описывающие их правила записи чисел. Мы также рассмотрим алгоритмы перевода чисел из одной системы счисления в другую с примерами и пошаговым объяснением. Перевод чисел из одной системы счисления в другую является важным навыком для программистов и математиков, и овладение этим навыком поможет эффективнее работать с числами и выполнять сложные вычисления.
Перевод систем счисления
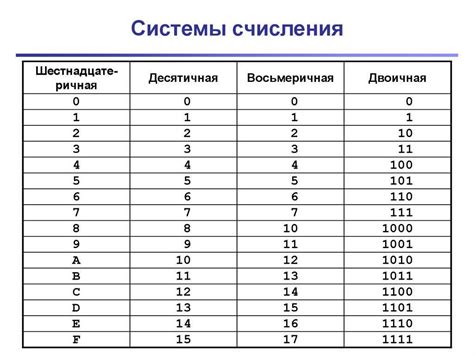
Перевод числа из одной системы счисления в другую может понадобиться в различных ситуациях. Например, при работе с программированием, компьютерными сетями, шифрованием данных и т. д. Важно понимать, как производить такие переводы и в каких случаях это необходимо.
Основные правила перевода числа из одной системы счисления в другую:
- Запишите заданное число в десятичной системе счисления.
- Разделите полученное число на основание целевой системы счисления и запишите остаток. Повторяйте этот шаг до тех пор, пока результат деления не станет равен 0.
- Запишите остатки в обратном порядке, начиная с последнего полученного остатка. Это будет представление заданного числа в целевой системе счисления.
Например, для перевода числа 101 из двоичной системы счисления в десятичную систему счисления, мы разобьем его на разряды: 1, 0 и 1. Затем, умножим каждый разряд на соответствующую степень двойки и сложим полученные произведения: 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 4 + 0 + 1 = 5. Таким образом, число 101 в двоичной системе счисления равно числу 5 в десятичной системе счисления.
Определение и цель
Основная цель перевода систем счисления - расширение возможностей представления чисел и работа с данными в различных областях, включая математику, информатику, программирование и электронику.
Понимание принципов и методов перевода систем счисления не только позволяет выполнять математические и логические операции с числами, но и помогает в улучшении навыков абстрактного мышления и решения задач разного уровня сложности.
| Система счисления | Описание | Примеры |
|---|---|---|
| Десятичная система | Система счисления с основанием 10. Использует цифры от 0 до 9. | 123, 456, 789 |
| Двоичная система | Система счисления с основанием 2. Использует цифры 0 и 1. | 1010, 1101, 1110 |
| Восьмеричная система | Система счисления с основанием 8. Использует цифры от 0 до 7. | 234, 567, 712 |
| Шестнадцатеричная система | Система счисления с основанием 16. Использует цифры от 0 до 9 и буквы A-F. | 1A3, 4D6, C17 |
В данной статье мы рассмотрим основные принципы перевода чисел из одной системы счисления в другую, а также представим конкретные примеры для лучшего понимания процесса.
Десятичная система счисления
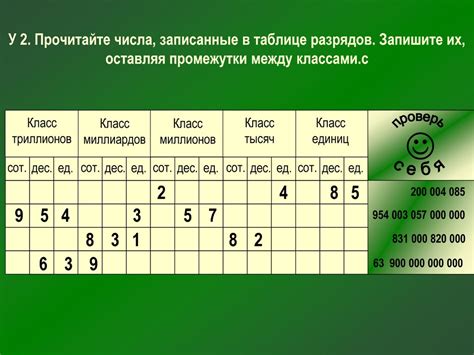
Всем нам хорошо знакома десятичная система счисления, так как мы ежедневно используем ее для работы с числами. Она основана на том, что у нас есть десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
В десятичной системе каждая позиция числа имеет вес, который определяется ее расположением от точки. Самая правая позиция имеет вес 1, следующая - 10, затем - 100, и так далее. Например, число 357 может быть разложено на сумму 3 * 100 + 5 * 10 + 7 * 1.
Десятичная система широко используется в повседневной жизни, а также во многих областях, включая науку, финансы и программирование. Она является основной системой счисления для большинства людей.
При переводе чисел из других систем счисления в десятичную систему счисления необходимо знать значение каждой цифры в соответствующей системе. Это позволяет умножать цифры на соответствующую степень основания системы счисления и складывать полученные произведения.
Например, чтобы перевести число 101 из двоичной системы счисления в десятичную, мы умножаем каждую цифру на 2 в степени позиции: 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 5.
Десятичная система счисления позволяет нам удобно работать с числами, и она является основой для изучения других систем счисления.
Двоичная система счисления
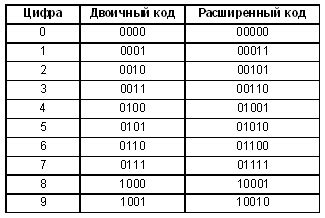
Двоичная система счисления широко применяется в компьютерах и цифровой электронике, так как легко представляет двоичное кодирование, в котором информация представляется в виде последовательности битов. Это основа для работы сигналов в цифровых системах и позволяет обрабатывать информацию в компьютерах с использованием логического арифметического.
В двоичной системе счисления цифры увеличиваются в два раза, а разряды чисел увеличиваются в степени двойки. Например, число 101 в двоичной системе счисления представляет собой 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 5 в десятичной системе счисления. Переход от двоичной системы к десятичной можно производить путем умножения каждой цифры на соответствующую степень двойки и сложения полученных результатов.
Двоичная система счисления также имеет свою таблицу умножения, аналогичную десятичной системе. Она полезна при выполнении операций умножения и деления в двоичной системе счисления. Также существует возможность перевода чисел из двоичной системы в другие системы счисления, такие как десятичная, восьмеричная или шестнадцатеричная, используя соответствующие формулы и таблицы перевода.
Двоичная система счисления является основой для работы с информацией в компьютерах и цифровой электронике. Понимание принципов двоичной системы счисления позволяет осуществлять операции с двоичными числами и понимать, как числа и данные представлены и обрабатываются в этих системах.
Восьмеричная система счисления
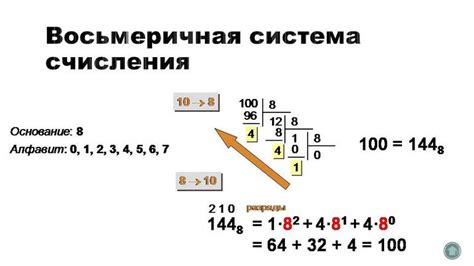
Восьмеричная система счисления, также известная как октальная система, это позиционная система счисления, основанная на числе 8. В этой системе используются цифры от 0 до 7.
Восьмеричная система широко применяется в информатике и программировании, так как в ней легко представлять двоичные числа. Три восьмеричные цифры составляют вместе одну цифру в двоичной системе, что делает ее более компактной.
Чтобы перевести число из десятичной системы счисления в восьмеричную, следует разделить число на 8 и записать остатки от деления снизу вверх. Затем остатки объединяются вместе и дают искомое число в восьмеричной системе.
К примеру, число 75 в десятичной системе может быть записано как 113 в восьмеричной системе, так как 7 * 8^2 + 1 * 8^1 + 3 * 8^0 = 64 + 8 + 3 = 75.
Восьмеричные числа иногда представляются с приставкой "0o" для обозначения их системы счисления. Например, 0o113 представляет число 75 в восьмеричной системе.
Восьмеричная система счисления может быть очень полезной в программировании и информатике, особенно при работе с битовыми операциями и представлением чисел в двоичной системе.
Шестнадцатеричная система счисления

Для обозначения чисел в шестнадцатеричной системе вместо обычных арабских цифр используются соответствующие буквы и цифры. Например, число 10 обозначается буквой A, число 11 – буквой B и так далее.
Перевод чисел из десятичной системы в шестнадцатеричную осуществляется методом последовательного деления на 16. Остатки при делении в соответствии с таблицей перевода заменяются на соответствующие им символы. Операция повторяется до тех пор, пока результат деления не станет меньше 16.
Например:
- Давайте переведем число 250 в шестнадцатеричную систему:
- 250 / 16 = 15 (остаток: 10, A)
- 15 / 16 = 0 (остаток: 15, F)
На самом деле, в языках программирования шестнадцатеричные числа часто обозначаются с префиксом 0x. Например, число 250 можно записать как 0xFA.
Правила перевода из одной системы в другую

Перевод чисел из одной системы счисления в другую требует выполнения определенных правил и шагов. Ниже представлены основные указания, которые помогут вам освоить этот процесс:
1. Определите системы счисления: Перед тем как начать перевод, убедитесь, что вы знаете, из какой системы счисления вы переводите и в какую систему счисления вы переводите.
2. Определите числа: Определите число, которое вы хотите перевести, и убедитесь, что оно представлено в правильной системе счисления. Если оно записано неправильно, переведите его.
3. Запишите разряды: Запишите числа каждого разряда отдельно. Например, разряды числа 123 в десятичной системе счисления будут следующими: 1, 2, 3.
4. Назначьте вес разрядов: Назначьте вес каждому разряду. Вес разрядов определяется позицией разряда от правой стороны числа, начиная с 0. Например, в числе 123 вес разряда 2 будет равен 1, вес разряда 1 будет равен 10, а вес разряда 0 будет равен 100.
5. Выполните умножение: Умножьте каждое число в разрядах на его вес. Например, для числа 123 в десятичной системе счисления результаты будут следующими: разряд 2 умножаем на 1, разряд 1 умножаем на 10, и разряд 0 умножаем на 100.
6. Просуммируйте результаты: Просуммируйте все результаты умножения, чтобы получить итоговое число в целевой системе счисления.
7. Выпишите итоговое число: Запишите итоговое число в целевой системе счисления и убедитесь, что оно записано правильно.
Эти правила помогут вам в освоении процесса перевода чисел из одной системы счисления в другую. Практикуйтесь и углубляйтесь в изучение данной темы, чтобы стать более уверенным в этом навыке.
Примеры перевода

Рассмотрим несколько примеров перевода чисел между различными системами счисления:
Пример 1:
Десятичное число 15 в двоичной системе счисления:
1510 = 11112
Пример 2:
Десятичное число 217 в шестнадцатеричной системе счисления:
21710 = D916
Пример 3:
Двоичное число 1101 в десятичной системе счисления:
11012 = 1310
Пример 4:
Шестнадцатеричное число 3F в двоичной системе счисления:
3F16 = 1111112
Это лишь некоторые из множества возможных примеров перевода чисел между системами счисления. Надеемся, что эти примеры помогут вам лучше понять процесс перевода и применение различных систем счисления в реальной жизни.
Значение перевода систем счисления в компьютерах
Перевод из десятичной системы счисления в двоичную позволяет компьютеру эффективно представлять числа и выполнять различные операции с ними. Например, при работе с текстовыми данными, каждая буква может быть представлена в виде двоичного кода, что позволяет компьютеру обрабатывать и отображать текст. Также перевод систем счисления используется при решении математических задач, алгоритмах и арифметических операциях, таких как сложение, вычитание, умножение и деление.
Другим примером использования перевода систем счисления является работа с изображениями. Каждый пиксель изображения может быть представлен в виде чисел, которые также могут быть переведены в двоичную систему счисления. Это позволяет компьютеру сохранять и обрабатывать изображения с высокой точностью.
В общем, перевод систем счисления играет важную роль в компьютерах, позволяя им представлять и обрабатывать данные различных типов. Это фундаментальное понятие, которое является основой для понимания работы компьютеров и программирования.
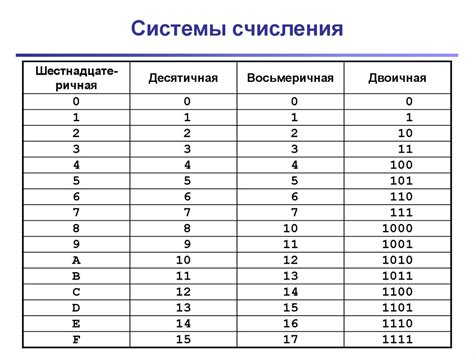
| Десятичная система | Двоичная система |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |