В мире математики мы привыкли доверять числам и операциям, которые над ними выполняются. Однако, как бы странно это ни звучало, в ряде случаев при решении примеров возникают ошибки.
Именно вопрос о том, почему 2 плюс два равно 5, является одним из таких примеров. Несмотря на то, что большинство из нас знает, что результат этой операции составляет 4, иногда люди совершают ошибки и получают неправильный ответ.
Ошибки в математических вычислениях могут возникать из-за различных причин: неверного применения правил операций, пропуска необходимых шагов, пренебрежения десятичными знаками и др. Ошибочное решение примера "2 + 2" равно 5 может служить примером такого неверного подхода к математическим задачам.
Почему результат 2 плюс два равен 5?
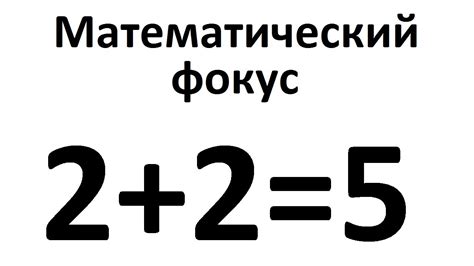
Видимо, в примере "2 плюс два равно 5" допущена ошибка в математической операции сложения. Правильно решение этого примера будет следующим:
- Сначала необходимо преобразовать слово "два" в числовое значение 2.
- После этого нужно сложить числа 2 и 2, получив в результате число 4.
- Таким образом, правильный ответ на пример "2 плюс два" будет равен 4, а не 5.
Ошибочное решение примера "2 плюс два равно 5" может быть обусловлено неверным пониманием математических операций либо невнимательным выполнением расчетов. Чтобы избежать подобных ошибок, важно внимательно читать и понимать условия задачи, а также правильно выполнять математические операции.
Знаки и их значения
Знаки математических операций, такие как плюс (+), минус (-), умножить (×) и делить (÷), играют важную роль в математике. Они обозначают определенные действия, которые нужно выполнить с числами.
Плюс (+) используется для сложения двух или более чисел. Например, 2 + 2 = 4. Этот оператор позволяет суммировать значения и получать результат.
Минус (-) обозначает вычитание одного числа из другого. Например, 5 - 3 = 2. Этот оператор позволяет находить разницу между значениями.
Умножить (×) используется для умножения чисел. Например, 3 × 4 = 12. Этот оператор позволяет получать произведение значений.
Делить (÷) обозначает деление числа на другое число. Например, 10 ÷ 2 = 5. Этот оператор позволяет находить частное значений.
В математике есть строго установленные правила, как использовать эти знаки, и решение примера 2 + 2 = 5 является ошибочным, поскольку истинное значение этого примера равно 4.
Ошибка при сложении

Одним из наиболее известных примеров такой ошибки является утверждение, что "2 плюс два равно 5". Это является абсолютно неверным утверждением, которое противоречит базовым математическим правилам сложения. Ошибки в данном примере могут возникать по разным причинам, включая недостаток внимания, неправильное понимание математического символа "+" или неправильное расчетное действие.
Чтобы избежать подобных ошибок, важно внимательно читать и понимать постановку задачи, правильно интерпретировать математические символы и внимательно выполнять расчетные операции. Также полезно проводить дополнительную проверку результатов, чтобы убедиться в их правильности. Ошибка при сложении, как и любая другая ошибка, может быть исправлена с помощью дополнительного изучения и практики.
Математическое противоречие

Одним из примеров такого противоречия является утверждение, что 2 плюс 2 равно 5. Правильный ответ на этот пример, согласно математическим правилам, составляет 4. Однако, некоторые люди могут сделать ошибку в вычислениях или использовать неправильные математические операторы, что приведет к неверному результату.
Математическое противоречие может возникнуть по нескольким причинам. Первая причина - это неправильное применение математических операторов. Например, если мы сложим числа 2 и 2, то получим 4, но если прибавить к этому результату еще 1, то получим 5. Это связано с неправильным использованием оператора сложения.
Вторая причина может быть связана с ошибками в самом составлении примера. Например, если изначально были указаны неправильные числа или операторы, то полученный результат может быть неверным. В случае с примером 2 плюс 2 равно 5, сама постановка примера является ошибочной и вводит в заблуждение.
Некоторые люди могут считать, что математическое противоречие возникает вследствие особенностей округления чисел или других арифметических правил. Однако, это не так. Математический противоречие означает нарушение одного или нескольких основных математических законов, что делает результат недостоверным и неправильным.
Поэтому, при решении любых математических задач и примеров, необходимо придерживаться строгих математических правил и правильно применять операторы. Это избавит нас от возможных ошибок и математических противоречий.
Психологические аспекты
Человек часто подвержен влиянию своих предубеждений и стереотипов, которые могут искажать его восприятие реальности. В случае с математическим уравнением 2+2=5, ошибка может возникнуть из-за неправильного понимания понятий, негативного опыта или простого непосредственного вмешательства окружающих.
Также, психологические и когнитивные искажения, такие как иллюзорная корреляция или эффект подтверждения, могут влиять на способность человека анализировать и решать математические задачи. Когда мы имеем определенные ожидания или представления, мы можем проигнорировать факты, которые не совпадают с ними, или же неправильно интерпретировать информацию, чтобы она подтвердила наши предубеждения.
Более того, психологические аспекты, связанные с эмоциональным состоянием человека, также могут влиять на его способность анализировать и решать задачи. Стресс, тревога или усталость могут снижать концентрацию и умственные возможности, что может привести к ошибкам в решении простых уравнений.
Итак, ошибочное решение примера 2+2=5 можно рассматривать не только как математический промах, но и как иллюстрацию психологических факторов, которые могут влиять на нашу способность анализировать и решать задачи. Правильное понимание и осознание этих факторов помогает нам избегать подобных ошибок и повысить нашу математическую и психологическую грамотность.
Правильное решение

Правильное решение примера "2 плюс два равно 5" связано с арифметическими законами и математическими операциями.
В арифметике существуют определенные правила, которые позволяют нам точно определить результаты математических операций. Например, закон коммутативности утверждает, что порядок слагаемых при сложении может быть изменен, но результат останется неизменным.
Если мы применим этот закон к примеру "2 плюс 2", то получим: 2 + 2 = 4. Таким образом, правильное математическое решение примера "2 плюс 2 равно 5" будет равно 4, а не 5.
Также существует еще один важный закон - закон ассоциативности, который утверждает, что результат сложения не зависит от способа группировки слагаемых. Например, выражение (2 + 2) + 1 будет давать тот же результат, что и 2 + (2 + 1) - то есть 5.
Таким образом, правильное математическое решение примера "2 плюс 2 плюс 1 равно 5" будет равно 5 при учете закона ассоциативности.



