Алгебра логики – это раздел математики, изучающий математические структуры и операции, которые связаны с логическими высказываниями. Она получила такое название в честь математика и логика Джорджа Буля, который впервые разработал систему символов и правил для описания логических операций и высказываний.
Булева алгебра играет важную роль в информатике, теории вычислений и электронике. Она основывается на двух основных логических значениях: истина (1) и ложь (0). В булевой алгебре используются операции конъюнкции (логическое "и"), дизъюнкции (логическое "или") и отрицания (логическое "не"). Эти операции позволяют строить сложные выражения и анализировать логические законы и отношения.
Булева алгебра была разработана для решения логических проблем и создания вычислительных устройств, которые могут обрабатывать информацию в виде двоичного кода. Она является основой для цифровой электроники и компьютерных наук. Булева алгебра также находит применение в базах данных, сетевых протоколах, криптографии и других областях, где важны логические операции и вычисления.
Что такое алгебра логики и почему она называется булевой алгеброй?
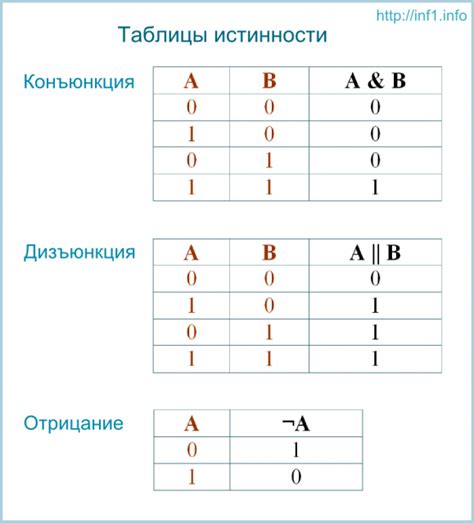
Алгебра логики получила свое название в честь Джорджа Буля, который впервые разработал систему символов и операций, носящую его имя. Булева алгебра - это система логического анализа, основанная на двух возможных значениях: истина (1) и ложь (0). Основные операции Булевой алгебры - это конъюнкция, дизъюнкция и отрицание, которые соответствуют логическим операциям "И", "ИЛИ" и "НЕ".
Алгебра логики имеет широкое применение в различных областях, таких как вычислительная техника, информатика, электроника, кибернетика и другие. Она позволяет строить и анализировать логические схемы, создавать логические функции и управлять ими. Благодаря своей простоте и эффективности, булева алгебра стала основой для развития современных компьютеров и систем связи.
Таким образом, алгебра логики, или булева алгебра, играет важную роль в различных областях науки и техники, предоставляя формальные методы и инструменты для анализа и работы с логическими операциями и выражениями.
Определение алгебры логики

Основные элементы алгебры логики – это логические операции, которые позволяют комбинировать высказывания и получать новые высказывания на основе старых. Примерами таких операций являются конъюнкция (логическое "И"), дизъюнкция (логическое "ИЛИ") и отрицание (логическое "НЕ").
Алгебра логики также включает в себя утверждения о свойствах этих операций, а также способы их использования. Она широко применяется в различных областях, таких как информатика, электроника и философия.
- Логические операции позволяют выразить сложные высказывания в виде комбинаций простых высказываний.
- Утверждения алгебры логики могут быть проверены и применены с использованием алгоритмов и таблиц истинности.
- Алгебра логики является основой для построения логических систем и языков программирования, а также для создания цифровых схем и логических устройств.
Термин "булева алгебра" обозначает связь алгебры логики с именем математика и логика Джорджа Буля, который разработал основные принципы исчисления логики в 1854 году. Благодаря его исследованиям алгебра логики получила широкое признание и нашла применение в многих научных и практических областях.
История развития алгебры логики

Однако идеи, лежащие в основе алгебры логики, имеют гораздо более древние корни. Уже в античности философы, такие как Аристотель, занимались логическими расчетами и классификацией утверждений. Он определил несколько логических операций, таких как «И», «ИЛИ» и «НЕ», которые стали основой для дальнейшего развития логики.
С развитием математики в XIX и XX веках алгебра логики стала более формализованной и получила аксиоматический подход, а в 20-м веке ее основы были формализованы и аксиоматизированы в работах математиков, таких как Джордж Боол, Кристиану Бернсайду, Давиду Гильберту и другими.
Сейчас алгебра логики широко применяется в различных областях, таких как информатика, электроника, философия и правоведение. Она помогает анализировать и изучать формальные системы, строить компьютерные схемы и разрабатывать различные алгоритмы решения проблем.
Таким образом, история развития алгебры логики свидетельствует о том, что она является результатом долгой эволюции и внесла значительный вклад в развитие математики и других наук.
Какова роль алгебры логики в информатике?
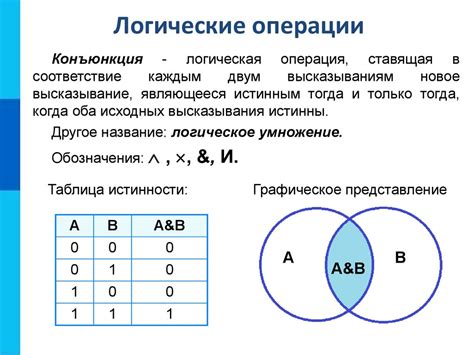
Алгебра логики предоставляет набор правил и операций, которые позволяют выполнять логические операции над символами и значениями. Она устанавливает основы для создания и анализа логических выражений, которые в дальнейшем используется в различных областях информатики, таких как цифровая логика, компьютерные сети, базы данных, искусственный интеллект и другие.
Одно из ключевых применений алгебры логики в информатике - разработка и оптимизация логических схем и схемного описания цифровых устройств. Алгебра логики позволяет строить и анализировать логические функции, которые являются основой для конструирования цифровых схем. Это важное звено в проектировании компьютерных систем и устройств.
Кроме того, алгебра логики применяется в разработке алгоритмов и программировании. Логические операции и выражения являются основой для построения логических условий и логических операторов в программировании. Алгебра логики позволяет формализовать и решать логические задачи в программировании, например, проверку условий и установку логических связей между данными и операциями.
Таким образом, алгебра логики играет важную роль в информатике, предоставляя средства для представления, анализа и обработки логических значений. Она является фундаментальным инструментом для разработки логических систем и алгоритмов, а также является основой для построения логических вычислений и операций в информационных системах.
Применение алгебры логики в технике и телекоммуникациях

Одним из основных способов применения алгебры логики является проектирование и анализ цифровых схем. Цифровые схемы состоят из логических элементов, таких как вентили, которые могут осуществлять логические операции с двоичными данными. Алгебра логики позволяет решать задачи проектирования и оптимизации этих схем путем анализа и преобразования логических выражений.
Алгебра логики также находит применение в разработке и анализе алгоритмов. Логические операции, такие как конъюнкция, дизъюнкция и отрицание, используются для моделирования условий и логических выражений в программировании. Алгебра логики позволяет проводить анализ алгоритмов, проверять их корректность и эффективность.
В области телекоммуникаций алгебра логики используется для разработки и анализа протоколов и сетей. Логические операции позволяют моделировать поведение и коммуникацию устройств и систем, а алгебра логики помогает провести анализ и оптимизацию этих систем.
Таким образом, применение алгебры логики в технике и телекоммуникациях играет важную роль в разработке и оптимизации систем, устройств, алгоритмов, протоколов и сетей. Это позволяет повысить эффективность, надежность и безопасность различных технических решений и обеспечить их соответствие логическим и алгоритмическим требованиям.



