Алгебра логики – важная область математики, которая изучает принципы и методы работы с логическими выражениями и символами. Одним из ключевых моментов в алгебре логики является выбор системы численности для представления данных. Во многих случаях алгебра логики выбирает двоичную систему численности, и это имеет свои веские причины.
Двоичная система численности основана на использовании всего двух цифр – 0 и 1, в отличие от десятичной системы, которая использует 10 цифр. Это делает двоичную систему особенно удобной для алгебры логики. По сути, двоичные числа могут быть представлены как истинностные значения – 0 означает ложь, а 1 – истину. Это позволяет использовать двоичную систему для анализа и моделирования логических выражений и операций.
Выбор двоичной системы численности также связан с реализацией электронных устройств. В компьютерах и других электронных схемах информация представлена в виде двоичных чисел. Логические операции, такие как сложение или умножение, выполняются на микроуровне с использованием электрических сигналов, которые могут быть представлены двумя состояниями – напряженным и нет. Именно поэтому двоичная система численности является основной системой в электронике и компьютерных науках.
Влияние алгебры логики на выбор двоичной системы численности
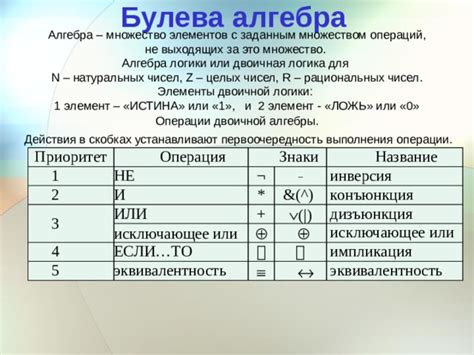
Причина выбора двоичной системы численности в алгебре логики связана с простотой и надежностью такой системы. Двоичная система основана на двух цифрах, 0 и 1, которые могут представлять логические значения: ложь и истину, соответственно.
Использование двоичной системы численности позволяет упростить логические операции и упрощает проектирование электронных устройств. Кроме того, двоичная система легко реализуется в электронных схемах, где 0 обозначает отсутствие напряжения, а 1 - его присутствие. Это делает двоичную систему идеальной для представления информации в компьютерах.
Бинарное кодирование информации также имеет преимущества при передаче и хранении данных. Двоичные числа занимают меньше места и легче обрабатываются электронными устройствами. Более того, двоичная система обеспечивает надежность передачи данных, так как ее значения лучше сохраняются и восстанавливаются при ошибках.
Таким образом, выбор двоичной системы численности в вычислительной технике основан на простоте и надежности этой системы, а также ее легкой реализации в электронных устройствах. Алгебра логики сыграла ключевую роль в развитии и применении данной системы, что позволило создать современную компьютерную технологию и информационные системы.
Разрабатывая логические системы
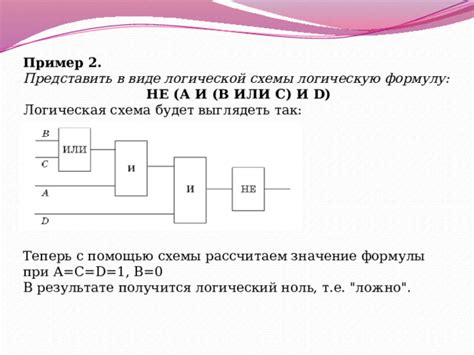
Двоичная система численности основана на двух цифрах - 0 и 1, и отличается от десятичной системы, которая основана на десяти цифрах - от 0 до 9. Почему именно двоичная система была выбрана в алгебре логики?
Основная причина выбора двоичной системы численности связана с простотой и удобством ее применения. В алгебре логики используются два основных логических значения - истина (1) и ложь (0). Эти значения могут быть представлены с помощью двух состояний - например, включено (1) и выключено (0), открыто (1) и закрыто (0), или любые другие противоположные состояния.
Двоичная система численности также имеет математическое обоснование. Она основана на принципах булевой алгебры, которая является основой алгебры логики. Булева алгебра исследует логические операции, такие как "и", "или" и "не", и определяет правила их применения. Она позволяет выражать любую логическую функцию в терминах логических операций и логических переменных, которые могут принимать значения 0 или 1.
| Логическое значение | Десятичное представление | Двоичное представление |
|---|---|---|
| Ложь | 0 | 0 |
| Истина | 1 | 1 |
Таким образом, двоичная система численности обладает простотой, удобством применения и математической обоснованностью, что делает ее идеальным выбором для алгебры логики. Она позволяет проводить операции и выражать различные логические функции с помощью всего двух логических значений, что делает алгебру логики мощным и эффективным инструментом для анализа и разработки логических систем.
Применение в электронике

В электронных схемах используются логические элементы, такие как вентили, которые выполняют различные логические операции с двоичными сигналами. Алгебра логики позволяет анализировать, проектировать и оптимизировать такие схемы.
Применение алгебры логики в электронике также расширяется на программное обеспечение. Булевы значения, которые основываются на двоичной системе численности, используются для логического программирования и создания алгоритмов.
Таким образом, выбор двоичной системы численности в алгебре логики обусловлен не только естественной природой электронных устройств, но и удобством анализа и обработки двоичной информации.
Избежание ошибок при передаче данных

При передаче данных возможны различные ошибки, такие как искажение сигнала, помехи на линии связи или ошибки при чтении данных. Однако, двоичная система имеет ряд преимуществ, которые помогают избежать этих ошибок и обеспечить надежность передачи информации.
Во-первых, двоичная система обладает простой и четкой структурой. Она использует всего два символа - 0 и 1, что упрощает процесс распознавания и чтения информации. Также эта система легко масштабируется, что позволяет передавать данные с высокой скоростью и обрабатывать их эффективно.
Во-вторых, двоичная система позволяет исправлять ошибки при передаче данных. Путем добавления дополнительной контрольной суммы или проверочных битов, можно обнаружить и исправить ошибки, возникшие в процессе передачи информации.
Ещё одним преимуществом двоичной системы является её устойчивость к помехам на линиях связи. В отличие от других систем, которые используют больше символов или аналоговые сигналы, двоичная система более устойчива к искажению и помехам.
В итоге, выбор двоичной системы численности в алгебре логики обусловлен её удобством, надёжностью и простотой обработки данных. Она позволяет избежать ошибок при передаче информации и обеспечить точность и надёжность всех операций.
Простота реализации и вычислений

Двоичная система также обладает преимуществами в реализации цифровых схем, таких как компьютеры. В компьютерах информация хранится и обрабатывается в виде битов - двоичных цифр. Использование двоичной системы позволяет легко представлять числа, исполнять арифметические операции и логические вычисления. Бинарные коды также применяются в множестве других областей, таких как телекоммуникации, электроника и криптография.
Математическая основа двоичной системы численности позволяет точно определить и вычислить все возможные значения переменных и выполнить логические операции. Благодаря этой простоте, алгебра логики находит широкое применение в различных областях науки и техники.
Совместимость с физическими системами
Двоичная система численности, выбранная алгеброй логики, обладает высокой совместимостью с физическими системами. Это связано с тем, что многие физические системы имеют два состояния, например, включено/выключено, присутствует/отсутствует, да/нет.
Двоичная система численности позволяет удобно представить и обрабатывать информацию в таких системах. Например, в цифровых электронных схемах сигналы в компьютере представлены двумя уровнями напряжения - высоким и низким. Это соответствует цифрам 1 и 0 в двоичной системе численности.
Также двоичная система численности широко используется в аппаратуре и программном обеспечении для обработки и хранения данных. Бинарные коды позволяют эффективно представлять и передавать информацию, а операции логического И, ИЛИ, НЕ, выполняемые на двоичных данных, дают возможность логическим вычислениям и контролю.
Все это делает двоичную систему численности и алгебру логики неотъемлемой частью современной электроники, компьютерных наук и информационных технологий. Они позволяют эффективно работать с физическими системами и обрабатывать информацию, что является основой для создания сложных технических устройств и программных систем.
Принципы работы компьютерных систем

Компьютерные системы основаны на принципах алгебры логики и используют двоичную систему численности для своей работы. В этой системе числа представлены двумя символами: 0 и 1. Двоичная система выбрана по ряду причин.
Первая причина – простота. Двоичная система счета обладает простыми правилами, что упрощает процесс обработки чисел компьютером. Все операции, которые производит компьютер, основаны на принципе двоичной алгебры.
Вторая причина – надежность. Использование двух символов для представления чисел позволяет уменьшить вероятность возникновения ошибок при передаче информации. Компьютеры способны обнаруживать и исправлять ошибки благодаря использованию специальных кодов, таких как код Хэмминга.
Третья причина – масштабируемость. Двоичная система численности позволяет компьютерам легко масштабироваться. Система может быть масштабирована путем добавления дополнительных битов или повышения их разрядности. Это позволяет компьютеру обрабатывать все больше и больше информации.
Четвертая причина – совместимость. Множество компьютерных систем и электронных устройств работают на основе двоичной системы численности. Это обеспечивает совместимость и возможность обмена данных между разными устройствами. Благодаря этому, компьютеры могут взаимодействовать друг с другом и выполнять различные задачи.
Таким образом, выбор двоичной системы численности в алгебре логики и компьютерных системах обусловлен простотой, надежностью, масштабируемостью и совместимостью. Эти принципы обеспечивают эффективную и надежную работу компьютерных систем и позволяют им выполнять широкий спектр задач.



