Четырехугольник abcd - это геометрическая фигура, образованная четырьмя отрезками, которые соединяются по своим концам. Однако, не все четырехугольники имеют одну и ту же форму и свойства. И вот почему четырехугольник abcd не является трапецией.
Трапецией называется четырехугольник, у которого два противоположных отрезка параллельны между собой. В четырехугольнике abcd, отрезки ab и cd не являются параллельными. Это значит, что их стороны не будут когда-либо располагаться строго параллельно друг другу.
Кроме того, в трапеции основания - это параллельные стороны, а боковые стороны - это наклонные стороны. Однако, в четырехугольнике abcd, стороны ad и bc не соответствуют этим характеристикам. Вместо этого они являются наклонными сторонами, что делает четырехугольник abcd отличным от трапеции.
Таким образом, четырехугольник abcd не является трапецией из-за отсутствия параллельности его отрезков ab и cd, а также из-за неправильных соотношений между сторонами ad и bc. Понимание этих особенностей позволяет нам различать разные геометрические фигуры и определять их свойства.
Свойства четырехугольников

- Сумма внутренних углов четырехугольника всегда равна 360 градусов. Независимо от формы и размеров сторон, углы четырехугольника всегда будут в сумме давать 360 градусов.
- Если четырехугольник является выпуклым, то его диагонали – это отрезки, соединяющие его вершины, которые не являются соседними. Диагонали выпуклого четырехугольника пересекаются внутри фигуры и делят ее на четыре треугольника.
- Если четырехугольник является пересекающимся, то его диагонали пересекаются вне фигуры, и он также делится на четыре треугольника.
- Четырехугольник может быть выпуклым или невыпуклым. Выпуклый четырехугольник все свои вершины смотрит в одну сторону – внутрь или вовне фигуры. Невыпуклый четырехугольник имеет хотя бы одну вершину, обращенную внутрь фигуры.
На основании этих свойств можно провести классификацию четырехугольников. Например, в рамках данной статьи мы установили, что четырехугольник abcd не является трапецией, так как он имеет диагонали, пересекающиеся внутри фигуры и не являющиеся параллельными сторонам. Это пример пересекающегося четырехугольника.
Что такое трапеция
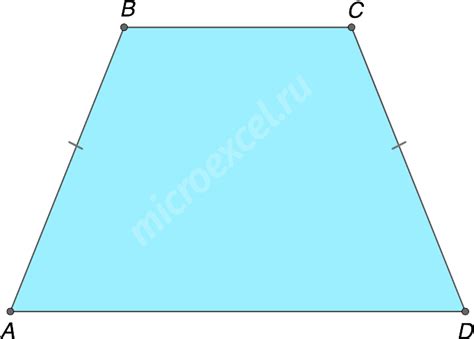
Трапецией называется выпуклый четырехугольник, у которого две противоположные стороны параллельны. Такие стороны называются основаниями трапеции. Остальные две стороны называются боковыми сторонами.
Основания трапеции обычно обозначают буквами a и b. Боковые стороны обозначаются буквами c и d. Одна из боковых сторон (обычно большая) называется высотой трапеции.
Для того чтобы четырехугольник мог быть назван трапецией, необходимо, чтобы выполнялось условие параллельности оснований. Если стороны ab и cd не являются параллельными, то четырехугольник abcd не может быть трапецией.
Стороны и углы четырехугольника abcd
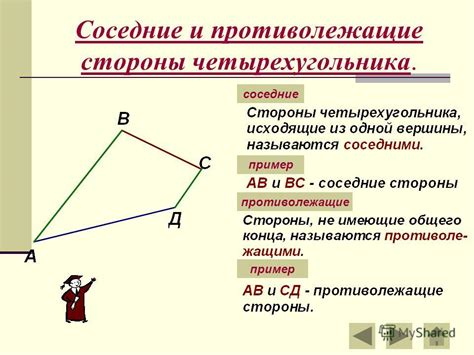
Стороны ab и cd параллельны, так как они лежат на одной прямой и не пересекаются. Стороны bc и da не параллельны.
Угол abc и угол cda не являются смежными и не равны между собой. Углы abd и cdb также не являются смежными и не равны друг другу.
Таким образом, исходя из определения трапеции, которая имеет только две параллельные стороны и две основания, четырехугольник abcd не является трапецией.
| Сторона | Длина |
|---|---|
| ab | ... |
| bc | ... |
| cd | ... |
| da | ... |
Особенности сторон и углов трапеции
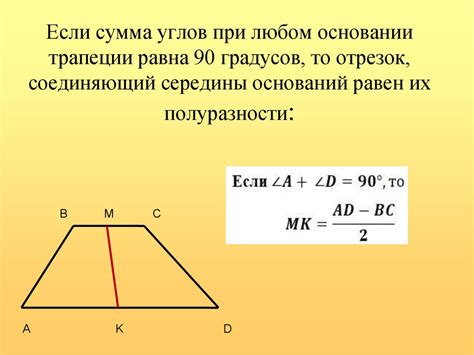
Если присмотреться к трапеции, то можно заметить, что диагонали трапеции не равны друг другу. Одна из диагоналей является большей, а другая - меньшей. Это свойство отличает трапецию от прямоугольника, у которого диагонали равны друг другу.
Еще одна особенность трапеции заключается в том, что сумма углов, лежащих на одном основании, равна 180 градусам. То есть углы a и c вместе дают прямой угол. Это следует из свойства, что сумма углов треугольника равна 180 градусам.
Также стоит отметить, что два угла, лежащие на одной боковой стороне, называются смежными. Эти углы дополняют друг друга до прямого угла.
Сравнение сторон и углов abcd и трапеции
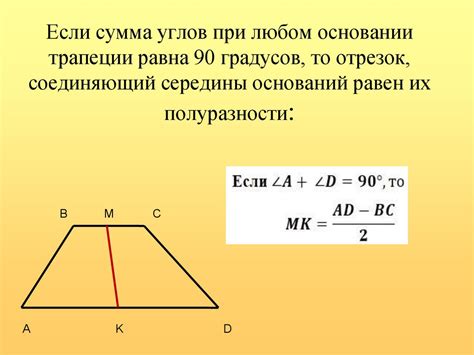
Трапеция - четырехугольник, у которого две стороны параллельны и две другие стороны не параллельны. Другими словами, одна пара сторон параллельна, а другая пара - нет.
В случае четырехугольника abcd необходимо проверить, выполняются ли эти условия.
Столкнемся с тем, что все стороны четырехугольника abcd представляют собой отрезки, которые могут быть восстановлены с помощью линейки.
Итак, углы abcd. Предположим, что ab параллельна cd, тогда мы также предполагаем, что ad и bc не являются параллельными.
У нас есть две пары противоположных углов: abd и bcd, adc и cda. Если abcd является трапецией, то углы abd и bcd должны быть прямыми, а углы adc и cda должны быть дополнительными.
Однако, при изучении собственных углов четырехугольника abcd, мы обнаружим, что ни один из углов не является прямым, а углы adc и cda не являются дополнительными. Таким образом, условия, определяющие трапецию, не выполняются в случае четырехугольника abcd.
Исходя из этого, мы можем заключить, что четырехугольник abcd не является трапецией.
- Четырехугольник abcd не является трапецией, так как он не имеет параллельных сторон.
- Сторона ab не параллельна стороне cd и не равна ей по длине.
- Сторона bc не параллельна стороне da и не равна ей по длине.
- Сторона cd не параллельна стороне ab и не равна ей по длине.
- Сторона da не параллельна стороне bc и не равна ей по длине.
Таким образом, имея такие характеристики, четырехугольник abcd нельзя считать трапецией.



