Числа - это одна из главных составляющих нашей жизни. Мы используем их для измерения времени, расстояний и многих других величин. Они помогают нам понять и описать мир вокруг нас. Числа, которые мы используем каждый день, могут быть как четными, так и нечетными. Но почему это так?
Разделение чисел на четные и нечетные связано с их делением на 2. Если число делится на 2 без остатка, то оно считается четным. Например, числа 2, 4, 6 и 8 являются четными, так как они делятся на 2 без остатка. С другой стороны, если число не делится на 2 без остатка, оно считается нечетным. Например, числа 1, 3, 5 и 7 являются нечетными, так как они не делятся на 2 без остатка.
Четность и нечетность чисел имеют множество свойств и особенностей. Например, если мы просуммируем два четных числа или два нечетных числа, то результат всегда будет четным. Однако, если мы просуммируем четное и нечетное число, то результат будет нечетным. Это интересное свойство чисел помогает нам решать различные задачи и применять их в практической жизни.
Что такое числа?
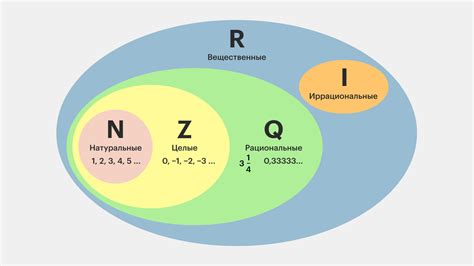
Числа можно классифицировать по различным критериям, включая их тип, свойства и структуру. Одним из основных свойств чисел является их четность. Четные числа делятся нацело на 2, отличаются от нечетных чисел на 1. Нечетные числа не делятся нацело на 2, имеют остаток 1 при делении на 2.
Четность и нечетность чисел обусловлены их внутренней структурой и свойствами. Например, каждое четное число можно представить в виде удвоенного другого числа, в то время как нечетные числа нельзя таким образом представить.
Числа играют важную роль в нашей повседневной жизни. Они используются для измерения времени, количества денег, расстояния и многих других величин. Независимо от того, является ли число четным или нечетным, оно представляет определенное значение и имеет свое место в математике и в реальном мире.
Виды чисел
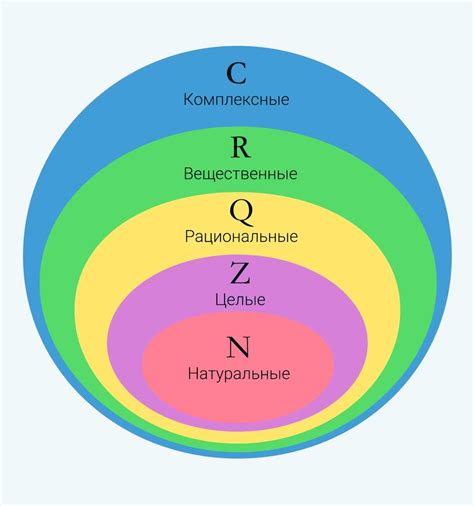
В математике числа могут быть разделены на несколько видов, в том числе четные и нечетные числа.
Четные числа – это числа, которые делятся на 2 без остатка. Например, 2, 4, 6, 8 и так далее. Если представить четное число в виде n = 2k, где k - некоторое целое число, то получим, что оно является четным.
Нечетные числа – это числа, которые не делятся на 2 без остатка. Например, 1, 3, 5, 7 и так далее. Если представить нечетное число в виде n = 2k + 1, где k - некоторое целое число, то получим, что оно является нечетным.
С точки зрения алгебры, четные числа могут быть записаны в виде 2n, где n - целое число, а нечетные числа - в виде 2n + 1, где n - также целое число.
Существует еще один важный вид чисел - нуль. Ноль не является ни четным, ни нечетным числом, так как не имеет остатка от деления на 2. Он играет особую роль в математике и используется в различных операциях.
Четные числа

У четных чисел есть некоторые интересные свойства:
1. Двойка делится на все четные числа
Так как четные числа определяются как числа, кратные 2, то может показаться кажется очевидным, что двойка делится на все четные числа. Например, число 4 делится на 2 без остатка, и мы можем записать это как 4 = 2 * 2.
2. Перемножение четных чисел дает четное число
Если умножить два четных числа, результатом также будет четное число. Например, 2 * 4 = 8, где все числа являются четными. Это свойство можно выразить как (2n) * (2m) = 4nm = 2(2nm), где n и m - целые числа.
3. Четные числа являются симметричными
Многие четные числа имеют зеркальную симметрию. Например, число 6 можно представить как два равных половинчатых отрезка 3 + 3. То есть, если мы разделим четное число пополам, мы получим два одинаковых числа.
Важно отметить, что все целые числа могут быть классифицированы как четные или нечетные. Числа, не являющиеся четными, называются нечетными числами. Различие между четными и нечетными числами является важным понятием в математике и имеет различные применения в решении различных задач.
Нечетные числа

Нечетные числа можно представить в виде арифметической прогрессии: 1, 3, 5, 7, 9 и так далее. Между каждыми двумя последовательными числами в этой прогрессии всегда имеется разница в 2.
Нечетные числа играют важную роль в математике и естественных науках. Они используются, например, при решении уравнений, вычислении вероятностей и во многих других областях. В программировании нечетные числа могут использоваться для различных операций и проверок условий.
Изучение нечетных чисел помогает лучше понять алгебру и числовые системы. Знание и понимание нечетных чисел может быть полезным при анализе и решении различных проблем, а также повысить общую математическую грамотность.