Когда говорят о простых числах, большинство из нас наверняка вспоминает школьный курс математики, где учитель объяснял, что простыми числами являются только те числа, которые делятся без остатка только на себя и на единицу.
Однако, есть одно число, которое не совпадает с этим определением - число 1. Почему же 1 не считается простым числом? Все дело в том, что простые числа являются фундаментальными строительными блоками для всех остальных чисел, а 1 не обладает таким свойством.
Если мы будем считать 1 простым числом, то мы нарушим основные свойства и законы математики. Например, любое число можно представить в виде произведения простых чисел, и такое представление будет единственным. Если бы 1 было простым числом, то единственное представление чисел в виде произведения простых сомножителей нарушилось бы.
История числа 1
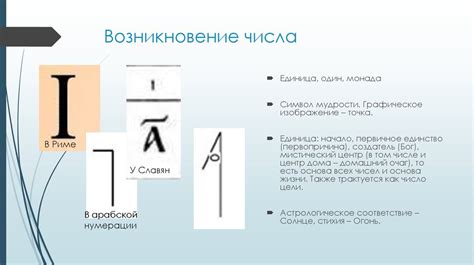
Использование числа 1 в ходе счета было описано множеством древних цивилизаций. Оно являлось основой для развития математических концепций и систем измерения. Именно с числа 1 начинается естественный ряд натуральных чисел.
Символ 1, который мы используем сегодня, происходит от латинской буквы "I". Этот символ появился в Древнем Риме и был частью римской системы счета. Позже, в рамках арабской системы счета, цифра 1 была представлена формой горизонтальной палочки.
Однако, число 1 имеет не только численное значение, но и символическую силу. Оно олицетворяет единство и целостность, а также выражает концепцию первенства и начала. Число 1 используется в различных науках, искусстве и философии для обозначения первичности и фундаментальности.
Хотя число 1 не является простым числом, оно играет ключевую роль в математике и обществе. Его уникальные свойства и символическое значение делают его неотъемлемой частью нашей жизни.
Роль числа 1 в сметрных системах
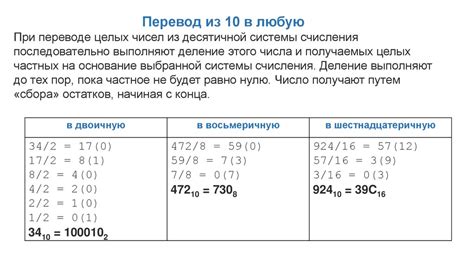
Во-вторых, число 1 является единицей измерения в множестве единиц, которые играют важную роль в наших повседневных расчетах. Например, мы измеряем расстояние в метрах, вес - в килограммах, время - в секундах. В каждой из этих систем единица является относительной, но существенной частью.
Кроме того, число 1 также выполняет важную функцию в логических и алгебраических операциях. Оно является и дополнительным элементом в алгебраических выражениях, и первым шагом при решении уравнений и построении графиков функций. Без числа 1 невозможно провести арифметические операции и осуществлять точные измерения.
Таким образом, число 1 играет важную роль в сметрических системах, будучи отправной точкой и основой для всех вычислений. Без этого числа невозможно представить себе математическую науку и нормальное функционирование нашей бытовой и профессиональной жизни.
Появление понятия "простое число"

Понятие "простое число" возникло в античном мире и было связано с изучением чисел и их свойств. В Древней Греции, где развивались математика и философия, возникла потребность в классификации чисел и выделении специальных групп.
Первым математиком, который занимался изучением простых чисел, считается древнегреческий ученый Евклид, живший около III века до н.э. В его труде "Начала" было введено понятие "простых чисел" и дано их определение.
Евклид определил простые числа как числа, на которые нельзя разделить без остатка, кроме деления на 1 и само число. Таким образом, простые числа представляют собой числа, у которых нет делителей, кроме 1 и самого себя.
Евклид описал свойство простых чисел, которое называется "основная теорема арифметики". Она заключается в том, что каждое натуральное число больше 1 может быть представлено в виде произведения простых чисел, причем это представление единственно.
Таким образом, понятие "простое число" является одним из основных понятий в теории чисел и играет важную роль в математике.
| Примеры простых чисел: |
|---|
| 2 |
| 3 |
| 5 |
| 7 |
| 11 |
| 13 |
| ... |
Характеристики числа 1

Простые числа определяются как натуральные числа, которые имеют только два делителя: 1 и само число. В то время как число 1 имеет только один делитель, оно не удовлетворяет этому определению и, следовательно, не является простым числом.
Хотя число 1 не является простым, оно все же играет важную роль в математике и других областях. Например, оно является единицей в отношении умножения и дает тождественное значение при возведении в степень 0. Кроме того, число 1 играет важную роль в компьютерных науках, где используется в различных алгоритмах и структурах данных.
Уникальные свойства числа 1

Во-первых, число 1 является единицей и используется для обозначения самого маленького числа. Оно является основой для системы счисления и используется во многих математических операциях.
Во-вторых, число 1 является мультипликативной единицей. При умножении любого числа на 1 результат остается неизменным. Это свойство широко используется в математике и физике.
В-третьих, число 1 является нейтральным элементом относительно сложения. При сложении числа 1 с любым числом результат равен второму числу. Это также важное свойство для множества числовых операций.
Таким образом, хотя число 1 не является простым числом, оно обладает множеством уникальных свойств, которые делают его неотъемлемой частью математики и ее приложений.
Теоретические особенности числа 1

Основным критерием для простоты числа является то, что оно имеет ровно два делителя - 1 и само число. Однако число 1 имеет только одного делителя - 1, поэтому оно не удовлетворяет этому критерию и не является простым.
Более того, простота числа также предполагает его большую выразительность, то есть возможность представления его в виде произведения простых множителей. Однако для числа 1 нет такого представления, поскольку оно само является единственным простым множителем.
Таким образом, число 1 отличается особыми теоретическими свойствами, что делает его уникальным среди всех натуральных чисел.
Число 1 в математических операциях

В сложении и вычитании число 1 не вносит изменений. Любое число, прибавленное или вычитаемое из 1, остается неизменным. Например:
- 1 + 5 = 6
- 1 - 3 = -2
Однако, в умножении и делении 1 имеет свои особенности. Например:
- 1 * 5 = 5
- 1 / 3 = 0.3333...
Умножение любого числа на 1 не меняет его значения. Также, деление любого числа на 1 дает то же число. Например:
- 7 * 1 = 7
- 10 / 1 = 10
Кроме того, 1 является единицей в различных системах измерений, таких как длина, масса, время и т.д.
Не смотря на свою уникальность и некоторые особенности, число 1 не является простым числом, так как простые числа определяются как натуральные числа, которые имеют только два делителя: 1 и само число. В случае числа 1, оно имеет только одного делителя - само число 1.
Умножение на 1

Когда мы умножаем любое число на 1, результат остается неизменным: n * 1 = n. Это свойство единицы называется единичным элементом умножения. Оно выполняется для любого числа, за исключением самого числа 1.
Один из способов определить простое число - это число, которое делится только на 1 и само на себя. Но если 1 было бы простым числом, то оно бы не выполняло это свойство, так как 1 делится только на 1. Поэтому 1 не рассматривается в качестве простого числа.
В математике, единица является первым натуральным числом. Она также является интересным числом с точки зрения многих математических теорий и свойств.
Важно помнить, что понятие простых чисел - это чисто математическое определение и не всегда имеет применение в реальном мире.



