Число 100 является одним из наиболее известных чисел в математике, но удивительно, что оно не делится на 3. Эта удивительная особенность 100 вызывает интерес и вопросы у многих людей. В данной статье мы постараемся разобраться в причинах и объяснить этот феномен.
В основе объяснения лежит факт, что число 100 содержит одну единицу и два нуля. При делении числа на 3, результирующая сумма цифр должна быть кратной 3. Однако, сумма цифр числа 100 равна 1, что не является кратным числу 3. Это объясняет, почему 100 не делится на 3 и не дает остатка при делении.
Еще одна причина, по которой 100 не делится на 3, заключается в его десятичной системе счисления. В десятичной системе счисления каждая цифра в числе имеет значение, равное степени числа 10. Однако, число 3 не является делителем числа 10, поэтому результатом деления 100 на 3 не может быть целое число.
Таким образом, мы видим, что несмотря на свою простоту, число 100 обладает удивительными свойствами, включая то, что оно не делится на 3. Это может показаться странным, но в мире математики такие особенности встречаются довольно часто и могут стать предметом изучения и удивления для ученых и любознательных умов.
Причины и объяснения того, почему число 100 не делится на 3

Как известно, чтобы число делилось на 3, необходимо, чтобы сумма его цифр также делилась на 3. В случае числа 100, сумма его цифр равна 1 + 0 + 0 = 1. Очевидно, что число 1 не делится на 3, поэтому число 100 не может делиться на 3.
Другой причиной, по которой число 100 не делится на 3, является то, что оно не удовлетворяет общему правилу делимости на 3. Согласно этому правилу, число делится на 3, если сумма его цифр делится на 3 без остатка. В случае числа 100, сумма его цифр равна 1, и она не делится на 3 без остатка, поэтому число 100 не делится на 3.
Таким образом, число 100 не делится на 3 из-за своей структуры и несоответствия общему правилу делимости на 3. Это свойство числа 100 можно использовать в математических расчетах и аналитических вычислениях, где требуется точное значение, не поддающееся делению на 3.
Математическая особенность

Математическая особенность числа 100 заключается в том, что оно не делится на 3 без остатка. Это связано с тем, что число 100 имеет другое простое разложение, и его разложение на простые множители не включает число 3.
При делении 100 на 3 получается остаток 1. Это означает, что 100 не является кратным числом 3. Кратность числа обозначает, сколько раз одно число содержится в другом без остатка. Если число делится на другое число без остатка, то остаток от деления равен 0.
В случае числа 100, оно делится на числа 2 и 5 без остатка, так как 100 = 2 * 2 * 5 * 5. Но 3 в разложении числа 100 отсутствует.
Математическая особенность числа 100, которое не делится на 3, является всего лишь одним из примеров числовой характеристики. Математика изучает такие особенности чисел и пытается найти регулярности в их появлении и связях.
Остаток от деления
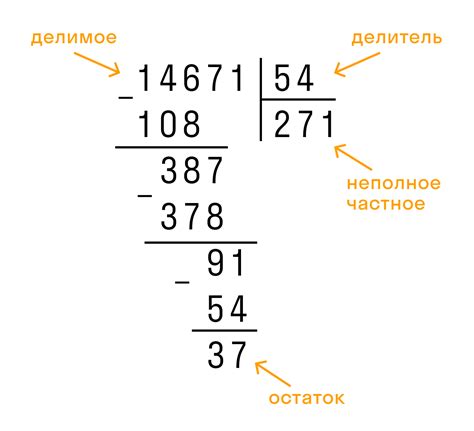
Например, при делении 100 на 3, результатом будет число 33 с остатком 1. То есть 100 = 3 * 33 + 1. В данном случае остаток от деления равен 1.
Если число не делится нацело, то остаток от деления всегда будет меньше делителя. В нашем примере, делитель равен 3 и остаток равен 1.
Остаток от деления часто используется для решения различных задач, например, для определения четности или нечетности числа.
Также остаток от деления имеет своеобразное математическое обозначение - символ "%". То есть, остаток от деления числа a на число b можно записать как a % b.
Правильность расчетов:

Один из основных объяснений тому, что число 100 не делится на 3, заключается в неправильности расчетов. Деление одного числа на другое требует точных математических операций, которые, если выполнены с ошибкой, могут привести к неверному результату.
Например, если мы предположим, что 100 делится на 3, то может возникнуть следующая последовательность расчетов:
100 ÷ 3 = 33.33333333...
Десятичная дробь, которая возникает в этом случае, бесконечно повторяется. Однако, даже если мы округлим результат до целого числа, мы получим:
33
Данное число не является делителем числа 100, поэтому оно не делится на 3.
Таким образом, чтобы правильно определить, делится ли число на 3, необходимо точно выполнять математические расчеты, а также учитывать особенности десятичных дробей и округления результатов.
Важно заметить, что в математике выражение "число делится на N" означает, что есть такое целое число k, для которого выполняется равенство: число = k*N.
Вычисления и округления
Когда мы делаем вычисления, особенно с использованием десятичных дробей, результат может оказаться нецелым числом. Сложные математические операции, такие как деление, могут привести к появлению десятичной дроби в результате. Иногда, результат вычисления может быть очень близким к целому числу, но все же не совпадать с ним.
Округление - это процесс приведения числа к целому числу, ближайшему к нему. В JavaScript, для округления числа, используется функция Math.round(). Например, Math.round(3.14) вернет 3.
Однако, в некоторых случаях, некоторые числа могут быть округлены по-другому. Например, если число заканчивается на .5, оно будет округлено вверх. Например, Math.round(3.5) вернет 4. Это называется "округление половин вверх".
Также, в некоторых случаях, округление может зависеть от контекста. Например, в десятичной системе счисления число 3.15 округляется до 3, а число 3.25 округляется до 3. В двоичной системе счисления, число 3.15 может быть представлено как 3.0010011001... (бесконечное количество двоичных разрядов после запятой), и будет округлено до ближайшего двоичного числа, которое состоит из конечного количества разрядов. В данном случае, это будет число 3.01 (двоичное представление числа 3).
Таким образом, вычисления и округления могут привести к тому, что число, сложенное или умноженное на 3, не будет делиться на 3 без остатка.