Одной из важнейших тем в начальной школе является изучение дробей. Однако, есть ситуации, когда знания по этой теме кажутся совершенно бессмысленными. Восьмой класс – это период, когда ученики сталкиваются с новыми математическими концепциями и начинают задавать себе вопрос: "Зачем мне нужны дроби?".
На самом деле, дроби имеют огромное значение в ряде практических задач и реальных ситуаций. Они помогают решать задачи, связанные с долями, спортивными рекордами, долями вещества и многочисленными другими ситуациями в повседневной жизни.
Однако, для большинства учеников эта математическая тема остаётся абстрактной и трудной для понимания. Возникает вопрос – как показать ученикам, что дроби имеют реальное значение и используются даже в практических ситуациях? Для этого требуется хорошо разработанная программа обучения, включающая в себя интересные примеры, которые помогут ученикам увидеть практическую значимость дробей.
Основные понятия дробей

Числитель - это число, которое находится над чертой дроби. Он указывает, сколько малых частей целого числа мы рассматриваем.
Знаменатель - это число, которое находится под чертой дроби. Он указывает на количество равных частей, на которые целое число разделено.
Дробь в явной форме - это дробь, в которой числитель меньше знаменателя.
Например: дробь 3/4 представляет собой число, которое получается при делении целого числа на 4 равные части и берется 3 из них.
Сравнение дробей - это процесс определения, какая из двух дробей больше или меньше.
Простая дробь - это дробь, у которой числитель и знаменатель не имеют общих делителей, кроме 1.
Смешанная дробь - это дробь, которая состоит из целой части и обыкновенной дроби.
Например: 1 1/2 - это смешанная дробь, которая обозначает 1 целую часть и 1/2 доли числа.
Освоив основные понятия дробей, можно успешно выполнять задания по этой теме и применять их в решении математических задач.
Значение дроби как числа

Дробь представляет собой математическую конструкцию, которая выражает отношение двух чисел. Как числовое значение дробь указывает, сколько раз одно число содержится в другом. Например, дробь 1/2 обозначает, что одно число содержится в другом два раза.
Когда работаем с дробями, мы можем использовать их для различных математических операций, таких как сложение, вычитание, умножение и деление. Дроби также могут быть преобразованы в десятичные дроби, что позволяет сравнивать их и выполнять дополнительные вычисления.
Важно понимать, что значение дроби может быть как положительным, так и отрицательным, в зависимости от знака числителя и знаменателя. Например, дробь -3/4 указывает на отрицательное значение, так как числитель отрицателен.
Значение дроби может быть представлено в различных форматах, включая несократимую дробь, смешанную дробь и десятичную дробь. Каждый из этих форматов имеет свои особенности и может быть использован в зависимости от конкретной задачи.
В школьной программе 8 класса изучение дробей является важной частью курса математики. В процессе изучения дробей учащиеся узнают, как выполнять операции с ними и как использовать их в реальных ситуациях. Понимание значения дробей позволяет ученикам решать задачи, связанные с долями, долями целых чисел и другими применениями.
Определение натуральной дроби

Натуральные дроби можно представить в виде десятичной дроби с конечным или повторяющимся десятичными разложением, однако натуральные дроби могут быть представлены и в виде обыкновенной дроби, где числитель и знаменатель указываются явно.
Примеры натуральных дробей:
- 1/2
- 2/3
- 3/4
- 5/6
Натуральные дроби широко используются в математике и естественных науках для представления долей, отношений и пропорций. Они играют важную роль в решении задач и вычислениях, а также помогают понять физические и геометрические явления.
Избыточные дроби и их применение

Определение избыточной дроби может быть сформулировано следующим образом: это рациональное число, для которого выполняется неравенство m/n > (m-1)/(n-1), где m и n - целые числа и n > 1.
Одним из применений избыточных дробей являются приближения вещественных чисел. Например, число Пи (π) можно приблизить с помощью избыточных дробей. Чем больше знаменатель дроби, тем точнее будет приближение.
Еще одним интересным применением избыточных дробей является кодирование и сжатие информации. В определенных случаях использование избыточных дробей может позволить сократить количество бит, необходимых для представления данных.
Изучение избыточных дробей может быть полезным и интересным для учащихся 8 класса, поскольку оно поможет им расширить свои знания в области математики и увидеть необычные приложения этих чисел в реальном мире.
Арифметические действия с дробями
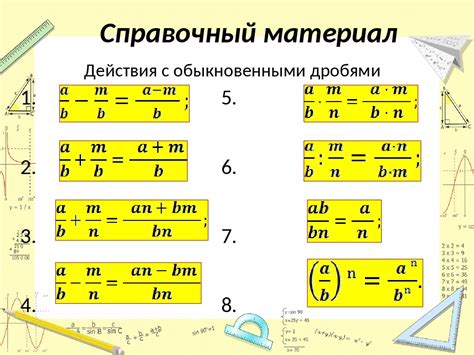
Основные арифметические действия с дробями включают:
| Действие | Обозначение | Пример |
|---|---|---|
| Сложение | + | a/b + c/d = (ad + bc)/bd |
| Вычитание | - | a/b - c/d = (ad - bc)/bd |
| Умножение | * | a/b * c/d = ac/bd |
| Деление | / | a/b / c/d = ad/bc |
При выполнении арифметических действий с дробями, важно учесть общий знаменатель и не забыть упростить полученную дробь до несократимого вида.
Десятичные дроби и их приложение

Десятичные дроби представляют собой числа, которые содержат десятичную точку и цифры после нее. Число перед десятичной точкой называется целой частью, а цифры после десятичной точки - дробной частью. Например, в числе 3.14, "3" - целая часть, а "14" - дробная часть.
Важно помнить, что десятичные дроби обычно записываются с помощью десятичной системы счисления. В этой системе каждая цифра в числе имеет определенную позицию, которая определяет ее вес. Например, в числе 3.14, "3" имеет вес 3 в позиции единиц, а "1" имеет вес 1 в позиции десятых. Таким образом, десятичные дроби позволяют удобно представлять и работать с дробными числами.
Применение десятичных дробей в реальной жизни начинается с момента, когда нам необходимо измерить что-то или представить результаты измерений в виде чисел. Например, мы измеряем длину, вес, объем и другие величины. В результате измерений получаются десятичные дроби, которые позволяют точно и удобно выразить результаты.
| Пример | Область применения |
|---|---|
| 0.5 | Расстояние между двумя точками в километрах |
| 2.75 | Объем жидкости в литрах |
| 4.25 | Цена товара в долларах |
Как видно из примеров, десятичные дроби позволяют точно и удобно представлять различные величины и результаты измерений. Они также используются в финансовых расчетах, научных исследованиях и других областях, где работа с дробными числами является необходимой.
Изучение десятичных дробей в 8 классе играет важную роль в развитии математического мышления у учеников. Оно помогает им лучше понять и применять десятичные дроби в реальной жизни, а также развивает навыки работы с числами и решения математических задач.
Практические примеры на основе дробей

Пример 1: Представим, что у вас есть пицца, разделенная на 8 равных частей. Если вы съели 3 из них, какая доля пиццы осталась?
Чтобы решить этот вопрос, мы можем использовать понятие дробей. Если каждая часть пиццы представляет собой одну восьмую (1/8) пиццы, то остаток будет составлять 5/8 пиццы.
Пример 2: Представим, что у вас есть задача, в которой каждый день вы работаете над проектом 3 часа из 8, которые вам доступны. Сколько времени остается до завершения проекта?
Так как каждый день вы тратите 3/8 времени на работу, остается 5/8 времени до завершения проекта.
Пример 3: Представим, что вы решили сделать ремонт в комнате, и вам нужно купить краску. Краска продается в банках объемом 1/4 литра. Если вам нужно покрасить стену, занимающую 3/4 квадратных метра, сколько банок краски вам понадобится?
Чтобы решить эту задачу, мы можем просчитать объем краски, необходимый для покраски 1 квадратного метра (1/4 литра) и умножить его на площадь стены (3/4 квадратных метра). Таким образом, нам потребуется 3/16 литра краски, что эквивалентно 3/4 банки краски.
Для лучшего понимания математических операций с дробями рекомендуется практиковаться на подобных примерах и задачах. Это поможет закрепить знания и умение применять их на практике.