Перпендикулярные прямые - это две прямые, которые пересекают друг друга под прямым углом. Такие прямые имеют особую геометрическую связь и важны в различных областях науки и ежедневной жизни.
Понимание того, почему две прямые перпендикулярные к третьей, необходимо для решения множества задач и построения точных измерений. Знание основных свойств перпендикулярных прямых помогает понять многое о форме и структуре объектов.
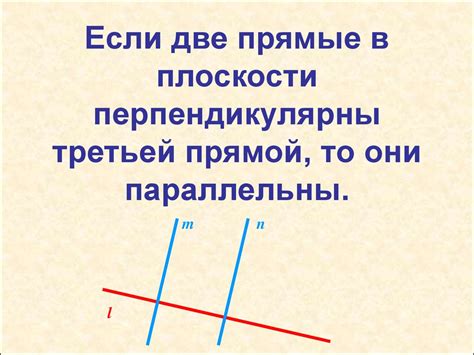
Одно из фундаментальных свойств перпендикуляра: если две прямые перпендикулярные к одной третьей прямой, то они также оказываются перпендикулярными друг другу. И наоборот, если две прямые пересекают одну третью прямую под прямым углом, то они будут перпендикулярны друг другу.
Важность понимания перпендикулярных прямых
Перпендикулярные прямые играют ключевую роль во множестве геометрических задач и конструкций. Знание того, что две прямые перпендикулярны к третьей, позволяет нам применять различные строительные методы, а также решать задачи на построение перпендикуляра к данной прямой.
Треугольники, прямоугольные прямоугольники и параллелограммы, основанные на перпендикулярных прямых, широко используются в архитектуре и строительстве. Например, перпендикулярные прямые помогают строить предметы и сооружения с определенными геометрическими параметрами, такими как вертикальность и горизонтальность.
В области технического рисования и инженерных наук, перпендикулярные прямые используются для создания точных и симметричных чертежей. Они также помогают в измерениях и геометрическом моделировании.
| Примеры использования перпендикулярных прямых |
|---|
| 1. Построение перпендикуляра к заданной прямой в геометрии. |
| 2. Создание прямоугольного треугольника, используя перпендикулярную прямую. |
| 3. Построение перпендикулярного биссектрисы в треугольнике. |
| 4. Конструирование прямоугольника с помощью перпендикулярных прямых. |
Понимание перпендикулярных прямых позволяет нам решать задачи, связанные с построением, измерениями и геометрическими преобразованиями. Это навык, необходимый не только для математиков, но и для различных профессионалов в области архитектуры, инженерии и дизайна. Поэтому, важно уделять достаточное внимание изучению и пониманию понятия перпендикулярных прямых.
Зачем нужно знать про перпендикулярные прямые в геометрии
Знание перпендикулярных прямых позволяет нам построить перпендикуляр к заданной прямой, используя только циркуль и линейку. Это важный навык, который может быть применен не только в математике, но и в других областях, таких как архитектура и инженерное дело. Например, при строительстве зданий и дорог часто необходимо строить отрезки перпендикулярно друг другу.
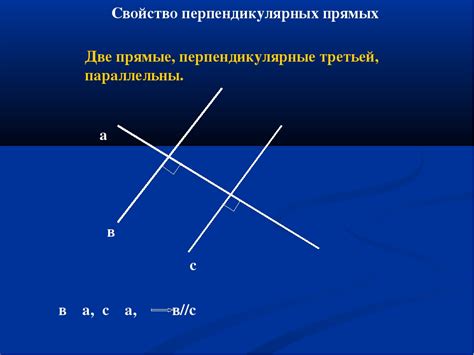
Знание перпендикулярных прямых также помогает в понимании свойств углов. Если две прямые перпендикулярны к одной и той же прямой, то они параллельны друг другу. Это открывает новые возможности для изучения и классификации углов, таких как прямой угол, острый угол и тупой угол.
Кроме того, перпендикулярные прямые играют важную роль в решении задач на построение треугольников и других фигур. Зная, что перпендикулярные прямые являются основой для построения прямоугольников и квадратов, мы можем применять эти знания для решения задач на построение фигур различных форм и размеров.
Таким образом, знание о перпендикулярных прямых позволяет нам лучше понять геометрические свойства и взаимосвязи между объектами. Этот навык может быть полезен не только в школе, но и в повседневной жизни, помогая разрабатывать решения и применять геометрические принципы в практических задачах.
Прямая перпендикулярная к плоскости и к другой прямой
Когда говорят о перпендикулярных линиях, часто вспоминается случай, когда две прямые пересекаются и образуют угол в 90 градусов. Однако, существуют другие случаи, когда прямая может быть перпендикулярна плоскости или другой прямой.
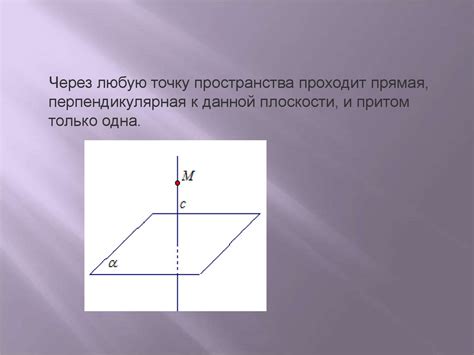
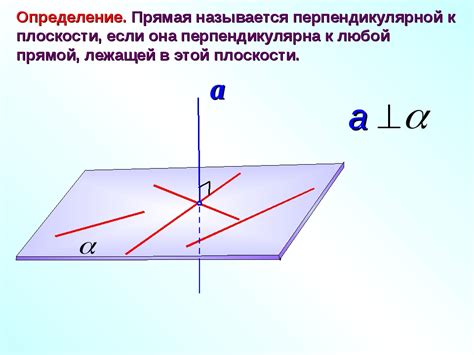
Прямая перпендикулярная к плоскости может быть определена как прямая, которая проходит через точку на плоскости и перпендикулярна всем прямым линиям, лежащим в этой плоскости. Такая прямая будет образовывать угол в 90 градусов со всеми линиями, лежащими в плоскости.
Примером такой прямой может служить вектор нормали к плоскости. Вектор нормали перпендикулярен к плоскости и указывает в направлении, перпендикулярном плоскости. Этот вектор может быть использован для определения угла между линиями или для нахождения расстояния от точек до плоскости.
Если искать прямую, перпендикулярную другой прямой, то такая прямая будет проходить через данную прямую и образовывать с ней угол в 90 градусов. Например, прямая, проходящая через середину отрезка и образующая угол в 90 градусов с этим отрезком, будет перпендикулярна данному отрезку.
Оба этих случая подчеркивают важность понимания понятия перпендикулярности в геометрии и его применения при решении задач. Перпендикулярные линии играют важную роль в построении геометрических фигур, нахождении расстояний и измерении углов.
Объяснение понятия перпендикулярных прямых в трехмерном пространстве
Для наглядности рассмотрим таблицу, в которой указаны координаты трех прямых в трехмерном пространстве:
| Прямая | Уравнение | Направляющий вектор |
|---|---|---|
| Прямая 1 | x = 2 + t | < 1, 0, 0 > |
| Прямая 2 | y = 1 + 2t | < 0, 2, 0 > |
| Прямая 3 | z = 3 + 3t | < 0, 0, 3 > |
Из таблицы видно, что координатные плоскости, по которым расположены эти прямые, пересекаются в точке с координатами (2, 1, 3). Каждая из прямых параллельна одной из осей координат, поэтому они могут быть взаимно перпендикулярны только к оси, которой они параллельны.
Таким образом, в трехмерном пространстве две прямые могут быть перпендикулярны третьей, если они взаимно перпендикулярны этой третьей прямой и параллельны двум осям координат.
Примеры практического применения перпендикулярных прямых
Перпендикулярные прямые находят широкое применение в различных областях, включая геометрию, строительство, архитектуру, графику и дизайн. Вот несколько примеров практического использования перпендикулярных прямых:
1. Построение прямых углов: Перпендикулярные прямые используются для создания прямых углов. Например, в строительстве перпендикулярные линии помогают определить точное положение стен, окон, дверей и других элементов зданий.
2. Измерение и разметка: Перпендикулярные прямые могут быть использованы для измерения и разметки. Например, при строительстве дороги перпендикулярные линии могут быть использованы для разметки полос движения и обозначения перекрестков.
3. Конструирование параллельных линий: Перпендикулярные прямые могут быть использованы для построения параллельных линий. Например, в архитектуре перпендикулярные линии могут использоваться для создания перспективы и пропорций зданий.
4. Решение геометрических задач: Перпендикулярные прямые используются для решения различных задач в геометрии. Например, они могут помочь найти высоту треугольника или определить перпендикулярную биссектрису отрезка.
5. Графический дизайн: Перпендикулярные прямые могут быть использованы для создания геометрического баланса в графическом дизайне. Они могут быть использованы для выравнивания элементов, создания сетки или задания определенной композиции.
6. Геодезия и картография: В геодезии и картографии перпендикулярные прямые помогают определить координаты точек на поверхности Земли и построить карты с высокой точностью.
| Область применения | Примеры |
|---|---|
| Строительство | Определение расположения элементов зданий |
| Архитектура | Создание перспективы и пропорций зданий |
| Дизайн | Выравнивание элементов и создание сетки |
| Геометрия | Решение геометрических задач |
| Геодезия и картография | Определение координат точек и построение карт |