Движение по окружности является одним из самых интересных и изучаемых объектов в физике и математике. Оно привлекает внимание своей гармоничностью и простотой. Равномерное движение по окружности, как частный случай, является особенно интересным, поскольку в этом случае скорость и направление движения остаются неизменными на протяжении всего пути.
Равномерное движение по окружности отличается от произвольного движения тем, что оно характеризуется постоянной угловой скоростью. Это значит, что за равные промежутки времени тело преодолевает одинаковые углы. Однако, несмотря на то, что скорость движения не меняется, а центростремительное ускорение остается постоянным, значит, движение равномерное.
Такое движение можно наблюдать во многих явлениях окружающей нас реальности. Например, планеты движутся по орбитам вокруг Солнца, а спутники - вокруг Земли. Равномерное движение по окружности также является основой работы многих механизмов и технических устройств.
Значение термина "равномерное движение"
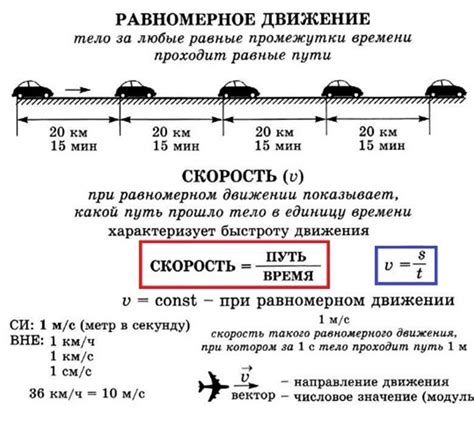
В случае равномерного движения скорость тела остается постоянной на всем пути. Это означает, что тело проходит одинаковые расстояния за одинаковые промежутки времени. Например, если автомобиль едет по кругу с постоянной скоростью 60 км/ч, то он проходит 60 километров за каждый час движения.
Если тело движется с постоянной скоростью и меняет направление движения, такое движение также считается равномерным. Например, если человек ходит по окружности, круговая дуга которой делится на равные участки за одинаковое время, его движение будет считаться равномерным, несмотря на изменение направления движения.
Равномерное движение является одним из базовых понятий в физике и широко используется для упрощения математических моделей и расчетов. Важно помнить, что равномерное движение - это идеализированная модель, которая редко встречается в реальной жизни, так как большинство объектов движется с изменяющейся скоростью и в разных направлениях.
Особенности движения по окружности
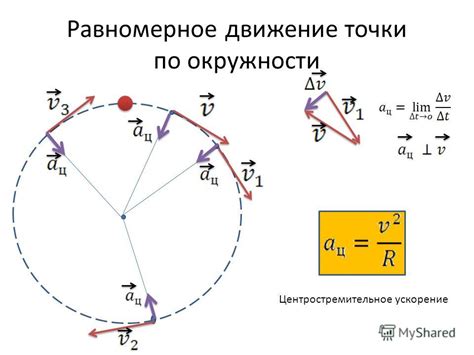
Движение по окружности отличается от других типов движений тем, что оно характеризуется постоянной скоростью и изменением направления движения. В результате этого, движение по окружности часто называют равномерным.
Равномерное движение по окружности имеет ряд особенностей. Во-первых, точка движется по окружности с постоянной линейной скоростью, что означает, что она проходит одинаковые участки пути за одинаковые промежутки времени.
Во-вторых, радиус вектор точки всегда перпендикулярен к касательной к окружности в данной точке. Это означает, что сила, действующая на точку, всегда направлена к центру окружности и называется центростремительной.
Также, движение по окружности обладает периодичностью, так как точка возвращается в исходное положение после каждого оборота по окружности.
Особенности равномерного движения по окружности имеют важное значение в физике, механике и других науках, где изучаются законы и свойства движения. Понимание этих особенностей позволяет решать задачи и выявлять закономерности в движении тел.
Основные параметры равномерного движения
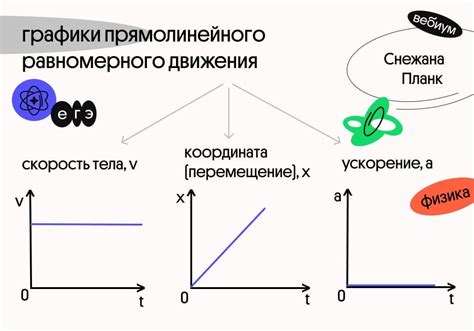
Равномерное движение по окружности характеризуется определенными параметрами, которые позволяют его описать исчерпывающим образом.
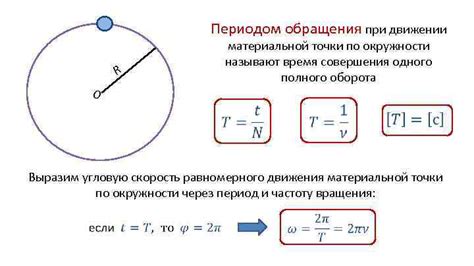
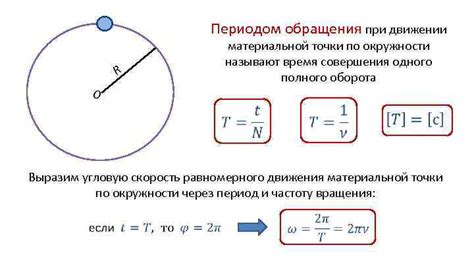
Период (T): это временной интервал, за который тело совершает полный оборот по окружности. Он измеряется в секундах и представляет собой время, необходимое для прохождения точкой одного полного круга.
Частота (f): это величина, обратная периоду. Частота показывает количество полных оборотов, совершаемых телом за единицу времени. Измеряется в герцах (Гц).
Угловая скорость (ω): это векторная величина, которая показывает, как быстро меняется угол, составленный радиусом и вектором скорости. Измеряется в радианах в секунду (рад/с).
Центростремительное ускорение (a): это ускорение, направленное по радиусу и вызывающее изменение направления движения. Модуль центростремительного ускорения можно вычислить по формуле a = ω^2 * r, где r - радиус окружности.
Зная эти параметры, можно тщательно изучать и анализировать движение по окружности и его особенности.
Физические основы равномерного движения
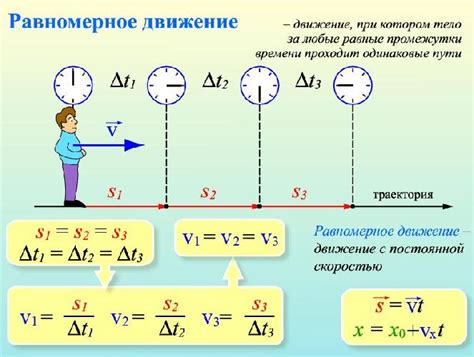
Для описания равномерного движения используется понятие скорости – величина, которая характеризует изменение положения тела за единицу времени. В случае равномерного движения, скорость остается постоянной и не изменяется на протяжении всего пути.
Скорость равномерного движения можно выразить формулой:
v = s/t
где v – скорость равномерного движения, s – пройденное расстояние, t – время, за которое пройдено это расстояние.
Таким образом, равномерное движение является важной физической концепцией, которая позволяет описывать и анализировать движение тела. Оно находит применение в различных науках и технологиях, включая физику, механику и инженерию.
Связь равномерного движения и окружности
Окружность - это геометрическая фигура, состоящая из всех точек, которые находятся на одинаковом расстоянии от центра. Вокруг окружности можно провести множество равномерных движений. Например, если объект движется по окружности с постоянной скоростью, то это движение будет являться равномерным.
При равномерном движении по окружности, каждая точка объекта одинаково удалена от центра окружности. Это означает, что объект описывает равные углы в процессе движения. Благодаря этому, объект совершает равномерное движение по окружности.
Связь между равномерным движением и окружностью заключается в том, что окружность предоставляет возможность для совершения равномерного движения. Окружность является идеальным примером для наглядного представления равномерного движения, так как каждая точка на окружности при движении с постоянной скоростью описывает один и тот же угол.
 |
| Рисунок 1. Равномерное движение по окружности |
Важность равномерного движения по окружности
Одним из ключевых преимуществ равномерного движения по окружности является возможность точно вычислить различные параметры движения, такие как скорость, ускорение, время и расстояние. Это позволяет ученым и инженерам разрабатывать различные механизмы и системы, такие как автомобили, самолеты и спутники, с учетом особенностей равномерного движения.
Кроме того, равномерное движение по окружности имеет прямое отношение к задачам геометрии и тригонометрии. Оно помогает в изучении основ теории вероятностей, статистики и многих других дисциплин.
Не менее важным является то, что равномерное движение по окружности является идеализированным случаем реальных движений. Многие физические системы, такие как электрооборудование, механизмы и устройства, стремятся к равномерному движению, чтобы обеспечить более точное и стабильное функционирование.
В целом, понимание равномерного движения по окружности является необходимым для практического применения физических и математических знаний в нашей жизни. Оно позволяет нам лучше понимать мир вокруг нас и разрабатывать новые технологии и решения для повышения комфорта и безопасности.