Факториал – это одна из базовых математических операций, которая является ключевой для множества математических и научных рассуждений. Понимание того, что факториал всегда положителен, является важным аспектом в области математики. Так как факториал числа определен как произведение всех положительных целых чисел, меньших или равных данному числу, он всегда будет положительным.
Положительность факториала объясняется следующим образом: при вычислении факториала мы множим все положительные целые числа, меньшие или равные данному числу. Даже если исходное число является отрицательным, в процессе вычисления мы будем перемножать только положительные числа, тем самым гарантируя положительность результата. Например, факториал отрицательного числа будет равен факториалу положительного числа с тем же абсолютным значением.
Важно отметить, что факториал является формальной операцией, определенной только для целых чисел. Он не определен для дробей, действительных чисел или комплексных чисел. Также следует помнить, что значения факториала быстро растут с увеличением исходного числа, поэтому для больших чисел факториал может быть огромным.
Факториал: что это и как он вычисляется
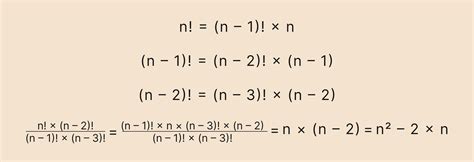
Например, факториал числа 5 вычисляется следующим образом: 5! = 5 * 4 * 3 * 2 * 1 = 120.
Вычисление факториала можно представить с помощью рекурсии или цикла. При использовании рекурсии функция факториала вызывает сама себя, пока не достигнет базового случая, когда аргумент становится равным 1. При использовании цикла факториал вычисляется с помощью итераций от 1 до n, где каждая итерация умножает текущее значение на предыдущее.
Важно отметить, что факториал всегда положителен, так как он является произведением положительных чисел. Ноль и отрицательные числа не имеют факториала, поскольку операция факториала определена только для положительных целых чисел.
Факториал как математическое понятие

Например, факториал числа 5 вычисляется как 5! = 5 * 4 * 3 * 2 * 1 = 120.
Главная причина, по которой факториал всегда положительный, заключается в его определении. Операция факториала определена только для неотрицательных целых чисел. При попытке вычислить факториал отрицательного числа или дробного числа, получается несмысловое выражение.
Еще одно объяснение положительности факториала связано с его геометрическим представлением. Факториал можно интерпретировать как число способов перестановки элементов в последовательности. Например, факториал 5 можно представить в виде 5! = 5 * 4 * 3 * 2 * 1 = 120. Это означает, что существует 120 различных способов переставить пять различных элементов.
Таким образом, факториал всегда положительный, поскольку его определение и геометрическая интерпретация ограничены неотрицательными целыми числами.
Почему факториал всегда положительный

Важно отметить, что факториал всегда положительный независимо от значения исходного числа. Это связано с особенностями математической операции умножения.
Когда мы умножаем два числа, результатом является их произведение. Умножение двух положительных чисел дает положительный результат. Также, умножение одного положительного числа на любое количество других положительных чисел также дает положительный результат.
Факториал числа – это умножение всех натуральных чисел от 1 до данного числа. В этом умножении участвует множество положительных чисел, что гарантирует положительный результат.
Например, рассмотрим вычисление факториала отрицательного числа. Факториал числа -5 равен -5! = -5 * -4 * -3 * -2 * -1 = -120. Здесь видно, что все отрицательные числа умножаются друг на друга, и результат будет отрицательным.
Таким образом, факториал всегда положительный, потому что умножение положительных чисел дает положительный результат, и факториал числа представляет собой произведение всех натуральных чисел, т.е. положительных чисел от 1 до данной величины.
Причины, по которым факториал всегда имеет положительное значение
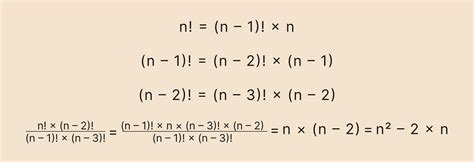
Факториал числа n обозначается символом n!, и представляет собой произведение всех натуральных чисел от 1 до n.
Одной из главных причин, по которым факториал всегда имеет положительное значение, является определение его как произведения чисел. Натуральные числа, входящие в это произведение, всегда положительны, поскольку это числа, которые больше нуля и не являются дробными или отрицательными.
Кроме того, для вычисления факториала используется математическая операция умножения, которая сохраняет знак чисел. Поэтому даже если среди натуральных чисел, входящих в произведение, есть отрицательные числа, результат умножения будет положительным.
Еще одной причиной является то, что факториал часто используется в комбинаторике и теории вероятности, где он используется для подсчета числа комбинаций или перестановок. В этих областях, при подсчете числа комбинаций или перестановок, факториал всегда имеет положительное значение.
Таким образом, причины, по которым факториал всегда имеет положительное значение, связаны с определением факториала как произведения натуральных чисел, свойством умножения сохранять знак чисел и его использованием в комбинаторике и теории вероятности.
Объяснение механизма вычисления факториала
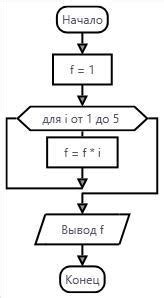
Механизм вычисления факториала состоит в выполнении последовательного умножения всех чисел от 1 до заданного числа n. Начиная с единицы, каждое число последовательно умножается на предыдущее число, пока не достигнет заданного числа n. Таким образом, вычисление факториала происходит по следующей формуле:
n! = 1 * 2 * 3 * ... * (n-1) * n
Например, для вычисления факториала числа 5:
5! = 1 * 2 * 3 * 4 * 5 = 120
Также стоит отметить, что факториал всегда положителен, так как представляет собой произведение натуральных чисел, которые не могут быть отрицательными. Даже если задано отрицательное число в качестве аргумента для вычисления факториала, результат будет всегда положительным.