Теорема – это одно из центральных понятий в математике. Она представляет собой математическое утверждение, которое может быть доказано с использованием определенных аксиом или уже доказанных теорем. Формулировка теоремы - это способ записи самого утверждения, который позволяет ему быть высказанным и понятым другими математиками.
Формулировка теоремы является высказыванием, потому что она является конкретным утверждением, которое может быть либо истинным, либо ложным. Очень важно сформулировать теорему таким образом, чтобы она была четкой и не допускала двусмысленности, чтобы быть понятной и доступной другим математикам. Для этого используются специальные математические символы, сокращения и термины.
Когда формулируется теорема, важно указывать все предположения, на основе которых она должна быть доказана. Это позволяет другим математикам проверить доказательство и убедиться в его достоверности. Формулировка теоремы должна быть строго логичной и следовать из предыдущих результатов, чтобы быть полезной и иметь практическое применение в других областях математики и науки в целом.
Важность формулировки в математике
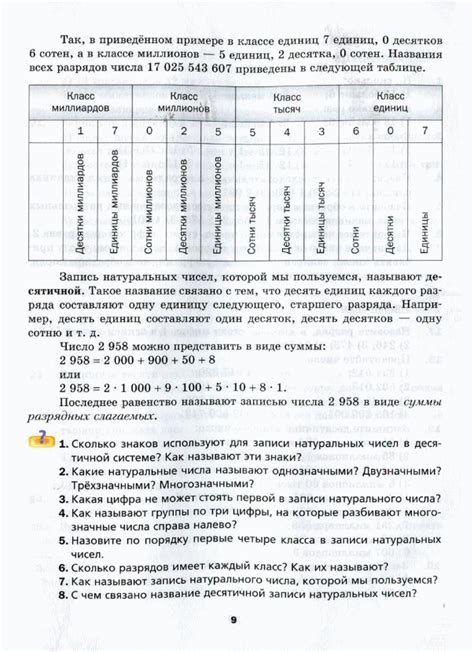
Одна из основных причин, почему формулировка теоремы является высказыванием, заключается в том, что она должна быть верной или ложной. Теорема представляет собой утверждение, которое можно доказать или опровергнуть, и его формулировка должна быть четкой и понятной, чтобы существовала возможность проверить ее истинность.
И наконец, формулировка теоремы должна быть логически связанной и последовательной. Математика базируется на принципах логики, и формулировка теоремы должна быть представлена в таком порядке, чтобы каждое утверждение следовало из предыдущего и приводило к следующему.
Таким образом, формулировка теоремы является высказыванием, потому что она должна быть верной или ложной, четкой и точной, а также логически связанной. Без правильной формулировки теорема теряет свою силу и не может быть удостоверена и проверена.
Особенности формулировки теорем в математике
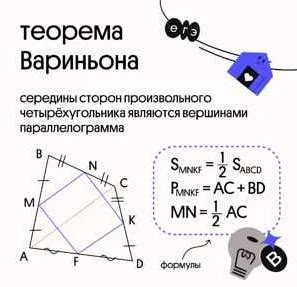
Одна из особенностей формулировок теорем в математике заключается в использовании специальных терминов и символов. Математики используют специальный язык, который позволяет точно и ясно выражать математические концепции. Это помогает избежать разночтений и неоднозначностей в интерпретации теорем.
Еще одной особенностью формулировок теорем в математике является логическая строгость и последовательность. Формулировка теоремы должна быть построена таким образом, чтобы каждый шаг доказательства был логически обоснован и не оставлял сомнений в его верности. Это позволяет ученым и математикам легко проверить и воспроизвести доказательство теоремы.
Важной частью формулировки теоремы является ее условие. Условие теоремы описывает предположения и ограничения, необходимые для применения теоремы. Оно помогает определить область применения и контекст, в котором теорема справедлива. Без правильно сформулированного условия теорема может быть неправильно понята или применена неправильно.
Таким образом, формулировка теорем в математике является важным элементом научного изложения. Она позволяет точно и ясно выражать математические концепции, обеспечивая логическую строгость и ясность в доказательствах. Формулировка теоремы является неотъемлемой частью математического исследования и обеспечивает его надежность и достоверность.
Значение высказывания в формулировке теоремы
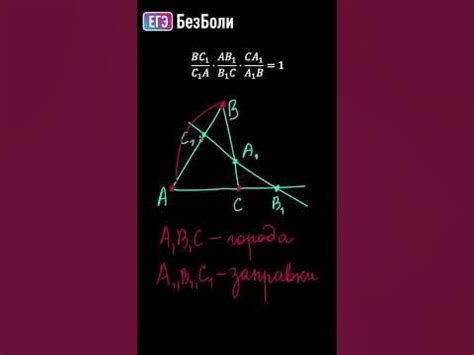
Высказывание в формулировке теоремы играет важную роль в математике. Оно представляет собой утверждение, которое должно быть либо истинным, либо ложным. Формулировка теоремы представляет собой логическое выражение, которое может быть доказано или опровергнуто.
Значение высказывания в формулировке теоремы позволяет установить, является ли данная теорема истинной или ложной. Для этого необходимо провести математическое доказательство, которое основывается на аксиомах, определениях и ранее доказанных теоремах. Если результатом доказательства является истинное высказывание – теорема считается доказанной. В случае, если результатом доказательства является ложное высказывание – теорема опровергается.
Значение высказывания в формулировке теоремы имеет большое значение для развития математики. Доказательство теоремы устанавливает ее истинность и позволяет включить ее в систему математических знаний, что помогает в дальнейших исследованиях и разработке новых математических концепций.
Таким образом, значение высказывания в формулировке теоремы является ключевым элементом в математическом рассуждении и помогает установить истинность или ложность данного утверждения.
Условные и абсолютные высказывания в формулировке теорем

Абсолютное высказывание в формулировке теоремы утверждает, что каждый объект, удовлетворяющий определенным условиям, обладает определенным свойством или является частью определенного класса объектов. Например, теорема Пифагора гласит: "В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов". Это высказывание абсолютно, так как оно говорит о свойстве всех прямоугольных треугольников и их сторон.
Условное высказывание в формулировке теоремы устанавливает, что если выполнены определенные условия, то также выполняется и определенное свойство или отношение между объектами. Например, теорема Ферма гласит: "Нет натуральных чисел x, y, z, для которых x^n + y^n = z^n при n > 2". Это высказывание условное, так как оно говорит о несуществовании таких натуральных чисел при определенном условии - возведении в степень больше двух.
Формулировка теоремы для эффективного восприятия информации

При формулировке теоремы необходимо учитывать следующие принципы:
Ясность Формулировка должна быть ясной и понятной для читателя. Она должна содержать минимум сложных математических терминов и условий, чтобы избежать путаницы и неправильного истолкования. | Краткость Формулировка должна быть лаконичной и содержать минимальное количество слов, чтобы быть доступной для быстрого ознакомления. Излишние детали и повторения следует исключить. |
Точность Формулировка должна быть точной и однозначной, чтобы исключить возможность разных интерпретаций. Каждый термин и понятие должны быть определены четко и правильно. | Адаптированность Формулировка должна быть адаптирована под целевую аудиторию. В зависимости от уровня знаний и математической грамотности читателя, необходимо использовать соответствующий язык и стиль. |
Правильно сформулированная теорема позволяет эффективно и точно передать суть математического доказательства или сформировать основу для дальнейших исследований. Она играет важную роль в науке и познании мира.