Дифференцируемость и непрерывность – это два ключевых понятия в математике, используемые для описания свойств функций. Непрерывность означает, что функция не имеет рывков или разрывов и может быть изображена в виде непрерывной линии на графике. Дифференцируемость, с другой стороны, означает, что функция гладкая и имеет производную в каждой точке своей области определения.
Многие люди ошибочно считают, что если функция непрерывна, она обязательно дифференцируема. Однако это не верно. Непрерывность является необходимым, но не достаточным условием для дифференцируемости функции. Другими словами, непрерывная функция может быть как дифференцируемой, так и не дифференцируемой.
Отсутствие дифференцируемости может быть обусловлено различными факторами, например, функция может иметь разрывы, особые точки или не иметь конечной производной в некоторых точках. Примером такой функции может быть модуль функции или функция Хевисайда.
Таким образом, важно понимать, что дифференцируемость и непрерывность функций представляют собой различные свойства и не следует считать, что отсутствие дифференцируемости автоматически означает нарушение непрерывности.
Математическое определение непрерывности и дифференцируемости

Функция называется непрерывной в точке, если ее значение в этой точке стремится к значению функции в этой точке, приближаясь к нему достаточно близко в любой выбранной окрестности данной точки. Математически это можно записать следующим образом:
- Если функция \( f(x) \) определена на интервале \( (a, b) \) и для любого числа \( c \) из интервала \( (a, b) \) существует предел функции \( f(x) \) в точке \( x = c \), который равен значению функции в этой точке, то функция \( f(x) \) называется непрерывной на интервале \( (a, b) \).
- Если функция \( f(x) \) непрерывна на интервале \( (a, b) \), то она является непрерывной на каждой точке этого интервала.
Дифференцируемость определяет возможность вычисления производной функции в каждой точке ее области определения. Функция называется дифференцируемой в точке, если в этой точке существует ее производная. Математически это можно записать следующим образом:
- Если функция \( f(x) \) определена на интервале \( (a, b) \) и существует предел приращения функции \( \frac{{f(x_0+h)-f(x_0)}}{{h}} \) при \( h ightarrow 0 \), то функция \( f(x) \) называется дифференцируемой в точке \( x_0 \).
Таким образом, непрерывность и дифференцируемость - это важные свойства функций, которые позволяют исследовать их свойства и поведение в различных точках и интервалах. Однако, отсутствие дифференцируемости не всегда следует из непрерывности, поскольку существуют функции, которые непрерывны, но не являются дифференцируемыми в некоторых точках.
Непрерывность функции и ее связь с промежутком изменения
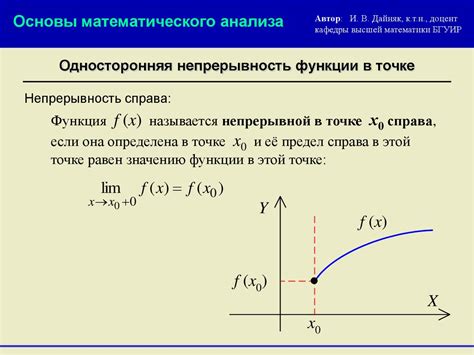
Непрерывность функции тесно связана с промежутком изменения. Промежуток изменения функции – это интервал (отрезок), на котором функция принимает все возможные значения. Если функция непрерывна на данном промежутке, значит она может принимать все значения от минимального до максимального на этом промежутке.
Промежуток изменения функции может быть определен аналитически или графически. Аналитический метод заключается в вычислении значения функции в каждой точке промежутка и изучении полученной последовательности значений. Графический метод заключается в построении графика функции и определении интервала (отрезка) по графику.
Понимание промежутка изменения функции и непрерывности функции имеет большое значение в математическом анализе и его приложениях. Например, в оптимизации функций, непрерывность позволяет использовать методы дифференциального исчисления для нахождения экстремумов функций на заданном промежутке.
| Промежуток изменения | Непрерывность функции |
|---|---|
| [-1, 1] | Функция непрерывна |
| (0, 5) | Функция непрерывна |
| [0, ∞) | Функция непрерывна |
| (-∞, ∞) | Функция непрерывна |
Точки разрыва и их влияние на непрерывность
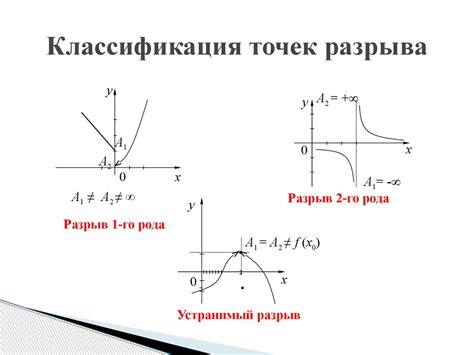
Точка разрыва - это значение, в котором функция либо не определена, либо не может быть непрерывной. Точки разрыва могут возникать по разным причинам, например, из-за отсутствия значений функции в некоторых точках, нарушения условий ее определения или нарушения условий непрерывности.
Одним из примеров точки разрыва является неопределенность вида 0/0 или бесконечность/бесконечность. В таких случаях функция может быть непрерывной, если значение определено в близлежащих точках и можно выполнить ее продолжение. Однако, если значение функции в данной точке не определено или продолжение невозможно, то точка является точкой разрыва.
Точки разрыва могут быть существенными и несущественными. В существенной точке разрыва функция может быть непрерывной, если левый и правый пределы существуют и равны. В случае, если хотя бы один из пределов не существует или они не равны, функция будет иметь существенную точку разрыва и не будет непрерывной.
Несущественная точка разрыва обусловлена особенностями поведения функции в данной точке, например, разрывом первого рода. В этих случаях функция может быть непрерывной вне точки разрыва, но в самой точке значения функции нет или она принимает бесконечное значение. Такие точки разрыва можно устранить, добавив или изменяя значение функции в самой точке, в результате чего функция становится непрерывной на всей области своего определения.
Таким образом, точки разрыва могут существенно влиять на непрерывность функции, определяя ее особенности и характеристики. Из-за точек разрыва функция может перестать быть непрерывной, изменить свое поведение или потерять определенные свойства. Изучение точек разрыва играет важную роль в анализе и исследовании функций, а также позволяет определить их свойства и особенности.
Дифференцируемость функции и ее связь с гладкостью

Дифференцируемость функции в точке означает, что функция имеет в этой точке производную. Производная функции характеризует ее скорость изменения в данной точке и позволяет нам аппроксимировать ее значениетангенсом касательной к графику функции в этой точке.
Однако важно отличать дифференцируемость от непрерывности. Непрерывность функции означает, что ее график не имеет пропусков и разрывов. Непрерывная функция может быть не дифференцируемой в некоторых точках, она может иметь угловые точки, где контур графика совершает резкое изменение, и недостаточно "плавно" меняется.
Иногда функции могут быть гладкими и непрерывными, но не являться дифференцируемыми. Такие функции могут иметь особые точки, где производная не определена из-за различных факторов, таких как разрывы или вертикальные асимптоты. Такие точки называются точками разрыва производной.
- Непрерывная функция может быть дифференцируемой
- Непрерывная функция может не быть дифференцируемой
- Дифференцируемая функция всегда является непрерывной
Таким образом, отсутствие дифференцируемости не следует из непрерывности. Гладкость функции и ее дифференцируемость имеют сложные связи, и чтобы понять их взаимосвязь, необходимо применять математический аппарат исследования функций.
Необходимое условие дифференцируемости

Для того чтобы функция была дифференцируемой в некоторой точке, она должна быть определена в этой точке и иметь конечные односторонние производные. То есть, функция должна быть непрерывной и гладкой в окрестности этой точки.
Простой пример функции, которая является непрерывной, но не дифференцируемой в некоторой точке, - модульная функция:
| x | f(x) = |x| |
|---|---|
| -2 | 2 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
Функция модуля определена для всех действительных чисел и является непрерывной во всех точках, кроме 0. Однако, в точке x=0 у неё происходит "сглаживание", и производная в этой точке не существует. Таким образом, непрерывность не является достаточным условием для дифференцируемости.
Поэтому, чтобы утверждать о дифференцируемости функции, необходимо не только проверить её непрерывность, но также и наличие конечных производных во всех точках окрестности.
Примеры функций, которые непрерывны, но не дифференцируемы
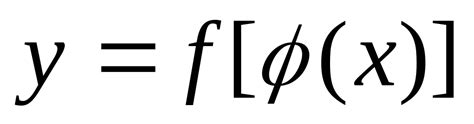
1. Функция Вейерштрасса:
Функция Вейерштрасса, полученная отграфика первой итерации ряда Фурье, является примером непрерывной функции, но не дифференцируемой на всей числовой оси. Она демонстрирует, что непрерывность не гарантирует дифференцируемость, так как она имеет бесконечное число точек разрыва.
2. Функция Тикхонова:
Функция Тикхонова (также известная как "монстр Кантора") является примером функции, которая непрерывна везде, кроме точек из множества Кантора. В этих точках она имеет разрывы и не дифференцируема. Этот пример также демонстрирует, что непрерывность не является достаточным условием для дифференцируемости.
3. Функция Дирихле:
Функция Дирихле (также известная как "функция скрипичная") определена на всей числовой прямой и имеет периодический поток разрывов. Хотя функция Дирихле непрерывна везде, она не является дифференцируемой на большинстве точек своего определения. Это еще один пример функции, которая непрерывна, но не дифференцируема.
4. Функция Абзолютного значения:
Функция абсолютного значения является примером непрерывной функции на всей числовой прямой, но она не дифференцируема в точке 0. Функция имеет "угол разрыва" в этой точке, что приводит к тому, что ее производная не существует в этой точке.
Эти примеры показывают, что непрерывность не следует из дифференцируемости и что существуют функции, которые могут быть непрерывными, но не дифференцируемыми в определенных точках. Отсутствие дифференцируемости не означает, что функция непрерывна или наоборот.