Косинус х является одной из основных тригонометрических функций, которая определяет отношение длины прилежащего катета к гипотенузе прямоугольного треугольника. Эта функция широко применяется в математических и физических расчетах. Часто возникает вопрос: почему значение косинуса х равно значения косинуса х?
Ответ на этот вопрос лежит в особенностях определения косинуса х. Для его вычисления используется ряд Тейлора, который разлагает функцию в бесконечную сумму степеней. При подстановке одного и того же значения аргумента х в обе функции, получается равенство их значений. Это свидетельствует о симметрии косинусной функции относительно оси ординат.
Более формально, косинус х определяется по формуле cos(х) = cos(2π - х), где 2π - х выражает угол, симметричный углу х относительно оси ординат, и cos(2π - х) равен значению косинуса х. Таким образом, функция косинус обладает свойством симметрии, которое объясняет равенство двух косинусов.
Природа косинуса х
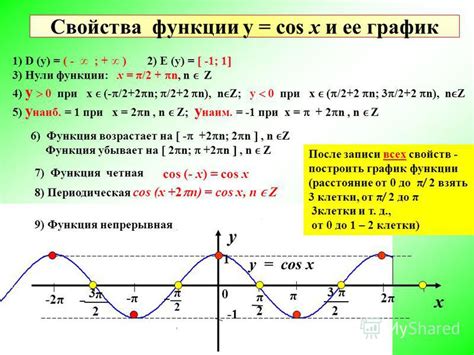
Косинус х (cos(x)) является значением косинуса угла х, где х измеряется в радианах. Значение косинуса х всегда лежит в диапазоне от -1 до 1. Если х представлен в радианах, то косинус х может быть вычислен по формуле:
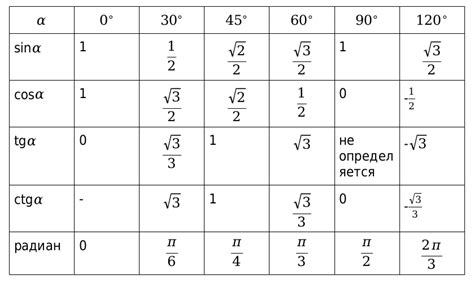
| Угол х (в радианах) | Косинус х |
|---|---|
| 0 | 1 |
| π/6 | 0.866 |
| π/4 | 0.707 |
| π/3 | 0.5 |
| π/2 | 0 |
С помощью таблицы можно заметить, что косинус х обращается в 0 при угле π/2 и достигает максимального значения 1 при угле 0. Другие значения косинуса х можно найти с использованием промежуточных значений в таблице.
Геометрическая интерпретация косинуса
Косинус представляет собой одну из основных тригонометрических функций, которая широко применяется в математике и физике. Геометрическая интерпретация косинуса позволяет понять его сущность и применение.
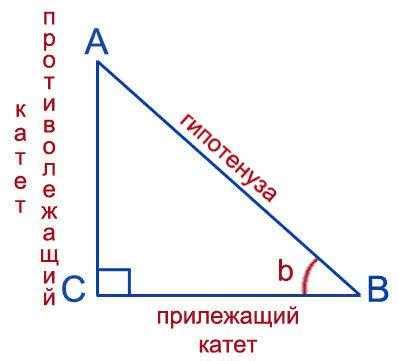
Геометрический смысл косинуса можно объяснить с помощью прямоугольного треугольника. Рассмотрим треугольник ABC, в котором угол BAC равен x.
Косинус угла x определяется как отношение длины прилежащего катета (стороны AB) к гипотенузе (стороне AC) треугольника ABC.
cos(x) = AB/AC
Таким образом, геометрическая интерпретация косинуса заключается в измерении отношения длин двух сторон прямоугольного треугольника.
Пользуясь геометрической интерпретацией косинуса, можно выразить его через другие тригонометрические функции. Например, можно использовать косинус для нахождения синуса угла x:
sin(x) = √(1 - cos^2(x))
Геометрическая интерпретация косинуса является фундаментальным понятием в тригонометрии и открывает двери для дальнейшего изучения связанных математических концепций и приложений в различных областях науки.
Формула вычисления косинуса

cos(x) = adjacent / hypotenuse
Где x – угол, adjacent – длина прилежащего катета, hypotenuse – длина гипотенузы.
Основная особенность косинуса состоит в том, что он может принимать значения в интервале от -1 до 1, где -1 соответствует углу 180 градусов, а 1 – углу 0 градусов.
Косинус используется в различных областях, таких как математика, физика, инженерия и компьютерная графика.
Заметим, что косинус х равен косинусу х в силу того, что косинус является чётной функцией, то есть cos(-x) = cos(x).
Примеры применения косинуса
1. Геометрия: Косинус угла между двумя векторами может использоваться для определения их схожести или параллельности. | 2. Физика: В физике косинус часто используется для определения отношения смежных сторон прямоугольного треугольника, например, при вычислении момента силы. |
3. Телекоммуникации: Косинус может применяться для определения сходства между двумя сигналами или шаблонами и использоваться в алгоритмах распознавания голоса или изображений. | 4. Математика: Косинус является одной из основных тригонометрических функций и находит применение во множестве математических задач, от геометрии до решения уравнений и дифференциальных уравнений. |
Это лишь небольшой набор примеров, где косинус может быть использован. Эта мощная математическая функция имеет много практических применений и продолжает находить применение в различных областях науки и техники.
Следствия из равенства косинуса х косинусу х

1. Косинус является четной функцией
Из равенства косинуса х косинусу х следует, что косинус имеет симметрию относительно оси ординат. Это значит, что для любого x верно равенство cos(x) = cos(-x), где -x - отражение x относительно нуля. Таким образом, значение косинуса не зависит от знака аргумента, что является важным свойством для его применения в различных задачах.
2. Периодичность косинуса
Также из равенства косинуса х косинусу х следует, что косинус является периодической функцией. Равенство cos(x) = cos(x + 2πk), где k - любое целое число, означает, что значение косинуса повторяется через каждые 2π радиан, что соответствует периоду функции. Например, cos(0) = cos(2π) = 1, cos(π) = cos(3π) = -1 и так далее.
3. Тождество косинуса двойного аргумента
Тождество cos(2x) = cos²(x) - sin²(x), которое можно получить из равенства косинуса х косинусу х, является важным инструментом для упрощения выражений и решения различных задач. Оно связывает косинус двойного аргумента с косинусом и синусом исходного аргумента.
Таким образом, равенство косинуса х косинусу х имеет несколько важных следствий, которые находят применение в математике, физике и других науках.



