Квадрат - это геометрическая фигура, которая отличается особыми свойствами. Один из таких факторов - наличие четырех осей симметрии. Это означает, что при повороте квадрата на определенный угол вокруг его центра, фигура остается неизменной. Этот феномен достигается благодаря равным длинам его сторон и углов.
Первая ось симметрии проходит по диагонали квадрата. При повороте фигуры на 180 градусов вокруг этой оси, каждая точка будет симметрична относительно центра квадрата. Это означает, что квадрат остается неизменным после поворота.
Вторая ось симметрии проходит через середины противоположных сторон квадрата. При повороте фигуры на 90, 180 или 270 градусов вокруг этой оси, квадрат остается неизменным. Это свойство квадрата позволяет ему быть симметричным по вертикали или горизонтали.
Третья и четвертая оси симметрии проходят через середины противоположных углов квадрата. При повороте фигуры на 45, 135, 225 или 315 градусов вокруг этих осей, квадрат остается неизменным. Это делает квадрат симметричным относительно диагоналей.
В итоге, квадрат имеет 4 оси симметрии, что делает его особенно уникальным и гармоничным геометрическим объектом.
Что такое оси симметрии?
Квадрат имеет 4 оси симметрии: две вертикальные и две горизонтальные. Вертикальные оси проходят через центры противоположных сторон квадрата, а горизонтальные - через центры противоположных сторон, перпендикулярных вертикальным осям.
Эти оси симметрии позволяют квадрату иметь симметричную форму и являются важными свойствами фигуры. Они используются в математике, дизайне и других областях для создания симметричных композиций и для решения задач, связанных с квадратом.
| Оси симметрии квадрата: | Расположение: | |
|---|---|---|
| Вертикальная ось 1 | Проходит через центры противоположных вертикальных сторон | |
| Вертикальная ось 2 | Проходит через центры противоположных вертикальных сторон | |
| Горизонтальная ось 1 | Проходит через центры противоположных горизонтальных сторон | |
| Горизонтальная ось 2 | Проходит через центры противоположных горизонтальных сторон | |
Основные определения и свойства

| Определение | Квадрат - это четырехугольник, у которого все стороны равны и все углы прямые. |
| Стороны | У квадрата есть четыре стороны, обозначаемые как a, b, c и d. Все они равны между собой. |
| Углы | Квадрат имеет четыре прямых угла, каждый из которых равен 90 градусов. |
| Диагонали | Квадрат имеет две диагонали, которые являются отрезками, соединяющими противоположные вершины. Обозначим их как d1 и d2. |
| Оси симметрии | Квадрат обладает четырьмя осями симметрии, которые проходят через центр квадрата и перпендикулярны друг другу. Они делят квадрат на четыре равные части. |
| Площадь | Площадь квадрата можно найти по формуле: S = a * a, где a - длина стороны квадрата. |
| Периметр | Периметр квадрата можно найти по формуле: P = 4 * a, где a - длина стороны квадрата. |
Что такое квадрат?
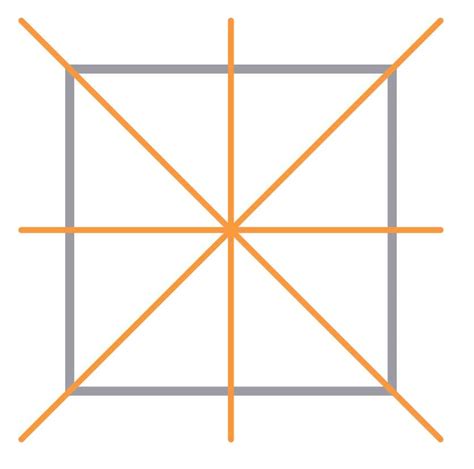
Основные характеристики квадрата:
- Все четыре стороны квадрата равны между собой.
- Углы квадрата равны и составляют 90 градусов.
- Квадрат обладает четырьмя осями симметрии.
- Периметр квадрата вычисляется по формуле: П = 4a, где "a" - длина стороны квадрата.
- Площадь квадрата вычисляется по формуле: S = a^2, где "a" - длина стороны квадрата.
Квадрат широко применяется в различных областях, включая геометрию, архитектуру и искусство. Благодаря своим особым свойствам, квадрат используется в конструкции зданий, создании скверов и парков, а также в дизайне логотипов и графических элементов.
Геометрические характеристики фигуры

- Стороны: Квадрат имеет четыре одинаковые стороны, что делает его основной характеристикой. Каждая сторона перпендикулярна к соседним сторонам.
- Углы: Квадрат также обладает уникальным свойством иметь четыре прямых угла. Все углы в квадрате равны 90 градусам.
- Диагонали: Две диагонали квадрата являются равными и перпендикулярны друг другу. Длина каждой диагонали равна удвоенной длине стороны квадрата.
- Оси симметрии: Квадрат обладает четырьмя осями симметрии. Оси симметрии - это линии, которые делят фигуру на две равные части и совпадают после поворота на определенный угол.
- Периметр: Периметр квадрата может быть вычислен, как сумма всех его сторон. Формула для вычисления периметра квадрата: P = 4s, где P - периметр, s - длина стороны квадрата.
- Площадь: Площадь квадрата может быть вычислена, как произведение длины его стороны на саму себя. Формула для вычисления площади квадрата: A = s^2, где A - площадь, s - длина стороны квадрата.
Эти геометрические характеристики делают квадрат уникальным и полезным в различных областях, таких как архитектура, инженерия, наука и искусство.
Существуют ли оси симметрии у квадрата?
Первая ось симметрии проходит через середину верхней и нижней сторон квадрата, разделяя его на две равные части слева и справа.
Вторая ось симметрии проходит через середину левой и правой сторон, деля квадрат на две равные части сверху и снизу.
Третья ось симметрии проходит через диагональные точки, связывающие верхний левый и нижний правый углы квадрата. Эта ось дает возможность разделить квадрат на две равные диагональные части.
Четвертая ось симметрии проходит через диагональные точки, соединяющие верхний правый и нижний левый углы квадрата. Такая ось симметрии дает разделение квадрата на две равные диагональные части, параллельные третьей оси.
Таким образом, квадрат имеет четыре оси симметрии, каждая из которых позволяет сделать отражение фигуры с сохранением ее формы и размеров.
Обоснование количества осей симметрии
Ось симметрии - это линия, которая делит фигуру на две равные и зеркально отраженные половины. В случае квадрата, его оси симметрии проходят через его центр и соединяют противоположные вершины.
Основным свойством квадрата, которое обусловливает количество его осей симметрии, является равенство всех его сторон и углов. У квадрата все углы равны 90 градусов, а все стороны одинаковой длины.
Из этого следует, что если мы повернем квадрат на угол в 90 градусов вокруг любой из его осей симметрии, он будет выглядеть идентично. То есть, после поворота квадрата, поднятого на грань вниз, он будет совпадать с исходным квадратом.
Таким образом, квадрат имеет четыре оси симметрии, так как он может быть повернут на 90 градусов вокруг каждой из этих осей и сохранять свою форму и положение.
Количество осей симметрии у квадрата является естественным следствием его геометрических свойств. Эти оси делают квадрат идеальной фигурой для создания симметричных и уравновешенных композиций и паттернов.
Какие оси симметрии имеет квадрат?
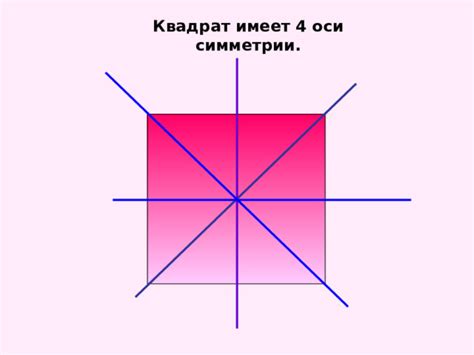
Всего квадрат имеет четыре оси симметрии:
- Вертикальная ось симметрии: проходит через центр квадрата и соединяет середину верхней и нижней сторон.
- Горизонтальная ось симметрии: также проходит через центр квадрата, но соединяет середину левой и правой сторон.
- Оси симметрии, проходящие через углы: проходят через центр квадрата и соединяют противоположные углы. Каждый из четырех углов квадрата является центром для своей оси симметрии.
Имея четыре оси симметрии, квадрат обладает симметрией относительно этих осей, что означает, что его положение остается неизменным при поворотах на углы 90, 180 и 270 градусов. Эта особенность делает квадрат одной из наиболее симметричных фигур в геометрии.
Описание осей симметрии фигуры
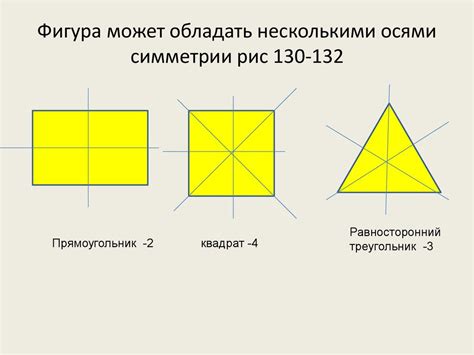
1. Горизонтальная ось симметрии: проходит через центр квадрата и делит его на две равные части, отражая одну часть относительно другой симметрично. Каждая сторона квадрата и ее параллельная сторона будут полностью совпадать после отражения.
2. Вертикальная ось симметрии: также проходит через центр квадрата, но перпендикулярна горизонтальной оси симметрии. Она разделяет фигуру на две симметричные части относительно друг друга.
3. Оси симметрии, проходящие через вершины: для квадрата существует две таких оси, проходящие через противоположные вершины. Каждая такая ось делит фигуру на две симметричные половины, отражая одну часть относительно другой.
4. Диагональная ось симметрии: проходит через центр квадрата и делит его на две зеркальные части. Две грани, параллельные диагонали квадрата, будут совпадать после отражения.
Оси симметрии играют важную роль в геометрии, так как позволяют нам определить симметрию фигуры и использовать её свойства при решении задач.