Лента Мёбиуса - это одно из самых удивительных геометрических объектов, изучение которого всегда вызывает удивление и интерес. Одной из особенностей этой ленты является то, что у нее всего одна сторона. Это означает, что если вы начнете двигаться по этой ленте, то в конечном итоге вернетесь в исходную точку, но сторона, которую вы видели прежде, теперь будет находиться с другой стороны. Это явление может показаться странным и неоднозначным, но у ленты Мёбиуса есть своя геометрическая объяснение.
Лента Мёбиуса получила свое название в честь немецкого математика Августа Фердинанда Мёбиуса, который первым описал и изучал этот объект в 1858 году. Лента Мёбиуса создается путем взятия полоски бумаги, например, и склеивания ее концов таким образом, чтобы одну из сторон полоски можно было повернуть на 180 градусов и соединить с другой стороной полоски. Таким образом, получается искривленная лента с одной стороной.
Для того чтобы понять, почему у ленты Мёбиуса одна сторона, можно провести простой эксперимент. Представьте, что вы находитесь на поверхности такой ленты и начинаете двигаться вдоль ее. Когда вы вернетесь в исходную точку, вы обнаружите, что сторона, которую вы наблюдали до этого момента, теперь находится с другой стороны. Это происходит потому, что лента Мёбиуса имеет только одну грань, которая образуется в результате объединения двух ранее отдельных сторон.
Лента Мёбиуса: почему у нее одна сторона

Понять, почему это так, можно с помощью простого эксперимента. Если взять шарик и намотать на него обычную полосу, то можно легко понять, что она имеет две стороны: внешнюю и внутреннюю. Однако, если намотать ленту Мёбиуса на этот же шарик и провести по ней карандашом, то можно убедиться, что лента образует замкнутую линию без разрывов и внутренних поверхностей.
Разгадка этой загадки кроется в том, что при проведении карандаша по ленте Мёбиуса мы проходим одновременно по обеим ее сторонам. Иначе говоря, каждый полный оборот по ленте Мёбиуса вносит в нашу линию поворот на 360 градусов и приносит карандаш обратно на исходную сторону. Это противоречит нашему привычному представлению о плоскости, которая имеет две стороны на каждую сторону ленты.
Таким образом, лента Мёбиуса является примером геометрического объекта, который нарушает привычные законы плоскости и демонстрирует особенности многомерного пространства.
История открытия

Мёбиус работал с теорией узлов, но однажды, пока он разрезал кольцо, чтобы сделать петлю для своего сына, ему пришла в голову идея повернуть полоску на 180 градусов перед склеиванием. В результате получилась лента Мёбиуса. Непростые свойства этой петли поразили ученого и стали объектами его исследований.
Открытие Мёбиуса стало одним из прорывных моментов в математике, и лента Мёбиуса стала достаточно популярным объектом для изучения не только математиками, но и в физике, химии и других науках. Сегодня лента Мёбиуса является символом бесконечности и вечности, а также используется в различных элементах дизайна и искусства.
Объяснение геометрическими законами

Объяснение этого феномена можно найти в геометрических законах, которые действуют на ленту Мёбиуса. Представьте себе, что вы берете полоску бумаги, склеиваете ее в кольцо, а затем делаете в этом кольце одну половину оборота и склеиваете концы вместе. Теперь у вас есть лента Мёбиуса.
Геометрические законы, которые обуславливают эту особенность, включают в себя:
- Нечетное количество пересечений: создание ленты Мёбиуса требует нечетного количества пересечений, чтобы каждая сторона ленты стала видимой. Если бы мы делали четное количество пересечений, мы получили бы две стороны.
- Положительная и отрицательная поверхности: лента Мёбиуса имеет только одну сторону, потому что каждая точка на ее поверхности находится одновременно на внешней и внутренней стороне этой поверхности. В результате, если бы у ленты Мёбиуса были две стороны, мы бы наблюдали нарушение геометрических законов в связи с этой особенностью.
Таким образом, геометрические законы объясняют, почему лента Мёбиуса имеет только одну сторону. Эта особенность делает ее уникальной и вызывает интерес у математиков, физиков и людей, интересующихся геометрией.
Топологический аспект

Топологические свойства ленты Мебиуса можно объяснить следующим образом. Если бы мы взяли обычную полоску бумаги и склеили ее концы вместе, получив кольцо, у этой поверхности были бы две стороны - внешняя и внутренняя. Однако, если мы возьмем полоску бумаги и перед склеиванием ее вернуть, так что одна сторона будет повернута в другую сторону, то после склеивания мы получим ленту Мебиуса, у которой одна сторона.
Интересно отметить, что для ленты Мебиуса нет такого понятия, как внутренняя и внешняя сторона. Если взять карандаш и пройтись по поверхности ленты Мебиуса, то можно пройтись по каждой его точке без пересечения с другой стороной. Это свойство делает ленту Мебиуса уникальной и привлекательной для исследования в топологии и геометрии.
Таким образом, лента Мебиуса имеет только одну сторону из-за своей неориентируемой топологической структуры, которая делает ее особой и интересной для науки, искусства и применений в различных областях.
Свойства и характеристики

Первое важное свойство ленты Мёбиуса заключается в том, что она имеет только одну сторону. Это означает, что на самом деле лента Мёбиуса не имеет плоской внешней поверхности и не может быть развернута в двумерное пространство без перерезания или склеивания. При движении по поверхности ленты Мёбиуса можно пройти по всем ее точкам, даже если не менять направление.
Второе важное свойство ленты Мёбиуса – это ее неоднозначность. Если вы начнете отмечать точки на поверхности ленты Мёбиуса, то обнаружите, что лента имеет только одну грань. Если продолжить отмечать точки на поверхности ленты, они вернутся на исходную грань, а затем продолжат двигаться по другой стороне. Таким образом, лента Мёбиуса имеет бесконечное число граней и неоднозначность в определении внешней и внутренней сторон.
Третье важное свойство ленты Мёбиуса – она обладает пространственной кривизной. В двумерном пространстве кривизна определяется радиусом кривизны, который обычно является постоянным для плоских поверхностей. Однако лента Мёбиуса является неоднородной поверхностью с переменной кривизной в зависимости от точки. Это делает ленту Мёбиуса уникальной с точки зрения геометрии и математики.
Для понимания свойств и характеристик ленты Мёбиуса необходимо проводить математические и геометрические исследования. Но уже эти простые описания дают представление о ее удивительных свойствах и демонстрируют, почему лента Мёбиуса вызывает настолько большой интерес у ученых и математиков.
Применение в науке и технике

Лента Мёбиуса, с её уникальными свойствами, нашла своё применение в различных областях науки и техники, где требуется особая конфигурация и эффективность.
Одним из основных применений ленты Мёбиуса является создание электронных схем. Благодаря своей односторонности, лента Мёбиуса позволяет перемещать электроны только в одном направлении, что является ключевым фактором при создании микросхем и других электронных компонентов.
Большой интерес вызывает также применение ленты Мёбиуса в оптике. Благодаря своей уникальной структуре, она может использоваться для создания оптических волокон с повышенной пропускной способностью и низкой потерей сигнала. Такие волокна находят применение в телекоммуникационных системах, фиброоптических лазерах и других оптических устройствах.
Также, лента Мёбиуса применяется в аэронавтике и космической инженерии. Её уникальная структура позволяет улучшить аэродинамические характеристики аппаратов и снизить сопротивление воздушной среды. Благодаря этому, применение ленты Мёбиуса может способствовать разработке более эффективных и экономичных авиационных и космических технологий.
| Область применения | Примеры |
|---|---|
| Электроника | Создание микросхем и электронных компонентов |
| Оптика | Создание оптических волокон и устройств |
| Аэронавтика и космическая инженерия | Улучшение аэродинамических характеристик аппаратов |
Уникальность и особенности ленты мебиуса
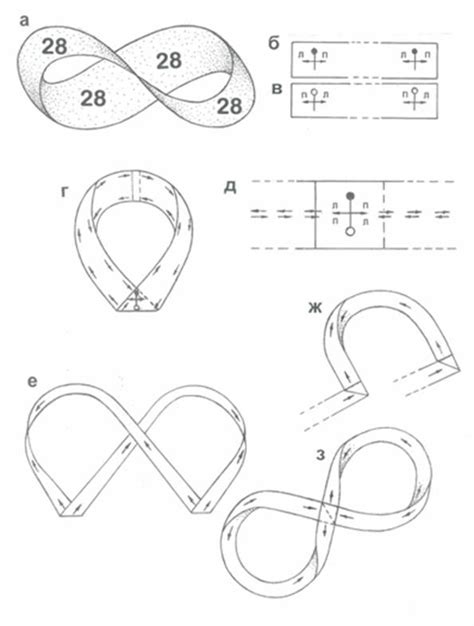
Эта лента получается путем взятия полоски бумаги, один конец которой сворачивается на 180 градусов, а затем соединяется с другим концом после сделанного поворота. Таким образом, при создании ленты Мёбиуса, мы получаем структуру, которая имеет только одну поверхность.
Интересный факт: лента Мёбиуса была открыта немецким математиком Августом Мёбиусом в 1858 году.
Эта математическая конструкция нашла не только применение в теории поверхностей, но и в различных областях: от искусства до техники. Ленту Мёбиуса можно увидеть в различных скульптурах, графическом дизайне, а также она используется в разработке современных конвейерных лент и лентопротяжных механизмов.
Сочетание уникальности и простоты ленты Мёбиуса, а также ее широкое применение, делают эту математическую конструкцию объектом интереса для изучения и использования в различных областях науки и техники.