Медиана - одно из основных понятий геометрии, использующееся в треугольниках. Она является отрезком, соединяющим вершину треугольника с серединой противолежащей стороны. Однако, мало кто знает, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, имеет фантастическое свойство - она равна половине гипотенузы. В этой статье мы рассмотрим математическое доказательство этого факта.
Для начала, представим наш прямоугольный треугольник на плоскости с координатами. Пусть вершины треугольника имеют координаты A(0, 0), B(0, b) и C(c, 0). Мы будем считать, что треугольник расположен в пространстве таким образом, что катеты параллельны осям x и y, а гипотенуза лежит под углом 45 градусов.
Затем, проведем медиану AM из вершины A, которая делит сторону BC пополам и пересекает гипотенузу в точке M. Давайте выразим координаты точек M и C через переменные m и n. Тогда координаты M будут M(c - n, n), а координаты C - C(c, 0). Используя формулу квадрата длины стороны треугольника, можем утверждать, что AM^2 = BM^2. Раскрывая квадрат скобок, получаем уравнение 2cm - c^2 = 2n^2. Важно заметить, что речь идет о квадратах длин сторон треугольника, а не самих длинах.
Каково доказательство равенства медианы половине гипотенузы?

Равенство медианы половине гипотенузы в прямоугольном треугольнике можно доказать с помощью геометрической интерпретации медианы и свойств прямоугольного треугольника.
Медиана – это отрезок, соединяющий вершину прямоугольного треугольника с серединой противолежащей стороны. Радиус вписанной окружности, проведенный до середины стороны, является медианой.
Гипотенуза – это самая длинная сторона прямоугольного треугольника. Она соединяет две вершины, не являющиеся прямыми углами.
Чтобы доказать, что медиана равна половине гипотенузы, воспользуемся свойствами подобных треугольников:
1. Рассмотрим равносильный прямоугольный треугольник со сторонами, равными удвоенным сторонам исходного треугольника. Его гипотенуза будет в два раза длиннее гипотенузы исходного треугольника.
2. В этом новом равносильном треугольнике также проведем радиус вписанной окружности до середины стороны. По свойству медианы, он будет равен половине стороны.
3. Полученный радиус окружности соответствует половине гипотенузы исходного треугольника.
Таким образом, доказано, что медиана прямоугольного треугольника равна половине гипотенузы.
Определение медианы и гипотенузы
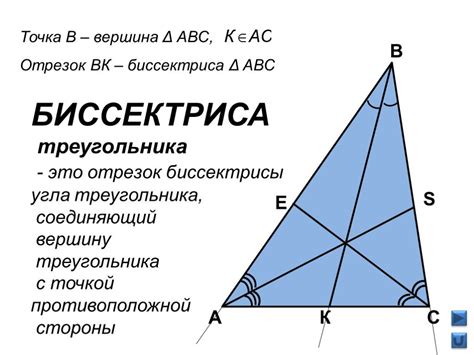
Гипотенуза - это самая длинная сторона прямоугольного треугольника, которая находится против прямого угла. Гипотенуза является основанием медианы и делит треугольник на два равных прямоугольных треугольника.
Важное свойство треугольника
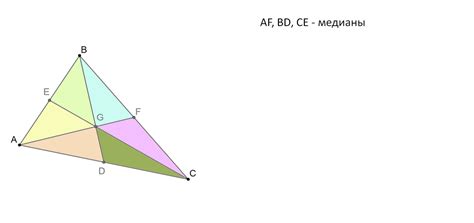
Доказательство на основе сходных треугольников

Заметим, что треугольники BCD и ABC являются сходными, так как у них углы при вершине C равны (прямой угол) и угол BCD равен углу ABC (по построению медианы). Из свойств сходных треугольников следует, что отношение длины сторон треугольников BCD и ABC равно отношению длины стороны BD к стороне AC.
Так как сторона BD является медианой, она делит сторону AC на две равные части, а значит, отношение длины стороны BD к стороне AC равно 1/2. Из равенства отношений сторон следует, что треугольники BCD и ABC подобны, и соответствующие стороны этих треугольников пропорциональны.
Так как сторона BC является гипотенузой прямоугольного треугольника ABC, она считается наибольшей стороной. Сторона BD, являющаяся медианой, находится между вершинами B и C. Следовательно, сторона BD будет меньше стороны BC.
Таким образом, мы получаем, что сторона BD, равная медиане, является половиной стороны BC, то есть медиана треугольника равна половине его гипотенузы.
Доказательство на основе расстояний

Для доказательства равенства медианы треугольника половине его гипотенузы можно использовать понятие расстояния.
Пусть треугольник ABC имеет стороны a, b и c, а медиана AM катета AC - длину m.
Рассмотрим треугольник ABM, в котором AM - медиана и BM - гипотенуза. По теореме Пифагора получаем:
BM^2 = AB^2 + AM^2
BM = с, AB = a, AM = m
c^2 = a^2 + m^2
Так как треугольник ABC - прямоугольный, то с = √(a^2 + b^2), так что:
√(a^2 + b^2)^2 = a^2 + m^2
a^2 + b^2 = a^2 + m^2
b^2 = m^2
Таким образом, получаем, что m = b.
Следовательно, медиана AM катета AC равна половине гипотенузы AB.
Практическое применение доказательства

Доказательство, основанное на равенстве медианы треугольника половине его гипотенузы, имеет важное практическое применение в геометрии и тригонометрии.
Одной из основных областей использования этого доказательства является решение задач, связанных с треугольниками. Зная длину гипотенузы и одну из медиан, мы можем вычислить длины оставшихся сторон треугольника, а также его площадь.
Кроме того, доказательство может быть использовано для нахождения высоты треугольника, проведенной из вершины, противоположной гипотенузе. Для этого достаточно знать длину гипотенузы и одну из медиан.
Также стоит отметить, что знание равенства медианы половине гипотенузы может помочь в решении задач, связанных с построением треугольников. Например, если нам известна длина гипотенузы и одна из медиан, мы можем построить треугольник, удовлетворяющий этим условиям.
В целом, доказательство равенства медианы половине гипотенузы является важным инструментом для работы с треугольниками и позволяет решать широкий спектр задач, связанных с этой геометрической фигурой.