Математика – это наука о числах и их взаимоотношениях. Все мы знаем, что минус на плюс равно минус, а плюс на минус тоже равно минус. Однако, почему минус на минус равно плюс и вызывает у нас необычное ощущение? Давайте разберемся в этой малоизвестной математической теории.
В основе понимания почему минус на минус равно плюс лежит алгебраическая система чисел. Эта система определяет операции над числами и их свойства. Одним из свойств алгебраической системы является закон сохранения знаков операций.
Складывать положительные числа мы умеем, а вот отрицательные – это уже вызывает затруднение. Однако дело в том, что если мы умеем складывать положительные числа, то мы уже изучили множество знакообразующих элементов и готовы перейти к минусам. И тут нам на помощь приходит правило, которое гласит: «Минус на минус равно плюс». Это правило разрешает нам умножать отрицательные числа.
Математические основы теории

Концепция минус на минус равно плюс базируется на математических основах алгебры и арифметики. Для полного понимания этого феномена необходимо знание основных математических понятий.
Минус (-) и плюс (+) - это две основные операции, используемые в арифметике. Операция минус обозначает вычитание, а операция плюс - сложение. В математике мы работаем с числами, которые могут быть положительными, отрицательными или нулевыми.
Числа имеют свойства, которые позволяют нам проводить различные операции с ними. Одно из таких свойств - свойство противоположного числа. Если число а является положительным, то его противоположным числом будет число -а. И наоборот, если число а является отрицательным, то его противоположным числом будет число -а.
Когда мы вычитаем число из другого числа, это можно интерпретировать как сложение с противоположным числом. Если мы имеем, к примеру, число 5 и вычитаем из него число 3, то это можно записать как 5 + (-3). В результате получается число 2. Простым примером данного случая является уравнение 5 - 3 = 2.
Теперь рассмотрим случай, когда мы вычитаем отрицательное число. Если у нас есть, к примеру, число 5 и мы вычитаем из него число -3, то это можно записать как 5 + 3. В результате получится число 8. Пример данного случая - 5 - (-3) = 8. Можно заметить, что в обоих случаях, когда мы вычитаем отрицательное число, результат положителен.
Исторический экскурс

Вопрос о том, почему минус на минус равно плюс, вызывает любопытство уже на протяжении долгого времени. Несмотря на то, что в математике принято обозначать отрицательные числа и проводить с ними операции, объяснение этого явления в рамках математической теории оказывается сложной задачей.
Однако, чтобы понять, почему минус на минус равно плюс необходимо прибегнуть к историческому экскурсу. Вероятно, первые вопросы об отрицательных числах возникли еще в древнегреческом мире. Уже тогда появилось представление о долгах, то есть об отрицательной стороне числа.
Один из первых формальных подходов к отрицательным числам был разработан в XII веке арабским математиком Мухаммедом Ибн Муса аль-Хорезми. Он использовал понятие противоположности чисел, с помощью которого было возможно вычислять суммы и разности.
| Год | Событие |
|---|---|
| 1545 | Жером Кардано вводит формулы для нахождения квадратных корней отрицательных чисел |
| 1683 | Имгард Герберт вводит комплексные числа и разработывает их арифметику |
| 1787 | Леонард Эйлер применяет понятия комплексных чисел и иррациональных чисел для объяснения необычных свойств математических операций |
В течение следующих веков комплексные числа и их арифметика стали фундаментальной базой для понимания и обозначения отрицательных чисел. Леонард Эйлер сумел объяснить странное поведение отрицательных чисел с помощью комплексных чисел и иррациональных чисел.
Таким образом, исторический экскурс помогает нам лучше понять, как и почему существует правило, что минус на минус равно плюс. Открытия и разработки ученых помогли установить математическую теорию, которая на сегодняшний день считается верной.
Положительное и отрицательное

Чтобы понять, почему минус на минус равно плюс, нам необходимо разобраться в особенностях работы положительных и отрицательных чисел.
В математике существует понятие числовой оси, на которой положительные числа располагаются справа от нуля, а отрицательные числа - слева. Когда мы складываем положительное число с положительным, получаем результат больше нуля. Например, 4 + 3 = 7.
Если же мы складываем положительное число с отрицательным, ситуация меняется. При сложении чисел разных знаков мы вычитаем из большего числа по модулю меньшее число, соответствующего знаку, и получаем число отрицательное. Например, 5 + (-2) = 3.
Но что происходит, когда мы складываем отрицательное число с положительным или два отрицательных числа?
Когда мы складываем отрицательное число и положительное число, сначала мы вычитаем из положительного числа по модулю отрицательное число, а затем меняем знак результата. Например, (-4) + 2 = -2. Таким образом, мы можем сказать, что (-4) + 2 = 2 - 4 = -2.
Также, когда мы складываем два отрицательных числа, мы производим умножение обоих чисел на -1, а затем складываем их по правилу сложения положительных чисел. Например, (-4) + (-2) = -6.
Итак, в математике существуют определенные правила сложения чисел разных знаков, которые позволяют нам объяснить, почему минус на минус равно плюс.
Отрицательные числа в алгебре

Отрицательные числа в алгебре играют важную роль и имеют свои особенности. Они помогают решать различные задачи и давать точные ответы в математике.
Отрицательное число - это число, меньшее нуля. Оно обозначается знаком "минус" перед числом. Например, -5, -1/2, -√2.
Отрицательные числа в алгебре используются в различных ситуациях. Например, при вычитании. Если у нас есть число 10 и мы отнимаем от него 5, то получим 5. А если мы отнимаем от 10 -5, то получим 15. Таким образом, отрицательное число позволяет нам выражать отрицательное изменение.
Отрицательные числа также используются при решении уравнений. Например, если у нас есть уравнение x^2 - 4 = 0, то решение этого уравнения будет x = ±2. Здесь плюс и минус перед числом обозначают два разных решения.
Отрицательные числа также удобно использовать для обозначения направлений в пространстве или на числовой оси. Например, если имеется движение вправо на 3 единицы, то движение влево на 3 единицы можно обозначить как -3.
Сумма отрицательного числа и положительного числа также будет отрицательным числом. Например, -4 + 3 = -1. Такая операция называется вычитанием.
Таким образом, отрицательные числа в алгебре играют важную роль и помогают нам решать различные задачи. Они позволяют выражать отрицательное изменение, находить решения уравнений, обозначать направления и проводить различные математические операции, такие как вычитание.
Примеры и доказательства
Для лучшего понимания того, почему минус на минус равно плюс, рассмотрим несколько примеров и докажем этот факт формально.
Пример 1: Раскроем скобки в выражении (-1)(-3):
(-1)(-3) = -1*(-3)
Умножаем минус единицу на минус три:
-1*(-3) = 3
Таким образом, (-1)(-3) равно 3.
Пример 2: Рассмотрим выражение (-2)(-4):
(-2)(-4) = -2*(-4)
Умножаем минус два на минус четыре:
-2*(-4) = 8
Значит, (-2)(-4) равно 8.
Доказательство: Докажем формально, что минус на минус равно плюс.
Предположим, что -(-x) = y, где x и y - произвольные числа.
Тогда у нас есть:
(-1)(-x) = y
Раскроем скобки:
-1*(-x) = y
Умножаем минус единицу на минус икс:
x = y
Таким образом, доказано, что минус на минус равно плюс, или -(-x) = x.
Применение минуса на минус в реальной жизни
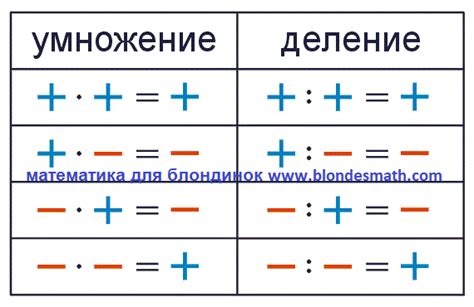
Математическая теория утверждает, что минус на минус равно плюс. Однако, может показаться, что такое применение минуса на минус ничего не имеет общего с реальной жизнью. Однако, на самом деле, ситуации, в которых применяется данное правило, встречаются довольно часто.
Возьмем, например, ситуацию с банковскими счетами. Когда мы берем кредит на определенную сумму, на нашем банковском счете становится отрицательное число, так как мы должны вернуть кредит. Если в этот момент мы снимаем еще деньги со счета, то это также считается минусом. Однако, если в следующий день мы внесем на счет деньги, то счет станет положительным. Таким образом, минус на минус дают плюс.
Другой пример можно найти в физике. Когда две силы, направленные в противоположные стороны, действуют на тело, то считается, что силы складываются. Если обе силы идут в одном направлении, то они складываются, итогом будет положительная сила. Однако, если одна из сил изменит направление, то она будет представлена с отрицательным знаком. В данном случае, минус на минус также будет равно плюсу.
Таким образом, хоть на первый взгляд, применение минуса на минус может показаться чем-то абстрактным и не имеющим отношения к реальности, на самом деле, данная теория находит свое применение в различных сферах жизни, включая финансы и физику.