Модуль функции является одним из основных понятий в математике и имеет широкое применение в различных областях, включая физику, экономику и технику. Он позволяет получить абсолютное значение функции независимо от ее знака. Но почему модуль функции не дифференцируем в нуле?
Оказывается, ответ на этот вопрос связан с особенностями определения дифференцируемости функции. Дифференцируемость функции в точке означает, что значение ее производной в этой точке существует и является конечным. Однако, если рассмотреть график модуля функции, то можно увидеть, что его наклон меняется в точке нуль. Иначе говоря, в окрестности нуля график как бы "разворачивается", но без резкого пересечения оси абсцисс.
Эта особенность поведения графика модуля функции не позволяет определить значение производной в нуле. Фактически, в точке нуль функция не обладает локальной линейной аппроксимацией, при которой можно было бы найти касательную. Это связано с тем, что слева и справа от нуля функция имеет разные наклоны, что делает неоднозначным определение значения производной в этой точке.
Необходимость модуль функции
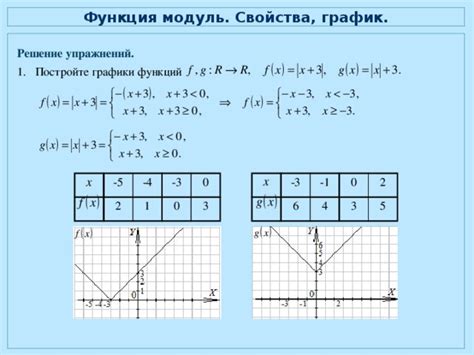
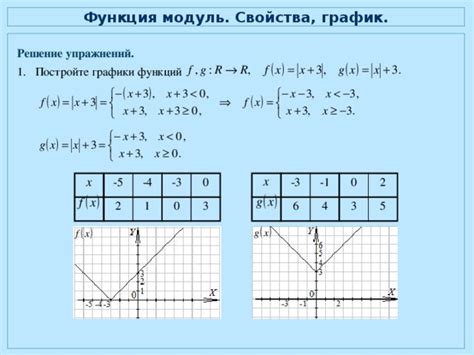
Один из ключевых моментов, по которому возникает необходимость использования модуля функции, - это возможность работать с отрицательными значениями и получать конечный и позитивный результат.
| Свойства функции модуля | Описание |
|---|---|
| 1. Модуль числа | Модуль числа определяется как его абсолютное значение. Используется для определения расстояния между числами или для получения позитивного значения. |
| 2. Решение уравнений | Модуль функции широко применяется для решения различных уравнений. Он позволяет найти все значения переменной, при которых модуль функции равен заданному числу. |
| 3. Графическое изображение | Модуль функции помогает строить графики, анализировать форму и свойства функции. Он используется для определения асимптот и точек перегиба, а также для изучения поведения функции в различных интервалах. |
| 4. Векторы | Модуль функции вектора является его длиной и используется в физике, механике и других науках. Он позволяет определить величину и направление вектора. |
Возможность нахождения расстояния
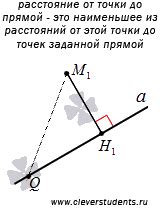
Для любых двух точек на координатной плоскости можно вычислить расстояние между ними, используя модуль функции. Это может быть полезно, например, при решении задач, связанных с определением расстояния между двумя городами на карте или при измерении расстояния между двумя точками на экране компьютера.
Кроме того, модуль функции позволяет упростить вычисления и избежать сложностей, связанных с определением знака функции. При нахождении расстояния по модулю не требуется учитывать положительное или отрицательное значение функции - достаточно взять абсолютное значение и получить нужный результат.
Таким образом, несмотря на то, что модуль функции не дифференцируем в нуле, его использование имеет множество практических применений и позволяет упростить вычисления расстояний между точками на координатной плоскости.
Решение уравнений с абсолютными значениями

Абсолютное значение функции представляет собой расстояние от нуля до заданной точки на числовой оси. Уравнение с абсолютными значениями содержит выражение внутри модуля функции, которое может быть равно положительному или отрицательному значению.
Для решения уравнения с абсолютными значениями мы можем использовать два подхода: графический и алгебраический. В графическом подходе мы строим график функции и определяем точки пересечения графика с осью абсцисс. В алгебраическом подходе мы рассматриваем два случая: когда выражение внутри модуля функции больше или равно нулю, и когда оно меньше нуля.
Пусть у нас есть уравнение |f(x)| = a, где f(x) - функция, a - заданное значение. Для начала рассмотрим случай, когда a больше или равно нуля. В этом случае уравнение превращается в два уравнения: f(x) = a и f(x) = -a. Решив каждое из этих уравнений отдельно, мы найдем значения переменной x, которые удовлетворяют исходному уравнению.
Теперь рассмотрим случай, когда a меньше нуля. В этом случае уравнение не имеет решений, так как абсолютное значение функции никогда не может быть отрицательным.
Таким образом, решение уравнений с абсолютными значениями заключается в разделении на два случая и решении каждого из них отдельно. Графический подход позволяет визуально представить решения, а алгебраический подход позволяет получить точные значения переменной x.
| Пример уравнения | Графическое решение | Алгебраическое решение |
|---|---|---|
| |2x - 3| = 5 | Построение графика функции и определение точек пересечения с осью абсцисс | Разделение на два случая: 2x - 3 = 5 и 2x - 3 = -5 |
| |x + 1| = -2 | Уравнение не имеет решений, так как абсолютное значение не может быть отрицательным | Нет решений |
Ограничения модуль функции
Однако, модуль функции имеет определенные ограничения, особенно в точке нуля. В точке нуля значение модуля функции полагается равным нулю, но сама функция не дифференцируема в этой точке.
При изучении дифференциального исчисления, дифференцируемость функции в данной точке означает, что ее производная определена в этой точке. Однако, при попытке найти производную модуля функции, оказывается, что она не определена в точке нуля. Это связано с тем, что в нуле производная модуля функции имеет разрыв, и значение производной меняется сразу с минус бесконечности на плюс бесконечность.
Таким образом, модуль функции является примером функции, которая не дифференцируема в нуле. Это ограничение может быть преодолено с помощью использования других математических методов, таких как производные с обобщенным определением или использование других видов функций, недифференцируемых в нуле.
Недифференцируемость в нуле
Однако, несмотря на то, что модуль функции гладкий и непрерывный, он не дифференцируем в нуле. Зачем же это происходит?
Проблема заключается в том, что модуль функции меняет знак при пересечении оси координат. Например, модуль функции f(x) = x меняет знак при x = 0. Это означает, что функция не имеет производной в этой точке.
Дифференцируемость функции в некоторой точке означает, что ее производная существует и является конечной. В случае модуля функции, производная в нуле не существует, так как функция меняет свое поведение и знак на этой точке.
Недифференцируемость модуля функции в нуле приводит к тому, что при наличии локального экстремума в этой точке, такой экстремум не может быть определен при помощи производной.
Это может вызывать определенные сложности при решении задач оптимизации и определении характеристик функции в нуле.
Таким образом, недифференцируемость модуля функции в нуле является одним из особых свойств этой математической конструкции и требует особого внимания при анализе и решении задач, связанных с модулем функции.



