Площадь и периметр - это два основных понятия, используемых в геометрии. Они описывают разные характеристики геометрических фигур. Но что именно они значат и в чем заключается их разница?
Площадь обозначает количество поверхности, занимаемое фигурой. Она измеряется в квадратных единицах, таких как квадратные метры или квадратные сантиметры. Площадь можно найти путем умножения длины и ширины фигуры или с использованием специальных формул для разных фигур, таких как прямоугольник, треугольник, круг и т.д. Площадь позволяет нам определить, насколько "заполнена" фигура.
Периметр, с другой стороны, представляет собой длину внешней границы фигуры. Он измеряется в единицах длины, таких как метры, сантиметры или дюймы. Найти периметр можно путем сложения всех сторон фигуры или с помощью соответствующих формул для разных типов фигур. Периметр дает нам представление о длине окружности фигуры или длине ее границы.
Вот и вся разница между площадью и периметром: первое измеряет площадь, занимаемую фигурой, а второе - длину ее границы. Эти две характеристики являются важными для изучения и анализа геометрических фигур и могут использоваться в различных сферах, включая архитектуру, строительство, урбанистику и другие.
Площадь и периметр: две разные величины
Площадь – это мера площади, которую занимает геометрическая фигура на плоскости. Она выражается в квадратных единицах и рассчитывается по формуле, зависящей от типа фигуры. Например, для прямоугольника площадь равна произведению длины одной стороны на длину другой стороны. Для круга площадь рассчитывается по формуле π*r², где π – математическая константа, а r – радиус круга.
Периметр – это сумма длин всех сторон геометрической фигуры. Он указывает на длину линии, ограничивающей фигуру. Периметр измеряется в единицах длины, таких как сантиметры или метры. Для прямоугольника периметр рассчитывается по формуле 2*(a+b), где a и b – длины сторон прямоугольника. Для круга периметр вычисляется по формуле 2*π*r, где π – математическая константа, а r – радиус круга.
Таким образом, площадь и периметр – это две разные характеристики геометрических фигур. Площадь определяет занимаемую площадь, а периметр – длину ограничивающей линии. Оба понятия имеют свои математические формулы для расчета и используются для характеристики и изучения геометрических фигур.
Площадь и периметр: основные понятия
Периметр - это сумма всех сторон фигуры. Это показатель, который характеризует длину замкнутой линии, описывающей фигуру. Он определяет, сколько длины необходимо пройти по контуру, чтобы обойти всю фигуру один раз. Например, для квадрата периметр - это сумма всех его сторон, для круга - длина окружности.
Площадь же - это показатель, который характеризует площадь поверхности фигуры. Он измеряет, сколько площади занимает фигура на плоскости. Например, для квадрата площадь - это площадь, ограниченная его сторонами, для круга - площадь, ограниченная его окружностью.
Важно отметить, что площадь и периметр различных фигур могут иметь разные значения, даже если их площади или периметры равны. Например, у прямоугольника со сторонами 2 м и 6 м площадь равна 12 м², в то время как у квадрата со стороной 3 м площадь также равна 9 м². Хотя площади разные, периметры этих фигур равны 16 м и 12 м соответственно.
Таким образом, площадь и периметр - это две важные характеристики фигур, которые помогают описать их размеры и свойства. Площадь измеряет поверхность, занимаемую фигурой, в то время как периметр измеряет длину контура фигуры. Оба этих понятия имеют свои уникальные задачи и применения в математике, строительстве, географии и других областях.
Площадь и периметр: определения и формулы
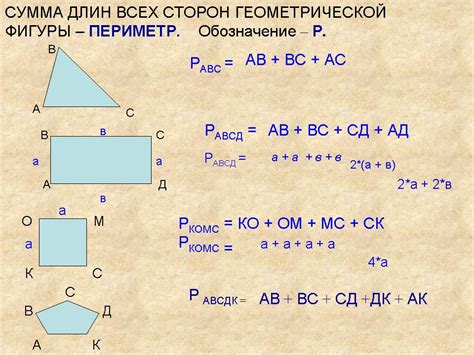
Периметр представляет собой сумму длин всех сторон фигуры. Он помогает нам измерить "величину границы" фигуры - длину внешнего периметра. Формулы для вычисления периметра различных фигур могут быть разными, например:
- Для прямоугольника периметр вычисляется по формуле: P = 2(a + b), где a и b - длины сторон прямоугольника.
- Для круга периметр вычисляется по формуле: P = 2πr, где π - математическая константа, равная приблизительно 3,14159, а r - радиус круга.
Площадь, с другой стороны, представляет собой меру площади внутри границы фигуры. Она позволяет нам измерить "заполненность" фигуры и вычислить количество площади в квадратных единицах. Формулы для вычисления площади также различаются:
- Для прямоугольника площадь вычисляется по формуле: S = a * b, где a и b - длины сторон прямоугольника.
- Для круга площадь вычисляется по формуле: S = πr2, где π - математическая константа, равная приблизительно 3,14159, а r - радиус круга.
Таким образом, площадь и периметр - это две разные характеристики фигур, которые помогают нам измерить их размеры и свойства. Периметр измеряет длину границы фигуры, а площадь - количество площади внутри границы. Зная эти определения и формулы, мы можем более точно описывать и сравнивать различные геометрические фигуры.
Площадь и периметр: как они рассчитываются?
Периметр - это сумма длин всех сторон фигуры. Например, для прямоугольника периметр равен двойной сумме длин его сторон (P = 2*(a+b)), а для круга периметр равен длине окружности (P = 2*pi*r).
Площадь, с другой стороны, измеряет поверхность фигуры. Она рассчитывается по-разному для разных фигур. Например, для прямоугольника площадь равна произведению длины и ширины (S = a*b), а для круга площадь рассчитывается по формуле S = pi*r^2, где r - радиус круга.
Важно отметить, что площадь и периметр не могут быть просто сравнены друг с другом. Например, у двух фигур с одинаковой площадью могут быть разные периметры. Это означает, что фигуры могут иметь одинаковые площади, но разные формы и размеры.
Таким образом, периметр и площадь являются важными концепциями в геометрии, которые помогают изучать и понимать фигуры. Зная, как рассчитывать площадь и периметр, можно более точно описывать и сравнивать фигуры в пространстве.
Площадь и периметр: назначение и применение
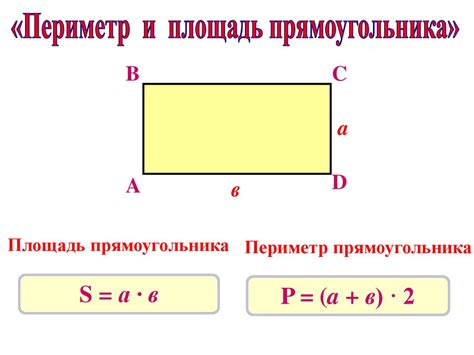
Периметр - это сумма всех сторон фигуры. Он позволяет определить длину замкнутой линии, окружающей фигуру. Мы можем вычислить периметр многоугольника, или окружности, зная длины его сторон или радиус. Периметр обычно используется для измерения длину забора, необходимого для ограждения участка, или для оценки длины ленты, необходимой для обрамления картин или зеркал.
Площадь - это мера внутренней поверхности фигуры. Она позволяет определить, сколько площади занимает фигура на плоскости. Для многоугольника или прямоугольника, площадь можно вычислить, умножив длину на ширину. Для круга, площадь можно вычислить, умножив квадрат радиуса на число пи. Площадь широко используется в архитектуре, строительстве, землеустройстве и других областях, где важно определить площадь площадки, помещения или участка.
Площадь и периметр: стоит ли их сравнивать?
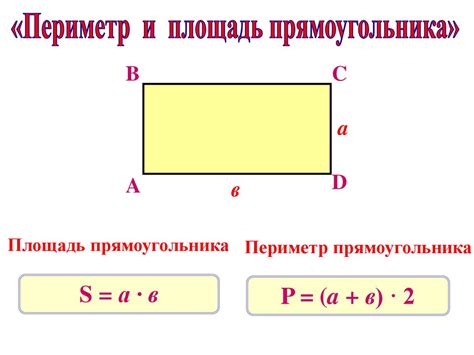
Периметр представляет собой сумму длин всех сторон фигуры. Он определяет, насколько длинным будет окружение этой фигуры. Например, для прямоугольника периметр равен удвоенной сумме его ширины и высоты. Периметр важен, когда речь идет о замкнутых фигурах, таких как круг, треугольник или квадрат. Он позволяет оценить длину ограждающей линии, что имеет значение, например, при расчете забора вокруг участка или нужного количества материала для облицовки.
Площадь, в свою очередь, является мерой площади, занимаемой фигурой на плоскости. Она измеряется в квадратных единицах (например, квадратных метрах или квадратных сантиметрах). Площадь определяет, насколько большой площади требуется для размещения фигуры. Например, для прямоугольника площадь равна произведению его ширины и высоты. Площадь часто используется для оценки площади помещений, площади участков земли или площади поверхности, которую нужно покрыть краской, тканью или другими материалами.
Таким образом, периметр и площадь предназначены для разных целей. Периметр обозначает размер окружения, а площадь - объем площади. Поэтому сравнивать эти два показателя некорректно и недостаточно для получения полного представления об объекте. Каждый из них имеет свое собственное значение и должен использоваться в соответствии с конкретными потребностями и задачами.



