Нормальное распределение - одно из самых распространенных и основных понятий в статистике. Именно оно лежит в основе многих аналитических методов и моделей. Но почему оно называется предельными?
Дело в том, что нормальное распределение, еще известное как распределение Гаусса, является особым видом вероятностного распределения. Именно оно представляет собой предельный случай распределения среднего арифметического множества случайных величин.
Нормальное распределение характеризуется своей симметричной и колоколообразной формой, где большинство значений сосредоточены вокруг среднего значения. Интересно, что распределение Гаусса можно встретить в самых разных областях - от физики и экономики до биологии и социологии.
Нормальное распределение: что это такое?
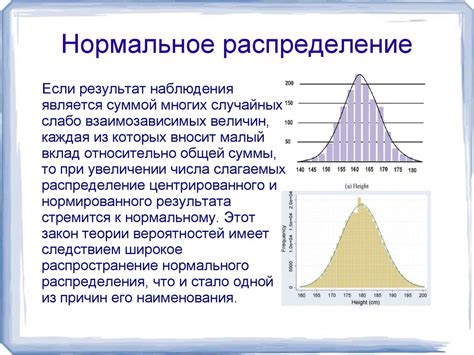
Предельное нормальное распределение, или также называемое предельное гауссово распределение, имеет особое значение в статистике и вероятностной теории. Оно возникает в случае, когда количество наблюдений или размер выборки стремится к бесконечности. При этом, предельное нормальное распределение позволяет аппроксимировать другие распределения и описывать вероятности их значений.
Особенностью предельного нормального распределения является его колоколообразная форма, которая стремится к идеальной колокольной кривой при бесконечно большом числе наблюдений. Оно характеризуется двумя параметрами - средним значением и стандартным отклонением.
Предельное нормальное распределение широко используется в различных областях, таких как статистика, физика, экономика и т.д. Великое значение имеет Центральная Предельная Теорема, которая утверждает, что сумма независимых случайных величин с конечными значениями будет стремиться к предельному нормальному распределению при определенных условиях.
Применение предельного нормального распределения позволяет проводить статистические тесты, оценивать вероятности событий, строить доверительные интервалы и многое другое. Также, оно обеспечивает надежную базу для дальнейшего анализа и прогнозирования данных.
Определение и особенности гауссова распределения
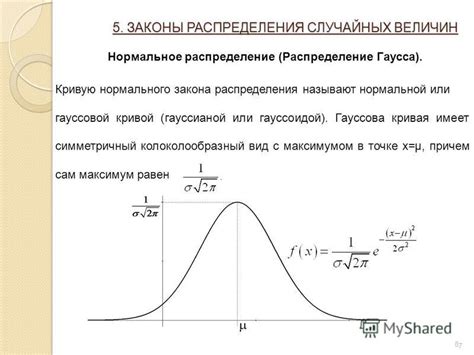
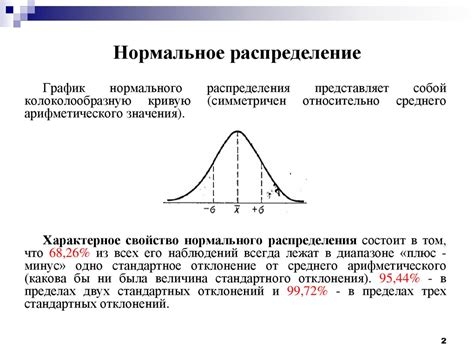
Основной особенностью гауссова распределения является его симметричность и колоколообразная форма графика плотности вероятности. Гауссово распределение характеризуется двумя параметрами: математическим ожиданием (средним значением) и стандартным отклонением.
Математическое ожидание гауссового распределения определяет его центр, а стандартное отклонение отражает его разброс. Чем больше стандартное отклонение, тем шире колоколообразная кривая графика и тем более разбросаны значения случайной величины.
Гауссово распределение обладает несколькими важными свойствами, которые делают его особенно полезным в статистическом анализе. Во-первых, оно хорошо описывает многие реальные случайные процессы, так как множество независимых случайных величин, складывающихся в одну, стремятся к нормальному распределению по центральной предельной теореме.
Во-вторых, гауссова функция имеет простую математическую формулу, что упрощает анализ и расчеты. Благодаря этому, многие статистические методы и тесты основаны именно на гауссовом распределении.
Наконец, гауссово распределение имеет множество приложений в различных областях науки, техники, экономики и других дисциплинах. Оно используется для моделирования случайных процессов, прогнозирования, анализа данных, классификации и многих других задач.
Почему гауссово распределение нормально?
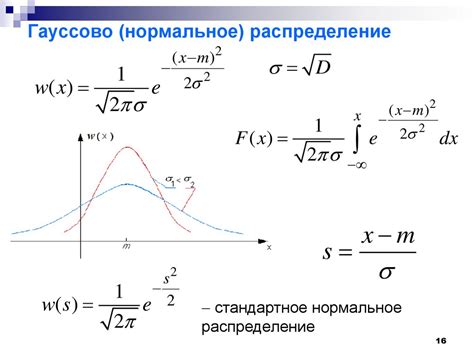
Почему же гауссово распределение так называется "нормальным"? Это обусловлено несколькими факторами.
Во-первых, гауссово распределение обладает множеством уникальных свойств, которые делают его нормальным в сравнении с другими вероятностными распределениями. Оно обладает симметрией, что означает, что вероятность находиться слева или справа от среднего значения равна. Форма распределения имеет колоколообразную кривую, с наибольшей вероятностью вблизи среднего значения. Также в гауссовом распределении вероятность уменьшается с удалением от среднего значения, что является характеристикой нормального поведения в природе и многих других процессах.
Во-вторых, ряд процессов в природе и поведении людей можно описать через гауссово распределение. Например, рост людей или вес представлен гауссовым распределением, что делает его естественным и нормальным в этом контексте.
Таким образом, гауссово распределение называется "нормальным" из-за своих уникальных свойств и способности описывать многие природные процессы. Оно является одним из основных и широко используемых распределений, что подтверждает его значимость и популярность в научных и практических приложениях.
Универсальность гауссового распределения
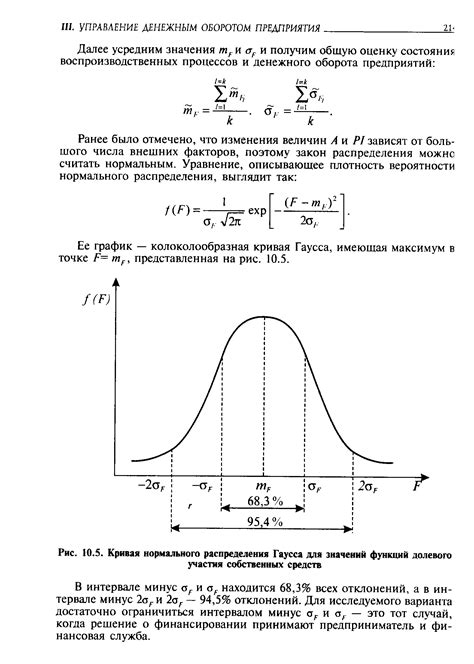
Одной из главных причин универсальной применимости гауссового распределения является центральная предельная теорема. Согласно этой теореме, сумма значений случайных независимых величин, имеющих любое распределение, приближается к нормальному распределению при достаточно большом количестве слагаемых. Это позволяет использовать нормальное распределение в качестве аппроксимации для любых случайных процессов. Благодаря этому свойству гауссовое распределение широко применяется в статистике и физике, где оно позволяет упростить сложные аналитические вычисления и сделать более точные предсказания.
Таким образом, гауссовое распределение обладает уникальными свойствами, которые делают его предельно подходящим для моделирования и анализа случайных процессов и данных. Универсальность гауссового распределения обусловлена его математическими свойствами, такими как центральная предельная теорема, симметричность и гладкость функции плотности вероятности. Поэтому нормальное распределение широко используется во многих областях науки и промышленности.
Предельное состояние нормального распределения
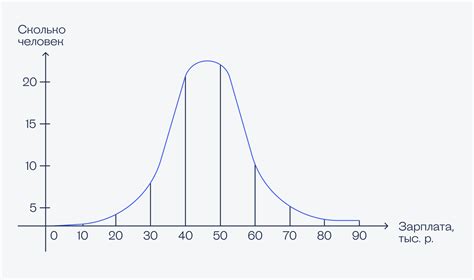
Предельное состояние нормального распределения, или предельное распределение, связано с идеей асимптотической нормальности. Иными словами, когда размер выборки стремится к бесконечности, распределение выборочного среднего будет стремиться к нормальному распределению.
Когда предельное состояние наиболее точно описывает данные?
Во-первых, предельное состояние наиболее точно описывает данные, когда они имеют симметричное распределение. Гауссова кривая является симметричной относительно среднего значения и достаточно широкой, чтобы охватить большинство данных. Это позволяет легко интерпретировать и сравнивать результаты среднего и стандартного отклонения.
Во-вторых, предельное состояние хорошо описывает данные, когда они подчиняются закону больших чисел. Закон больших чисел утверждает, что с увеличением числа наблюдений, среднее значение выборки будет стремиться к среднему значению в генеральной совокупности. Распределение Гаусса идеально соответствует этому закону и позволяет определить вероятность отклонения среднего значения от истинного.
Наконец, предельное состояние наиболее точно описывает данные, когда они не имеют явных выбросов или значительного скошенности в одну из сторон. Гауссово распределение считается "идеальным" в смысле отсутствия выбросов и скошенности, что делает его удобным для статистического анализа и моделирования данных.
Таким образом, предельное состояние, представленное нормальным распределением Гаусса, наиболее точно описывает данные, когда они имеют симметричное распределение, подчиняются закону больших чисел и не имеют выбросов или значительной скошенности.
Применение предельного состояния нормального распределения в практике
Предельное состояние нормального распределения, также известное как предельная теорема Гаусса, имеет широкое применение в различных областях практики, включая статистику, экономику, физику, биологию и многие другие.
Другим применением предельного состояния нормального распределения является моделирование физических и природных процессов. Многие процессы, такие как движение частиц в газе, диффузия вещества или случайные колебания в электрических цепях, могут быть описаны с использованием нормального распределения. Это позволяет упростить математическую модель и сделать точные и достоверные предсказания.
Также предельное состояние нормального распределения широко используется в экономических и финансовых моделях. Например, в моделях финансовых рынков предполагается, что изменения цен активов имеют нормальное распределение. Это позволяет моделировать риски и делать прогнозы на основе статистических методов.
В биологии предельное состояние нормального распределения может быть использовано для анализа различных явлений, таких как распределение телесных масс животных или концентрации веществ в организме. Это может помочь в понимании структуры и функций биологических систем.
Таким образом, предельное состояние нормального распределения играет важную роль в практике и находит применение во многих областях науки и техники, где требуется проводить анализ данных, моделировать процессы или делать прогнозы.



