Тригонометрия - это раздел математики, который изучает отношения между углами и сторонами треугольников. Окружность является одной из основных фигур, используемых в тригонометрии. Однако, почему окружность в тригонометрии обычно рассматривается с единичным радиусом?
Чтобы ответить на этот вопрос, необходимо понять, что в тригонометрии используются функции синус, косинус и тангенс, которые определены как отношения сторон в прямоугольном треугольнике. Отношения этих сторон не зависят от размеров треугольника, но зависят только от соответствующих углов.
Когда мы строим треугольник на единичной окружности, что означает радиус равным 1, координаты точек на окружности представляют собой значения синуса и косинуса углов. Поэтому, так как радиус равен 1, значения синуса и косинуса соответствуют длинам противолежащих и прилежащих к гипотенузе сторон прямоугольного треугольника, соответственно. Это позволяет нам легко вычислять значения синуса и косинуса углов, используя координаты точек на окружности.
Пределы при вращении
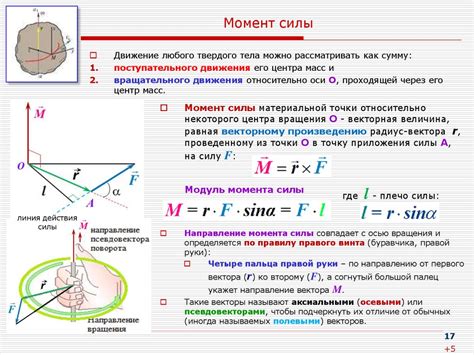
При изучении тригонометрии, особенно при вращении на плоскости, возникает вопрос о том, как изменяются значения тригонометрических функций при повороте. Для более глубокого понимания этого процесса, необходимо рассмотреть пределы при вращении.
Когда точка на окружности вращается вокруг начала координат, она пробегает некоторое расстояние по окружности. По мере вращения точки, угол поворота меняется от 0 до полного оборота вокруг окружности.
Пределы при вращении позволяют нам понять, как значения тригонометрических функций (синуса, косинуса, тангенса и т. д.) изменяются при различных углах поворота.
Если рассмотреть единичную окружность, то при повороте точки на угол 0 радиан, значения тригонометрических функций будут равны их начальным значениям. По мере поворота точки на более крупные углы, значения функций будут изменяться, однако останутся в пределах от -1 до 1.
Таким образом, единичная окружность играет важную роль в тригонометрии, поскольку она позволяет оценить изменение значений тригонометрических функций при различных углах поворота.
Связь с единичным треугольником
Рассмотрим единичный треугольник на плоскости. Одна из его сторон лежит на оси X, а другая на оси Y. Вершина треугольника находится в начале координат (0,0).
Таким образом, длины сторон единичного треугольника составляют 1 единицу. По определению, синус угла α равен отношению длины противоположной стороны к гипотенузе, а косинус угла α равен отношению длины прилегающей стороны к гипотенузе.
Вспомним, что круг радиусом 1 единица содержит все точки (х, у), удовлетворяющие уравнению x^2 + y^2 = 1. В этих координатах x и у образуют пару синуса и косинуса угла α, поэтому точка (х, у) на окружности соответствует синусу и косинусу угла α.
Таким образом, окружность единичного радиуса и единичный треугольник тесно связаны друг с другом: точки на окружности соответствуют значениям синуса и косинуса в соответствующих углах единичного треугольника. Эта связь имеет большое значение в тригонометрии и находит применение во многих областях науки и техники.
Удобство расчетов

Используя единичную окружность, мы можем легко вычислять значения тригонометрических функций для любого угла. Радиус окружности равен 1, поэтому координаты точек на окружности суть пары чисел (cos(α), sin(α)), где α - угол, измеренный в радианах. Это облегчает вычисление функций cos(α) и sin(α) для различных углов, так как необходимо только знать значение угла.
Например, для угла в 30 градусов, мы можем найти точку на единичной окружности, соответствующую этому углу. Затем, используя значение координаты x, мы можем найти значение cos(30) и, используя значение координаты y, мы можем найти значение sin(30). Простой и наглядный подход.
Кроме того, использование единичной окружности позволяет нам обобщить результаты и формулы для тригонометрических функций на любые углы. Мы можем проводить аналогии и устанавливать связи между различными углами, используя тригонометрические функции на единичной окружности.
В итоге, удобство расчетов с использованием единичной окружности является одним из основных факторов ее значимости в тригонометрии.
Отношения сторон
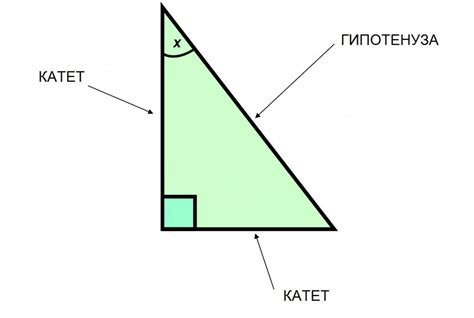
Окружность с радиусом, равным единице, представляет собой простую и легко визуализируемую геометрическую форму. Ее центр находится в начале координат, а радиус является основой для построения треугольников и расчета отношений сторон в них.
Обозначения, которые используются для обозначения отношений сторон, такие как синус (sin), косинус (cos) и тангенс (tg), являются геометрическими отношениями между сторонами треугольника и его углами. Например, синус угла - это отношение противолежащего катета к гипотенузе прямоугольного треугольника.
Используя единичную окружность, мы можем определить эти отношения для всех углов от 0 до 360 градусов. Это позволяет нам анализировать и вычислять значения геометрических отношений для различных углов, что является важным для решения задач в физике, математике и инженерии.
Таким образом, выбор единичной окружности в тригонометрии обусловлен ее простотой и удобством для изучения отношений сторон в прямоугольном треугольнике. Она позволяет нам вычислять и анализировать значения sin, cos и tg для любого угла на окружности.
Геометрическая интерпретация
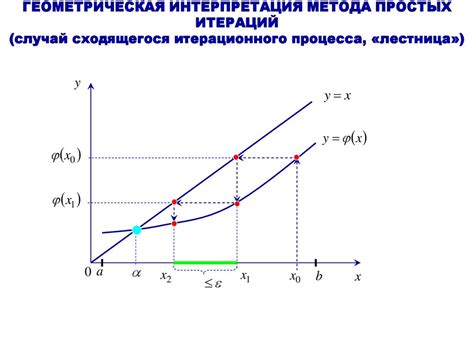
В тригонометрии окружность с центром в начале координат и радиусом 1 играет важную роль. Это связано с геометрической интерпретацией тригонометрических функций.
Рассмотрим точку на окружности с углом α между положительным направлением оси OX и лучом, соединяющим начало координат и данную точку. Такая точка имеет координаты (cos α, sin α).
Тригонометрические функции, такие как синус (sin) и косинус (cos), могут быть определены как значения соответствующих координат точек на окружности с определённым углом α.
На основе этой геометрической интерпретации, можно объяснить, почему окружность единичная в тригонометрии. Если радиус окружности был бы другим, значение тригонометрических функций тоже бы изменилось, что усложнило бы вычисления и использование этих функций.
Обобщение на произвольные окружности

В предыдущем разделе мы рассматривали окружность единичного радиуса в тригонометрии. Но что происходит, если мы хотим использовать произвольную окружность?
Оказывается, что все основные свойства и формулы тригонометрии также справедливы для произвольных окружностей. Мы всегда можем привести произвольную окружность к единичной путем масштабирования и сдвига координат. Это означает, что мы можем использовать углы и тригонометрические функции для любой окружности.
Когда мы говорим о произвольных окружностях, мы должны помнить о двух важных понятиях - радиусе и центре окружности. Радиус - это расстояние от центра окружности до любой точки на окружности. Чтобы определить угол для произвольной окружности, мы используем центр окружности и две точки - начало и конец дуги, на которую мы смотрим.
Также стоит отметить, что для произвольных окружностей тригонометрические функции могут принимать значения, не ограниченные от -1 до 1, так как радиус окружности может быть любым числом. Для работы с произвольными окружностями мы также можем использовать формулы для нахождения синуса, косинуса и тангенса, но теперь значения этих функций будут зависеть от радиуса окружности.
Таким образом, мы можем обобщить понятия и формулы тригонометрии на произвольные окружности, применяя их к центру и радиусу окружности. Это расширяет область применения тригонометрии и позволяет нам работать с различными окружностями в математике и физике.



