Параллелограмм - это геометрическая фигура, у которой противоположные стороны параллельны друг другу. Однако, несмотря на свою симметричную форму, параллелограмма не имеет ни одной оси симметрии. Ось симметрии - это воображаемая линия, которая делит фигуру на две одинаковые по форме и размеру части.
Параллелограмм не имеет оси симметрии, поскольку его форма не является зеркально симметричной. Если мы попытаемся провести ось симметрии через параллелограмм, то увидим, что его противоположные стороны находятся на разных расстояниях от этой оси. Таким образом, фигура разбивается на две неравные части, которые нельзя совместить друг с другом путем вращения или отражения.
Однако, несмотря на отсутствие оси симметрии, параллелограмм все равно обладает определенными свойствами симметрии. Например, если мы проведем диагонали внутри параллелограмма, то эти диагонали поделятся пополам и будут пересекаться в точке, которая является центром симметрии фигуры. Также, параллелограмм обладает осью вращения, которая проходит через центр симметрии и перпендикулярна его диагоналям.
Форма и свойства параллелограмма
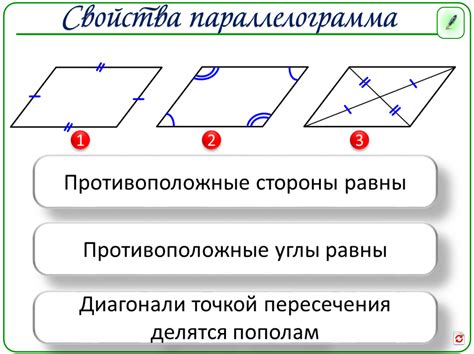
Важными свойствами параллелограмма являются:
- Периметр: сумма длин всех сторон параллелограмма.
- Площадь: произведение длины одной из сторон на высоту, опущенную на эту сторону.
- Диагонали: отрезки, соединяющие противоположные вершины параллелограмма.
- Углы: каждый угол параллелограмма равен сумме двух смежных углов.
- Диагонали: отрезки, соединяющие противоположные вершины параллелограмма.
Также стоит отметить, что параллелограмм не имеет оси симметрии. Это означает, что нельзя провести прямую линию, которая разделит фигуру на две равные части. При этом, параллелограмм обладает двумя осями симметрии - каждая пара противоположных сторон параллелелограмма является осью симметрии.
Понятие оси симметрии
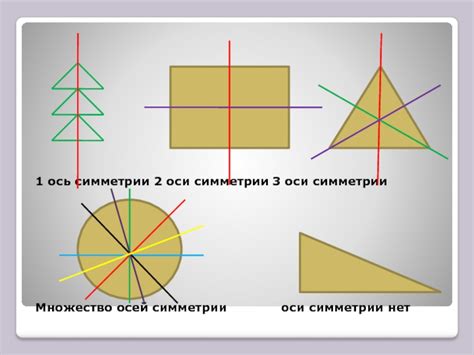
Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны. Он имеет две пары равных сторон и две пары параллельных сторон. Таким образом, параллелограмм не имеет оси симметрии. Это означает, что нельзя провести линию, такую что половина фигуры отразится в ней точно так же, как вторая половина.
Отсутствие оси симметрии связано с параллельностью сторон параллелограмма, которая делает его форму неравномерной относительно вертикальной или горизонтальной линии. Таким образом, в параллелограмме невозможно найти такую линию, проходящую через центр фигуры, которая делит его на две идентичные половины.
Соответствие формы параллелограмма и оси симметрии
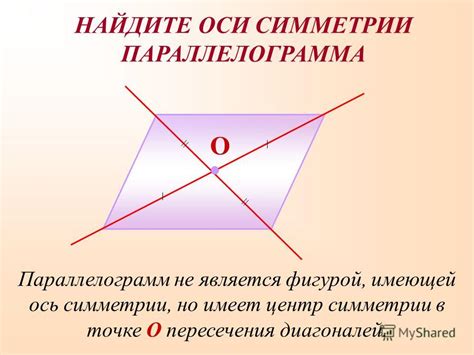
Ось симметрии - это линия, которая разделяет фигуру на две половины, симметричные относительно этой линии. Каждая точка фигуры и ее симметричная ей точка относятся друг к другу так, как если бы они были отражены относительно оси симметрии.
Параллелограмм обладает двумя осями симметрии - осью, проходящей через середину параллельных сторон, и осью, соединяющей середины диагоналей. Однако, осевая симметрия параллелограмма определена только для некоторых его частных случаев.
Если параллелограмм является прямоугольником, то он будет обладать двумя осями симметрии - и по горизонтали, и по вертикали. В этом случае фигуру можно разделить на четыре равные части. Но общий параллелограмм не обладает такими свойствами.
Чтобы найти ось симметрии параллелограмма, можно провести диагонали фигуры и при помощи них определить центр симметрии. Однако, в общем случае, параллелограмм не имеет одной оси, по которой он бы симметричен.
Таким образом, параллелограмм, хотя и обладает определенными осевыми симметриями в некоторых своих частных случаях, в общем случае не имеет оси симметрии.
Общие свойства параллелограмма и оси симметрии
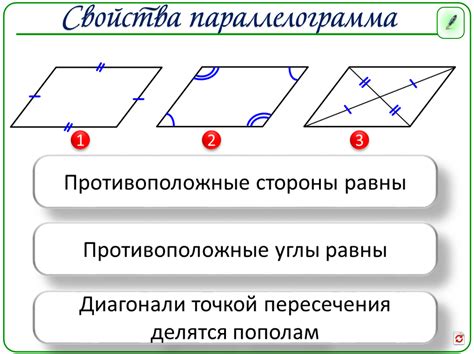
Параллелограмм не имеет оси симметрии. Ось симметрии - это линия, которая делит фигуру на две равные половины, симметричные относительно этой линии. В случае параллелограмма, такая линия отсутствует, поскольку его стороны не симметричны по отношению к какой-либо оси.
Однако, параллелограмм обладает рядом других интересных свойств:
- Диагонали параллелограмма делятся пополам.
- Сумма углов параллелограмма равна 360 градусов.
- Стороны параллелограмма равны и параллельны, что делает его подходящим для изучения законов проективной геометрии.
- Если в параллелограмме один из углов прямой, то все его углы прямые.
- Площадь параллелограмма можно вычислить, умножив длину одной его стороны на высоту, опущенную на эту сторону.
Изучение параллелограмма и его свойств помогает развить геометрическое мышление, а также применять полученные знания в практических задачах.