Статистика – наука о сборе, анализе, интерпретации, представлении и оценке данных, характеризующих массовые явления. Она является одной из важных дисциплин в области математической статистики и науки о данных.
Суть статистики заключается в том, чтобы изучать и описывать все тенденции и закономерности, которые прослеживаются в больших объемах информации. Она помогает выявлять взаимосвязи между различными переменными и делает возможным прогнозирование и принятие обоснованных решений на основе имеющихся данных.
В современном мире статистика играет ключевую роль в различных областях, таких как экономика, социология, медицина, инженерия и другие. Она позволяет изучать явления на основе конкретных данных, делая исследования объективными и оптимизируя процессы развития и управления.
Основными методами статистики являются сбор данных, их анализ и интерпретация. Статистические методы помогают описать данные с помощью различных статистических показателей, построить графики и диаграммы для более понятного представления информации, а также проводить статистическое моделирование для прогнозирования будущих явлений.
Статистика: изучение массовых явлений и их анализ

Основные задачи статистики включают сбор и обработку данных, изучение структуры и изменений в массовых явлениях, анализ причинно-следственных связей, определение степени достоверности результатов и т. д.
Для проведения статистического анализа используются различные методы, такие как сведение данных в таблицы, графическое представление информации, расчет основных показателей (среднее значение, медиана, дисперсия и т. д.), построение зависимостей и прогнозирование.
Одно из главных достоинств статистики – это ее объективность. Статистические данные основываются на фактических наблюдениях и измерениях, что позволяет получить объективную картину массовых явлений.
Статистика применяется во многих областях человеческой деятельности – от экономики и социологии до медицины и экологии. С ее помощью можно изучить и анализировать различные явления, например, рыночные тенденции, социальные процессы, патологии здоровья популяции и др.
Статистика позволяет находить закономерности, выявлять проблемы и находить эффективные решения. Она помогает принимать обоснованные решения на основе фактов и дает возможность предсказывать развитие ситуации.
Таким образом, статистика является важным инструментом в изучении массовых явлений и их анализе. Она позволяет получить объективные данные, выявить закономерности и прогнозировать развитие ситуации, что является необходимым для принятия решений в различных областях деятельности.
Характеристики и применение статистики

Основными характеристиками статистики являются:
- Среднее значение: показатель, который позволяет определить среднюю величину наблюдаемого явления. Среднее значение вычисляется путем суммирования всех значений и деления на их количество.
- Дисперсия: мера разброса значений относительно среднего значения. Дисперсия позволяет оценить, насколько значения отличаются друг от друга.
- Стандартное отклонение: корень из дисперсии. Оно показывает, насколько значения отклоняются от среднего значения и является мерой разброса данных.
- Медиана: значение, которое разделяет датасет на две равные части. Медиана позволяет определить "среднее" значение в наборе данных, игнорируя выбросы и экстремальные значения.
Статистика находит применение во многих областях жизни:
- В экономике: статистика помогает анализировать и прогнозировать экономические явления, такие как инфляция, безработица и рост ВВП.
- В медицине: статистика позволяет исследователям анализировать эффективность новых лекарств и методов лечения, а также определять факторы, влияющие на здоровье пациентов.
- В социологии: статистика используется для изучения социальных явлений, таких как рождаемость, смертность, уровень образования и качество жизни.
- В маркетинге: статистика позволяет оценить эффективность рекламных кампаний, предсказать тренды и понять поведение потребителей.
- В науке и исследованиях: статистика используется для анализа данных, сравнения групп, проверки гипотез и построения моделей.
Основные характеристики и применение статистики позволяют получать объективные данные, проводить анализ и принимать обоснованные решения в различных областях жизни.
Основные принципы статистического анализа

Основными принципами статистического анализа являются:
1. Случайность: В статистике предполагается, что изучаемые явления являются случайными. Данные, полученные в ходе наблюдений или экспериментов, представляют собой случайные величины, которые могут меняться измерениями.
2. Вероятность: Статистический анализ базируется на теории вероятностей, которая позволяет определить вероятность различных исходов и событий. Вероятностные методы используются для оценки статистической значимости результатов и для принятия статистических решений.
3. Вариация: В статистике учитывается вариация данных. Различные наблюдения или измерения могут отличаться друг от друга, и статистический анализ позволяет оценить степень этой вариации и определить ее значимость.
Методы сбора и обработки данных

Одним из основных методов сбора данных является наблюдение. При этом данные собираются непосредственно наблюдением за явлениями или процессами. Наблюдение может быть непосредственным или опосредованным, когда данные фиксируют исследователи, а не сами объекты исследования.
Другим важным методом сбора данных является опрос. Опрос позволяет получить информацию напрямую от опрашиваемых. Опросы могут проводиться с использованием анкет, интервью, телефонных звонков или онлайн-форм. Важно грамотно составить вопросы и обеспечить анонимность опрашиваемых для получения достоверных результатов.
Также статистические данные могут быть представлены в виде таблиц, графиков или диаграмм. Это помогает визуализировать информацию и упростить ее восприятие. Графические представления позволяют проанализировать данные и выделить основные тенденции и закономерности.
Ознакомившись с различными методами сбора и обработки данных, можно составить надежную и объективную статистику, которая будет полезна для принятия решений в различных областях деятельности.
Интерпретация результатов статистического исследования

Основные шаги в интерпретации результатов статистического исследования:
1. Определение цели исследования. Первым шагом является определение цели исследования – что конкретно нужно выяснить на основе статистических данных. Цель может быть связана с описанием явления, выявлением зависимостей или сравнением групп. |
2. Сбор данных. Вторым шагом является сбор необходимых данных, которые будут анализироваться. Данные могут быть собраны с помощью опросов, экспериментов, наблюдений или из социальных и экономических источников. |
3. Анализ данных. Третий шаг включает анализ числовых данных, проверку гипотез и выявление основных характеристик изучаемого явления. Важно провести статистические тесты и оценить значимость полученных результатов. |
4. Толкование результатов. |
5. Составление отчета. |
Важным фактором при интерпретации результатов статистического исследования является учет контекста и особенностей изучаемых явлений. Комбинирование количественного и качественного подходов может дать полнее и точнее представление о происходящих процессах и явлениях.
Выборка и ее репрезентативность
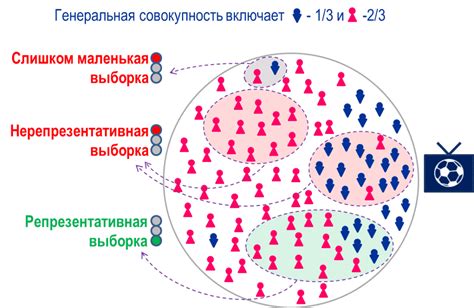
При изучении массовых явлений, статистики часто приходится работать с выборками данных вместо полной информации о популяции. Выборка представляет собой часть популяции, которая была отобрана для анализа.
Репрезентативность выборки – это ее способность правильно отражать характеристики популяции. Или по другому, выборка является репрезентативной, если ее статистические свойства, такие как среднее или дисперсия, близки к аналогичным параметрам популяции.
Основная задача при формировании выборки – выбрать такую ее часть, которая будет наилучшим образом отражать популяцию в целом. Для этого необходимо учитывать ряд факторов:
- Случайность отбора: выборка должна быть сформирована случайным образом из популяции. Это позволяет исключить возможное смещение результатов и обеспечить представительность выборки.
- Размер выборки: чем больше размер выборки, тем более точными будут полученные статистические показатели. Оптимальный размер выборки зависит от объема популяции и ожидаемой дисперсии изучаемого явления.
- Стратификация: метод разделения популяции на страты (группы) и формирование выборки путем случайного отбора участников из каждой страты. Этот подход позволяет учесть различные категории объектов, такие как пол, возраст или социальный статус, и получить более представительную выборку.
Репрезентативная выборка является основой для получения достоверной информации о популяции и проведения статистического анализа. Ее составление требует внимательного подхода и учета различных факторов, чтобы результаты исследования были максимально точными и значимыми.
Ошибки, возникающие при статистическом анализе
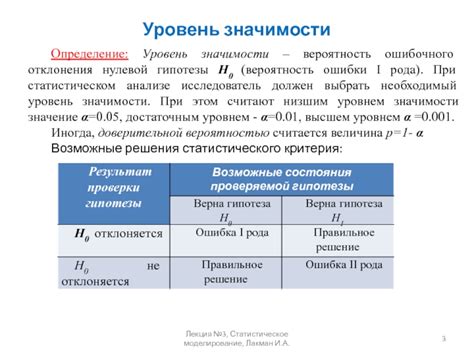
Вторая ошибка - недостаточный объем выборки. Чем меньше выборка, тем больше вероятность ошибки первого рода (ложноположительного результата) или второго рода (ложноотрицательного результата).
Третья ошибка - пропущенные данные. Пропуск данных может привести к искаженным результатам, так как это может привести к неправильной интерпретации данных и их некорректному использованию.
Статистические показатели и их оценка

Один из наиболее распространенных статистических показателей - это среднее значение (или среднее арифметическое). Оно вычисляется путем суммирования всех значений в выборке и деления получившейся суммы на количество элементов выборки.
Другим важным показателем является медиана. Она определяется путем упорядочивания значений выборки по возрастанию и выбора значения из середины. Если количество элементов выборки нечетное, то медиана будет равна значению, стоящему посередине. Если количество элементов выборки четное, то медиана будет равна среднему арифметическому двух средних значений.
Показателем разброса данных является стандартное отклонение. Оно позволяет оценить, насколько значения распределены вокруг среднего значения. Чем больше стандартное отклонение, тем больше разброс данных.



