Равнобедренный треугольник - это особый вид треугольника, у которого две стороны равны по длине. Такой треугольник имеет два равных угла, а также вершину, расположенную между этими сторонами. Но почему углы в равнобедренном треугольнике равны?
Ответ на этот вопрос лежит в его конструкции. Представьте, что имеется равнобедренный треугольник ABC, где AB = AC. От вершины A проведем высоту AD, которая пересекает сторону BC.
Высота делит треугольник на два прямоугольных треугольника ABD и ACD. В этих треугольниках гипотенузой является сторона AB или AC, а катетом – половина стороны BC.
Так как гипотенуза и один из катетов в обоих треугольниках равны, то противолежащие им углы одинаковы по величине. То есть, углы B и C в равнобедренном треугольнике всегда равны.
Определение равнобедренного треугольника
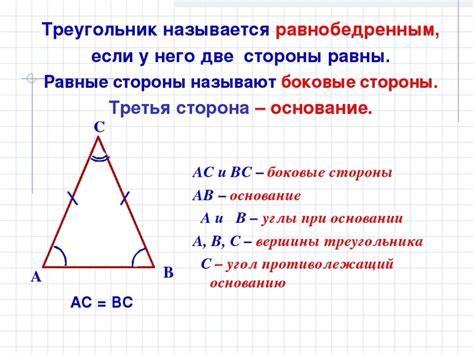
Другими словами, в равнобедренном треугольнике две стороны, называемые равными сторонами, и два угла, называемые равными углами, имеют одинаковые значения. Оставшийся угол в таком треугольнике называется основным углом, так как он образуется между двумя равными сторонами.
Основные свойства равнобедренного треугольника:
- Два равных угла обладают одинаковыми значениями.
- Два равных угла лежат напротив двух равных сторон.
- Основной угол равен сумме двух других углов.
- Биссектриса основного угла делит противоположную сторону на две равные части.
Равнобедренные треугольники встречаются в различных областях геометрии. Они имеют свои особенности и используются для решения задач и построений в различных геометрических конструкциях.
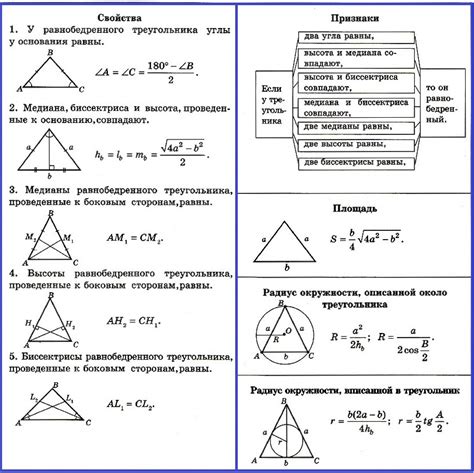
Основные свойства равнобедренного треугольника

1. В равнобедренном треугольнике, основания равны, что может быть доказано с использованием аксиомы о равенстве сторон.
2. Углы, прилежащие к равным сторонам, также равны. Это следует из теоремы о равенстве прилежащих углов равнобедренных треугольников.
3. Угол между равными сторонами равен. Это свойство следует из теоремы о равенстве углов против основания равнобедренного треугольника.
4. Перпендикуляры, опущенные из вершин равнобедренного треугольника, пересекаются в одной точке, которая является серединой основания.
Теорема об углах равнобедренного треугольника

Рассмотрим равнобедренный треугольник ABC с основанием AB и равными сторонами AC и BC. Пусть угол CAB и угол CBA обозначаются соответственно α и β.
Используя свойства треугольников, мы можем сделать следующие наблюдения:
| Свойство | Объяснение |
|---|---|
| Угол между боковой стороной и основанием | Угол BAC равен α, а угол ABC равен β |
| Сумма углов треугольника | Угол BAC + угол ABC + угол CAB = 180° |
| Углы с одной стороны равны | Угол BAC = угол ABC |
Из последнего свойства следует, что уголы у основания равнобедренного треугольника равны, то есть α = β. Доказательство теоремы по сути сводится к сравнению углов треугольника и использованию свойств равнобедренного треугольника.
Теорема об углах равнобедренного треугольника является важным результатом в геометрии и широко используется при решении различных задач и построений, связанных с равнобедренными треугольниками.
Доказательство теоремы
Рассмотрим равнобедренный треугольник ABC. Предположим, что AB=AC. Нам необходимо доказать, что углы B и C равны.
Шаг 1: Проведем биссектрису угла BAC и обозначим точку пересечения с основанием треугольника как P.
Шаг 2: Так как треугольник ABC равнобедренный, то AB=AC. Рассмотрим треугольники ABP и ACP. Они имеют равные стороны AB=AC (по условию) и BP=CP (отрезок BP является общим для двух треугольников).
Шаг 3: Так как треугольники ABP и ACP имеют равные стороны и равный общий отрезок BP=CP, то они равны по двум сторонам и общему углу (по теореме равенства треугольников).
Шаг 4: Значит, у них также равны углы BPA и CPA.
Шаг 5: В равнобедренном треугольнике BAP и CAP имеется два вертикальных угла (углы B и C, соответственно), которые являются парными углами.
Шаг 6: Следовательно, углы B и C в равнобедренном треугольнике ABC равны.
Доказательство завершено.
Примеры равнобедренных треугольников
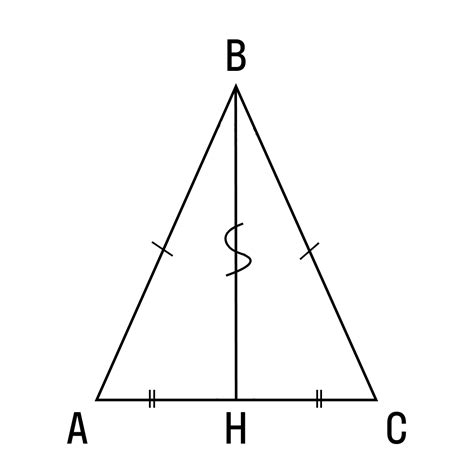
Вот несколько примеров равнобедренных треугольников:
Пример 1: Треугольник ABC, где AB = AC. В этом случае, угол B равен углу C.
Пример 2: Треугольник XYZ, где YX = YZ. Тогда угол X равен углу Z.
Пример 3: Треугольник PQR, где PQ = PR. В данном случае, угол Q равен углу R.
Равнобедренные треугольники встречаются в различных геометрических фигурах, а также в реальных объектах и структурах. Они широко используются в архитектуре, инженерии и других областях.
Применение равнобедренных треугольников в геометрии
1. Конструкция углов
| Пример | Описание |
|---|---|
| 1 | С помощью равнобедренного треугольника можно построить угол в точке, имеющий определенную меру. Для этого каждая сторона равнобедренного треугольника будет равна измеряемому углу. |
| 2 | Равнобедренный треугольник также может использоваться для нахождения угла между двумя прямыми. При этом равные стороны треугольника будут соответствовать прямым, а третья сторона – перпендикулярному отрезку, соединяющему прямые. |
2. Нахождение геометрических середин
Равнобедренные треугольники активно применяются для нахождения геометрических середин отрезков. Если равнобедренный треугольник лежит на отрезке, то его вершина будет совпадать с серединой этого отрезка, что удобно использовать при делении прямой на равные части.
3. Решение геометрических задач
Равнобедренные треугольники – это мощный инструмент для решения геометрических задач. Зная информацию о равных сторонах или углах равнобедренного треугольника, можно найти другую информацию об этом треугольнике, например, длины других сторон или другие углы.