В наше время, когда мы сталкиваемся со множеством файлов и программ, играющих важную роль в нашей повседневной жизни, величина объема информации играет огромную роль. Однако, существует определенная путаница, когда речь заходит о мегабайтах (МБ) и килобайтах (КБ). Интересно отметить, что 1 мегабайт не равен 1000 килобайтам, а равен 1024 килобайтам. А вот почему...
Вся эта путаница связана с системой счисления, которую мы используем в наших электронных устройствах. В основе этой системы лежит двоичная система счисления, в которой все числа представлены только двумя цифрами - 0 и 1. Когда мы говорим о единицах измерения информации, мы имеем дело с битами и байтами. Бит - это самая маленькая единица измерения информации, а байт состоит из 8 бит.
Как определено значение 1 мб

Двоичная система счисления использует два символа - 0 и 1, и каждый последующий разряд увеличивается в два раза. Например, в двоичной системе счисления число 2 представляется как 10, число 4 - 100, число 8 - 1000 и так далее.
Именно поэтому значение 1 мегабайта равно 1024 килобайтам, так как 1024 - это ближайшая степень двойки, которая составляет 2^10. Использование именно этого значения позволяет оптимально использовать память компьютерных устройств.
Однако, стоит отметить, что в некоторых сферах применяется значение 1 мегабайта равное 1000 килобайтам, что связано с использованием десятичной системы счисления. Например, в накопителях данных таких как флеш-драйвы или жесткие диски, производители часто устанавливают значение 1 мегабайта равным 1000 килобайтам.
Единицы измерения информации
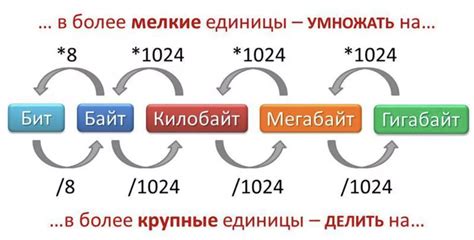
Единицы измерения информации используются для определения объема данных, который может быть передан или хранится на устройствах. Важно помнить, что единицы измерения информации основаны на двоичной системе счисления, где каждая последующая единица в два раза больше предыдущей.
Наиболее распространенными единицами измерения информации являются бит (binary digit) и байт (byte). Бит - это самая маленькая единица информации, которая может принимать два значения: 0 или 1. Байт, в свою очередь, состоит из 8 битов.
Когда речь идет о хранении данных на компьютере или передаче через сети, обычно используются крупные единицы измерения информации: килобайт (KB), мегабайт (MB), гигабайт (GB) и терабайт (TB).
Но почему в 1 мегабайте содержится 1024 килобайта, а не 1000, как в других системах измерения?
Это связано с особенностями двоичной системы счисления, которая является основой для работы компьютеров. В двоичной системе счисления каждый бит может принимать значения 0 или 1. В двоичной системе число 2 является основой, поэтому каждая следующая единица измерения увеличивается в 2 раза.
В результате, один килобайт (KB) состоит из 1024 байт, один мегабайт (MB) - из 1024 килобайт, один гигабайт (GB) - из 1024 мегабайт, и так далее.
Несмотря на то, что в основной жизни принято использовать десятичную систему счисления, в компьютерных науках используется двоичная система измерения информации. Поэтому 1 мегабайт (MB) содержит 1024 килобайта (KB), а не 1000 как в других областях.
История использования бинарного представления данных

Понятие бинарного представления данных возникло в середине XX века, когда начался активный процесс разработки и использования электронных компьютеров. Перед этим, данные записывались и обрабатывались в десятичной системе счисления, используя различные символы и конструкции.
Однако, с появлением электронных компьютеров стало очевидно, что использование десятичной системы счисления накладывает ограничения на объем и скорость обработки данных. К примеру, в десятичной системе счисления для представления числа от 0 до 9 требуется 10 различных символов, а в двоичной системе для представления числа от 0 до 1 требуется всего 2 символа.
Это позволило значительно увеличить емкость памяти компьютеров и скорость выполнения операций. Вместо того, чтобы использовать длинные последовательности символов для представления чисел и других данных, компьютеры начали использовать короткие двоичные коды, что существенно экономило ресурсы и улучшало эффективность работы.
Основой бинарного представления данных стала техника, называемая "выброс данных", которая позволяет представить любой вид информации, в том числе текст, звук и видео, в виде последовательности двоичных символов, состоящих из 0 и 1.
С течением времени, бинарное представление данных стало основой для разработки и использования различных форматов файлов (например, BMP, MP3, AVI), а также протоколов передачи данных (например, TCP/IP), что позволило создать единую систему обмена информацией между компьютерами и различными устройствами.
- Бинарное представление данных широко применяется в современных информационных технологиях, таких как компьютерная графика, аудио- и видео-кодирование, цифровая обработка сигналов и других областях.
- Бинарное представление данных позволяет достичь высокой скорости и эффективности обработки информации, а также обеспечивает надежность и безопасность хранения и передачи данных.
- Развитие бинарного представления данных постоянно продолжается, и современные технологии позволяют более эффективно кодировать и обрабатывать информацию с использованием современных алгоритмов и методов.
Биты и байты в компьютерах

Когда мы говорим о хранении данных в компьютере, часто используются такие термины, как биты и байты. Чтобы понять, почему в 1 МБ находится 1024 КБ, нам необходимо разобраться в основах информатики.
Вся информация в компьютере представлена с помощью двоичной системы счисления, в которой есть всего две цифры: 0 и 1. Каждая единица и ноль в этой системе называется битом.
Бит – это самая маленькая единица информации, которую можно хранить или передавать в компьютере. Он может принимать только два значения: 0 или 1.
Один байт состоит из 8 бит. Байт – это базовая единица измерения информации в компьютере. Большинство символов и чисел могут быть представлены одним байтом.
Если мы сделаем простой расчет, умножив количество байт в мегабайте (1024) на количество бит в байте (8), получим объем в битах. Затем, разделив его на 1024, можно получить объем в килобитах, и так далее.
Однако, когда мы говорим о мегабайтах, килобайтах и гигабайтах, мы часто используем двоичную систему, в которой каждый следующий уровень имеет значение, увеличивающееся в десять раз. Это объясняет разницу между 1 МБ (1024 КБ) и 1 ГБ (1024 МБ).
Что такое система счисления в компьютерах

Основной причиной использования двоичной системы счисления в компьютерах является особенность работы электронных компонентов, которые способны различать только два состояния – открытое и закрытое. Каждый бит в компьютере представляет собой одну такую электронную составляющую и может быть в состоянии 0 (открыто) или 1 (закрыто).
Для удобства представления больших чисел в компьютерах используется префиксное обозначение единиц измерения информации. Так, 1 килобайт (Кб) представляет собой 1024 байта, а не 1000 байт, как это принято в десятичной системе счисления. Это связано с тем, что в двоичной системе основание числа – 2, а 2 в степени 10 равно 1024.
Таким образом, использование двоичной системы счисления и префикса 1024 позволяет компьютерам более удобно работать с большими объемами информации, сохраняя при этом точность вычислений.
Основание двоичной системы
Основанием системы счисления является число, которое определяет количество различных цифр, которыми можно представить числа. В десятичной системе счисления, которую мы обычно используем в повседневной жизни, основание равно 10, поскольку имеется 10 различных цифр от 0 до 9.
Однако в двоичной системе счисления основание равно 2, поскольку нас интересуют только две различные цифры - 0 и 1. Таким образом, каждая позиция числа в двоичной системе обозначает степень числа 2, начиная с нуля. Например, число 101 в двоичной системе означает 1 * 2^2 + 0 * 2^1 + 1 * 2^0, что равно 4 + 0 + 1, или 5 в десятичной системе счисления.
Почему же в 1 МБ 1024 КБ? Проблема в том, что данные в компьютерах обрабатываются в двоичной системе счисления, и из-за специфики математики двоичной системы удобнее использовать числа, которые являются степенями числа 2. 1024, или 2^10, является удобным числом, которое близко к 1000 и позволяет легко представлять большие объемы данных в компьютерах.
Таким образом, в компьютерной науке принят стандарт, согласно которому 1 МБ равно 1024 КБ, а не 1000 КБ, как в десятичной системе счисления. Это объясняется основанием двоичной системы счисления и позволяет удобно работать с объемами данных в компьютерных системах.
Связь между двоичной и десятичной системами счисления

Перевод чисел между двоичной и десятичной системами счисления осуществляется по принципу, что каждый разряд числа в двоичной системе умножается на соответствующую степень числа 2 и складывается. Для примера, двоичное число 1010 можно перевести в десятичное, используя приведенную выше формулу.
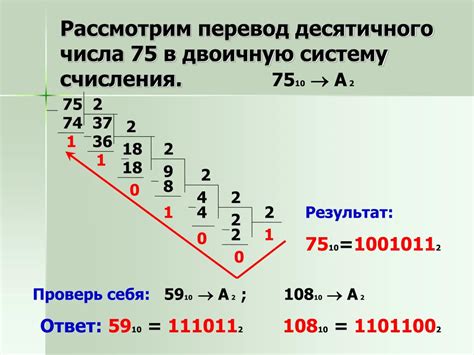
Также, десятичные числа можно перевести в двоичные, используя метод деления на 2. При этом, остатки от деления на 2 записываются в обратном порядке, чтобы получить двоичное представление числа. Например, число 10 можно перевести в двоичное, следуя следующему алгоритму:
- Деление числа 10 на 2 дает остаток 0 и частное 5
- Деление числа 5 на 2 дает остаток 1 и частное 2
- Деление числа 2 на 2 дает остаток 0 и частное 1
- Деление числа 1 на 2 дает остаток 1 и частное 0
Значения остатков записываются в обратном порядке, таким образом, получается двоичное представление числа 10 - 1010.
Связь между двоичной и десятичной системами счисления имеет важное значение в компьютерной науке. Компьютеры используют двоичную систему счисления для представления и обработки данных, поэтому понимание этой связи необходимо для разработки и анализа программного обеспечения.
Понятие перевода бинарного значения в десятичное значение

Однако в повседневной жизни, мы привыкли мыслить в десятичной системе счисления, где используются десять цифр, от 0 до 9. Иногда возникает необходимость перевести число из двоичной системы в десятичную систему для более привычного понимания.
Для выполнения такого преобразования можно использовать следующий алгоритм:
- Начните с правой стороны бинарного числа и присвойте первой цифре значение 1.
- Умножьте это значение на 2 и двигайтесь слева направо, присваивая каждой следующей цифре удвоенное значение предыдущей цифры.
- Продолжайте этот процесс до тех пор, пока не достигнете крайней левой цифры.
- Сложите все полученные значения, чтобы получить десятичное представление исходного числа.
Например, пусть дано двоичное число 1011. Следуя алгоритму, мы получим:
1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 8 + 0 + 2 + 1 = 11
Таким образом, двоичное число 1011 в десятичной системе равно 11.
С помощью этого алгоритма можно преобразовать любое двоичное число в десятичное, чтобы лучше понять его значение в контексте десятичной системы счисления, с которой мы обычно сталкиваемся в повседневной жизни.