Формула Шеннона, названная в честь американского ученого Клода Шеннона, является одной из основных формул в информационной теории. Она используется для определения количества информации, содержащегося в сообщении, и для оценки производительности коммуникационных систем. Однако, в некоторых случаях, формула Шеннона может давать отрицательное значение, что вызывает недоумение и вопросы.
Причиной отрицательного значения формулы Шеннона является наличие последствий ошибки при декодировании информации. Формула Шеннона рассматривает информацию как случайную величину, которая измеряется в битах. Когда сообщение декодируется без ошибок, значение формулы будет положительным, но если происходит ошибка в декодировании, значение может стать отрицательным.
Отрицательное значение формулы Шеннона означает, что вероятность ошибки в декодировании превышает вероятность правильного декодирования. Это может быть связано с различными факторами, такими как шум, искажения, или несовершенство коммуникационной системы. В таких случаях, формула Шеннона показывает, что передача информации является неэффективной и требует улучшения системы коммуникации.
Понятие формулы Шеннона
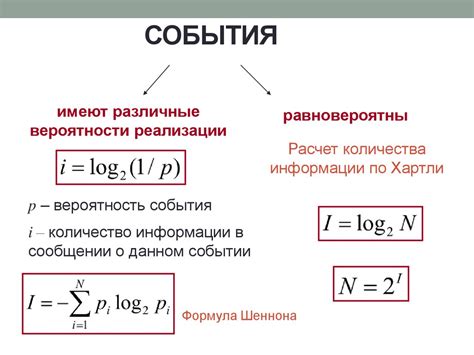
Основная идея формулы Шеннона заключается в преобразовании сообщения в последовательность символов, которые представляют собой информацию. Шеннон определил количество информации как количество бит, необходимых для передачи сообщения.
В формуле Шеннона используется логарифм, чтобы определить количество возможных комбинаций символов, которые могут быть использованы для представления сообщения. Чем больше количество возможных комбинаций, тем больше информации содержится в сообщении.
Формула Шеннона выглядит следующим образом:
H = -∑(p(x) * log2(p(x)))
Где H - количество информации в сообщении, p(x) - вероятность появления символа x в сообщении.
Формула Шеннона имеет отрицательное значение, так как логарифм от вероятности символа x меньше 1. Значение формулы Шеннона позволяет определить минимальное количество бит, которое необходимо для кодирования сообщения.
Основные компоненты формулы Шеннона

| Символ | Описание |
|---|---|
| H | Энтропия или средняя степень неопределенности сообщения. Она измеряется в битах и показывает, насколько случайным или неожиданным является сообщение. |
| P(x) | Вероятность появления определенного символа (x) в сообщении. Это вероятность выбора данного символа из всего множества символов. |
| log | Логарифм по основанию 2. Он используется для измерения количества бит, необходимых для кодирования сообщения. |
Используя эти компоненты, формула Шеннона вычисляет количественное значение информации, исходя из степени неопределенности сообщения и вероятности появления определенных символов.
Согласно формуле Шеннона, информация может быть представлена в виде последовательности битов, где каждый бит представляет собой выбор между двумя альтернативными состояниями. Таким образом, формула Шеннона помогает нам понять, насколько эффективно мы можем передавать информацию и какой объем памяти она занимает.
Применение формулы Шеннона в информационной теории
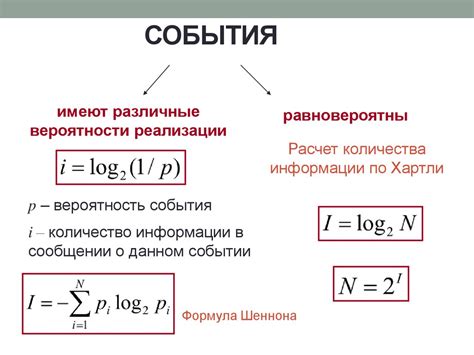
Применение формулы Шеннона широко распространено в различных областях, связанных с информацией и коммуникациями, таких как телекоммуникации, компьютерные сети, компрессия данных и даже в криптографии.
Формула Шеннона позволяет вычислить количество информации, выраженное в битах, необходимое для передачи определенного сообщения или набора данных. Она основывается на понятии энтропии, которая измеряет степень неопределенности или неожиданности информации.
Применение формулы Шеннона позволяет эффективно сжимать данные, то есть уменьшать количество битов, необходимых для их хранения и передачи. Это важно, например, для уменьшения объема передаваемой информации по сетям с ограниченной пропускной способностью или для сохранения места на устройствах хранения данных.
Кроме того, формула Шеннона помогает оптимизировать процесс кодирования и декодирования информации, что позволяет увеличить скорость и эффективность передачи данных. Она также находит применение в области криптографии, где используется для оценки стойкости криптографических алгоритмов и систем защиты информации.
- Использование формулы Шеннона позволяет достичь оптимального уровня сжатия данных при минимальных потерях информации.
- Эта формула также имеет применение при проектировании и разработке коммуникационных систем и сетей для определения требуемой пропускной способности и оценки качества передачи данных.
- Формула Шеннона является ключевым инструментом для анализа и оптимизации эффективности передачи информации, и она широко используется специалистами во многих областях, связанных с обработкой и передачей данных.
Таким образом, применение формулы Шеннона в информационной теории позволяет оценить количество информации, сжать данные и оптимизировать передачу информации, играя важную роль в различных областях, связанных с обработкой и передачей данных.
Откуда берется отрицательное значение формулы Шеннона

Отрицательное значение формулы Шеннона возникает в случаях, когда вероятность появления определенного символа или бита близка к нулю. При этом единичное значение логарифма log2(pi) в данном случае становится положительным. Умножение на отрицательную вероятность pi приводит к получению отрицательного значения суммы внутри суммы Σ(pi) * log2(pi).
Отрицательное значение формулы Шеннона указывает на то, что сообщение содержит информацию, которая является редкой или неожиданной. Такие низкопробабильные события или символы обладают большей информационной ценностью, так как они предоставляют больше новой информации по сравнению с более вероятными событиями или символами.
Отрицательное значение формулы Шеннона не является ошибкой или несостоятельностью формулы. Оно просто отражает особенности конкретного сообщения или источника информации.
Последствия отрицательного значения формулы Шеннона

Отрицательное значение формулы Шеннона указывает на необычность или ошибку в сообщении. Это может быть вызвано неправильным кодированием, потерей данных или проблемами с передачей информации. Наличие отрицательного значения может означать, что сообщение содержит более высокую степень неопределенности, чем ожидалось.
Последствия отрицательного значения формулы Шеннона могут быть различными. Во-первых, это может привести к трудностям в декодировании сообщения и понимании его содержания. Также, отрицательное значение может указывать на наличие ошибок или искажений в данных, что может привести к неправильным решениям или неверной интерпретации информации. Кроме того, отрицательное значение может быть признаком наличия шума или помех в процессе передачи информации.
В целом, отрицательное значение формулы Шеннона является сигналом о проблемах или необычностях в сообщении. Это требует дополнительного анализа и внимания для устранения ошибок, улучшения качества передачи информации и достижения более точных результатов.
| Последствия отрицательного значения формулы Шеннона: |
|---|
| - Трудности в декодировании сообщения |
| - Возможное наличие ошибок или искажений в данных |
| - Неправильные решения или неверная интерпретация информации |
| - Признак наличия шума или помех в процессе передачи информации |
Критика формулы Шеннона с отрицательным значением
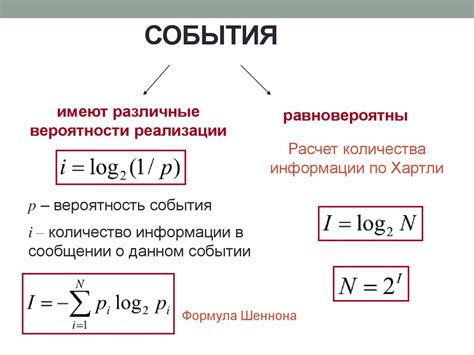
Отрицательное значение информации, полученное по формуле Шеннона, вызывает сомнения в ее применимости и точности. Некоторые исследователи считают, что это свидетельствует о неполноте и недостаточности данной формулы для определения информации.
Одной из критик формулы Шеннона с отрицательным значением является невозможность условной информации быть меньше нуля. Согласно формуле Шеннона, условная информация вычисляется как разность между общей информацией и информацией о предыдущих символах. Если информационная единица, например, символ или бит, встречается чаще, чем ожидается, то условная информация может быть отрицательной.
Также критикам не нравится тот факт, что формула Шеннона не учитывает контекст и особенности передачи информации. Она не учитывает возможности улучшения канала связи, устранения шума или использования кодирования для более эффективной передачи информации.
Однако, несмотря на критику и ограничения, формула Шеннона все еще широко используется в различных областях, таких как компьютерная наука, связь и информационные технологии. Она является основой для разработки различных алгоритмов и протоколов связи, и в целом привносит важное понятие информации и ее передачи.
Возможные исправления формулы Шеннона

Возможные исправления формулы Шеннона могут включать в себя:
- Введение дополнительных ограничений на входные данные. Например, можно предусмотреть, что входные данные не могут содержать отрицательные значения или значения, превышающие определенный порог.
- Использование модифицированной формулы, которая учитывает особенности конкретной задачи. Например, для кодирования адаптивного видеопотока можно использовать формулу, которая учитывает статистику изменений в видеопоследовательности и адаптирует передаваемую информацию в зависимости от текущего состояния.
- Разработка более сложных алгоритмов компрессии данных, которые позволяют получить более точные и надежные результаты без отрицательных значений. Например, можно использовать методы адаптивной компрессии, которые основываются на изменении размера блока компрессии в зависимости от содержимого данных.
Важно отметить, что исправления формулы Шеннона должны основываться на тщательном анализе конкретной проблемы и учете ее особенностей. Кроме того, необходимо учитывать, что любые модификации могут повлечь за собой дополнительные затраты вычислительных ресурсов и увеличение сложности алгоритмов.
В итоге, возможные исправления формулы Шеннона должны быть тщательно обдуманы и протестированы, чтобы обеспечить правильные и надежные результаты без отрицательных значений.



