Логарифмы являются важным понятием в математике и широко используются в различных областях, включая физику, экономику, компьютерные науки и другие. Ключевой характеристикой логарифма является его основание, которое определяет, по какому числу производится логарифмирование.
Основание логарифма определяет, как число возводится в степень, чтобы получить заданное число. Например, для натурального логарифма (основание e) число e возводится в степень, чтобы получить исходное число. Таким образом, ln(e) = 1.
Однако, почему основание логарифма не равно 1? Если бы основание логарифма было равно 1, то логарифмирование было бы бесполезным. Все числа, включая 0 и 1, имели бы логарифм равный 0. Это вызвано тем, что 1 возводится в любую степень, всегда равную 1. Таким образом, логарифм с основанием 1 не имеет смысла и не предоставляет никакой полезной информации.
Поэтому, основание логарифма обычно выбирается отличным от 1, чтобы обеспечить его полезность и удобство. Например, наиболее распространенными основаниями являются 10 (обычный логарифм) и e (натуральный логарифм). Они широко используются в различных областях науки и техники для решения сложных задач и моделирования различных процессов.
Почему основание логарифма не равно 1?

Если основание логарифма было равно 1, то все логарифмы становились бы равными друг другу и не имели бы отличительных свойств. Например, для всех x: log1(x) = 0, потому что 1 в любой степени равно 1. Это означало бы, что логарифмы с разными основаниями не отличались бы друг от друга.
Выбор основания логарифма зависит от конкретной задачи или контекста. В наиболее распространенной системе - системе десятичных логарифмов - основание равно 10. В компьютерных науках часто используется система двоичных логарифмов с основанием 2.
Логарифмы с разными основаниями имеют различные свойства и применяются в различных областях математики, науки и инженерии. Преимущества выбора определенного основания логарифма зависят от контекста, задачи и предпочтений исследователя.
Ключевая информация о логарифмах:

Основание логарифма обычно выбирается таким образом, чтобы облегчить расчеты или удовлетворить требованиям конкретной задачи. В наиболее распространенной системе, называемой натуральным логарифмом, основание равно числу e, которое является математической константой, приближенно равной 2,71828.
При выборе основания логарифма нужно учитывать, что различные основания логарифма соответствуют различным шкалам измерения. Например, при использовании основания 10 логарифма получаются десятичные логарифмы, которые широко используются в науке и инженерии. Основание 2 дает двоичные логарифмы, которые встречаются в информатике и теории информации.
Важно отметить, что логарифм с основанием 1 не существует, так как любое число, возведенное в степень 0, равно 1. Поэтому основание логарифма должно быть больше 1, чтобы логарифм был определенным и имел смысл.
Понятие логарифма

Логарифмы имеют много применений и встречаются в различных областях науки, инженерии и финансов. Они используются для решения уравнений, упрощения сложных выражений, измерения амплитуды звуков и света, моделирования роста и распространения, анализа данных и т.д.
Обозначают логарифмы символом "log". Если основание логарифма не указано, то подразумевается, что основание равно 10. В этом случае логарифм числа х обозначается как log10 (x), или просто log(x).
Однако основание логарифма может быть любым положительным числом, кроме 1. Если основание равно 1, то логарифм не имеет смысла, так как все степени числа 1 равны 1, и нет способа найти показатель степени.
Основаниями логарифма, которые наиболее часто используются, являются основание 10 (для десятичных логарифмов) и основание e (для натуральных логарифмов).
Различные основания логарифмов
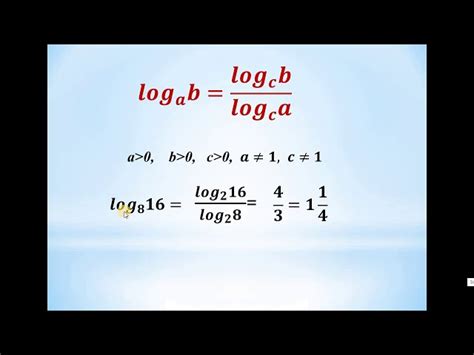
Основание логарифма определяет, к какому числу нужно возвести основание, чтобы получить подлогарифмическое число. Например, если основание равно 10, то логарифм числа 10000 по основанию 10 будет равен 4, так как 10 в четвертой степени равно 10000. А если основание равно 2, то логарифм числа 16 будет равен 4, так как 2 в четвертой степени также равно 16.
Наиболее часто используется естественный логарифм с основанием экспоненты e, который примерно равен 2,71828. Естественный логарифм обладает множеством интересных свойств и широко применяется в различных областях науки и инженерии.
Другими распространенными основаниями логарифмов являются 2 и 10. Логарифмы по основанию 2 удобны при работе с двоичными числами и компьютерными алгоритмами, а логарифмы по основанию 10 используются при работе с десятичными значениями, такими как денежные суммы или измерения величин.
Также существуют логарифмы с другими основаниями, например, логарифмы по основанию 3, 5, или любому другому положительному числу.
Использование различных оснований логарифмов зависит от конкретной задачи и предпочтений того, кто выполняет вычисления. Важно помнить, что результат вычисления логарифма будет зависеть от выбранного основания.
| Основание | Пример |
|---|---|
| 10 | log10 100 = 2 |
| 2 | log2 16 = 4 |
| e | ln(e) = 1 |
Примеры использования логарифмов

Логарифмы находят применение в различных областях науки и техники. Они позволяют упростить вычисления и решить задачи, которые связаны с экспоненциальным ростом или убыванием величин.
Одним из примеров использования логарифмов является измерение уровня звука. Звучание звука определяется амплитудой колебаний воздуха, и эта величина может быть очень большой. Чтобы удобно работать с такими значениями, используют децибелы – логарифмическую шкалу. Так, каждое увеличение уровня звука на 10 децибел соответствует удвоению амплитуды колебаний.
В математике логарифмы также используются для решения уравнений и нахождения аналитических решений задач. Например, логарифмы широко применяются в физике для описания различных процессов, таких как затухание волн, распространение тепла и другие.
Еще одним примером использования логарифмов является статистика. Логарифмы позволяют сгладить экстремальные значения и представить данные в более удобной форме. Например, логарифмическая шкала может быть использована для представления доходности финансовых инструментов или роста популяции.
Кроме того, логарифмы широко применяются в информатике, особенно в алгоритмах сжатия данных. Они позволяют эффективно сжимать информацию, сохраняя при этом ее важные свойства.
Это лишь некоторые примеры применения логарифмов. Все они демонстрируют важность и универсальность этой математической функции.



