Векторное произведение – одно из фундаментальных понятий линейной алгебры, которое находит широкое применение в различных областях науки и техники. Векторное произведение определяется для двух векторов в трехмерном пространстве и представляет собой вектор, перпендикулярный плоскости, образованной этими двумя векторами.
Одним из важных свойств векторного произведения является его геометрическое значение – площадь параллелограмма, образованного двумя векторами. Площадь параллелограмма можно найти, используя модуль векторного произведения и синус угла между векторами. Таким образом, векторное произведение позволяет не только находить вектор, перпендикулярный данным векторам, но и определять площадь образованного ими параллелограмма.
Интересно отметить, что векторное произведение обладает свойством антикоммутативности – изменение порядка векторов в произведении приводит к изменению его знака. Это свойство позволяет использовать векторное произведение для определения ориентации параллелограмма – векторное произведение будет направлено перпендикулярно к плоскости, образованной векторами, тем самым намекая на основные свойства геометрического объекта.
Что такое векторное произведение?

Математически векторное произведение двух векторов a и b определяется как:
| a x b = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1) |
где a1, a2, a3 и b1, b2, b3 - компоненты векторов a и b соответственно.
Векторное произведение имеет несколько важных геометрических значений.
Во-первых, результат векторного произведения является вектором, перпендикулярным исходным векторам a и b. Это означает, что векторное произведение может использоваться для определения нормали к плоскости, образованной этими векторами.
Во-вторых, модуль векторного произведения равен площади параллелограмма, построенного на исходных векторах a и b. Это свойство векторного произведения позволяет вычислять площади фигур в трехмерном пространстве.
Векторное произведение широко используется в физике, геометрии и инженерии для решения задач, связанных с векторами и трехмерной геометрией. Оно позволяет анализировать форму и ориентацию объектов в пространстве и находить их взаимное расположение.
Формула для расчета площади параллелограмма
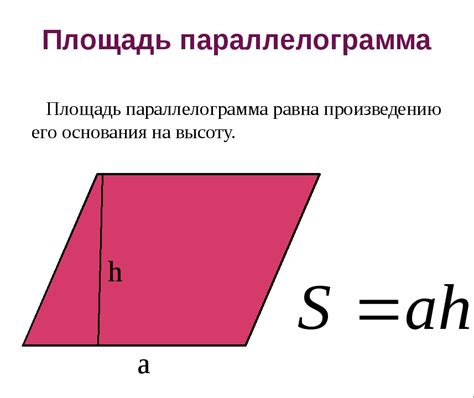
Площадь параллелограмма можно вычислить с помощью векторного произведения его сторон. Для этого применяется следующая формула:
S = |a x b|,
где a и b - векторы, соответствующие сторонам параллелограмма, а символ |a x b| обозначает модуль векторного произведения. Модуль векторного произведения равен площади параллелограмма.
Связь векторного произведения с геометрическим значением
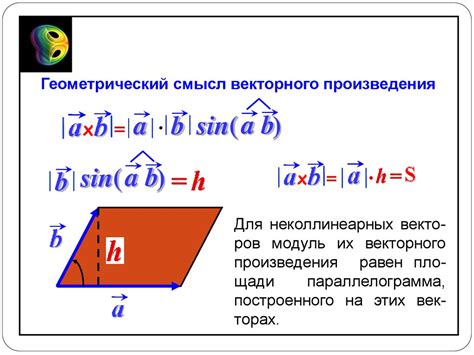
Векторное произведение двух векторов A и B можно выразить следующей формулой:
A × B = |A| |B| sin(θ) n
Здесь |A| и |B| обозначают длину векторов A и B соответственно, θ - угол между ними, а n - единичный вектор, перпендикулярный плоскости образованной векторами A и B.
Геометрическое значение векторного произведения заключается в том, что его длина равна площади параллелограмма, образованного векторами A и B. Таким образом, площадь параллелограмма можно вычислить с помощью формулы:
Площадь = |A × B| = |A| |B| sin(θ)
Это может быть полезно в решении задач, связанных с расчетом площадей поверхностей, объемов тел и других геометрических задач.
Векторное произведение также имеет другие геометрические значения. Например, оно позволяет определить направление и нормаль к плоскости, образованной векторами, а также может быть использовано для нахождения проекции вектора на плоскость.
Таким образом, векторное произведение имеет глубокую связь с геометрическим значением и является мощным инструментом для решения геометрических задач и изучения свойств векторов и плоскостей.
Геометрическое интерпретирование векторного произведения

Векторное произведение двух векторов имеет геометрическую интерпретацию, которая позволяет нам лучше понять его смысл и значение. Когда мы берем два вектора и вычисляем их векторное произведение, мы получаем результат, который имеет не только значения величины и направления, но и геометрическое значение.
Геометрический смысл векторного произведения заключается в том, что результатом операции является вектор, перпендикулярный плоскости, образованной исходными векторами. Он имеет длину, равную площади параллелограмма, построенного на этих векторах.
Другими словами, векторное произведение двух векторов представляет собой новый вектор, который также является нормалью к плоскости, образованной этими векторами. Это означает, что новый вектор перпендикулярен к плоскости, и его направление определено согласно "правилу буравчика".
Важно отметить, что направление векторного произведения имеет свою особенность - оно зависит от порядка следования исходных векторов. Если поменять их местами, то направление вектора также изменится, но его длина останется неизменной.
Таким образом, геометрическое значение векторного произведения позволяет нам более наглядно представить его смысл. Оно указывает на важные свойства исходных векторов и позволяет решать различные геометрические задачи.
Примеры применения векторного произведения в геометрии

1. Нахождение площади параллелограмма:
Для нахождения площади параллелограмма, образованного двумя векторами a и b, можно использовать векторное произведение. Площадь параллелограмма можно выразить следующей формулой:
Площадь = ∥(a × b)∥
где ∥(a × b)∥ - длина вектора, полученного векторным произведением a и b. Таким образом, векторное произведение позволяет легко и точно вычислить площадь параллелограмма.
2. Определение перпендикулярности:
Векторное произведение также используется для определения перпендикулярности двух векторов. Если векторное произведение двух векторов равно нулю, то это означает, что векторы перпендикулярны друг другу. Это полезное свойство векторного произведения позволяет определить, являются ли два вектора взаимно перпендикулярными или нет.
3. Нахождение нормали к плоскости:
Векторное произведение также используется для нахождения нормали к плоскости, заданной двумя векторами. Нормаль к плоскости - это вектор, перпендикулярный плоскости. Для нахождения нормали к плоскости можно использовать векторное произведение этих двух векторов. Результатом будет вектор, направленный перпендикулярно к плоскости.
Это лишь некоторые примеры применения векторного произведения в геометрии. Векторное произведение широко используется для решения задач, связанных с реальным миром и анализом геометрических структур.