Бесконечность - одно из самых загадочных явлений в математике. Исследование бесконечностей возникло в процессе попыток ученых понять, как применять математические операции к неопределенностям. Однако степень бесконечности оказалась особенно противоречивой и вызывающей неопределенность. Чтобы понять, почему это происходит, необходимо рассмотреть основные аспекты бесконечности.
Бесконечность может быть представлена различными способами: бесконечное возрастание числовой последовательности, бесконечное увеличение площади геометрической фигуры и т. д. Однако степень бесконечности - это совсем другая история. Когда мы говорим о степени бесконечности, мы обозначаем количество возможных комбинаций или вариантов.
Неопределенность возникает, потому что это количество может быть бесконечным в разных контекстах. Например, в математике мы можем говорить о количестве натуральных чисел, рациональных чисел или действительных чисел. Каждая из этих степеней бесконечности имеет свои особенности и вызывает свою неопределенность.
Почему бесконечности в степени вызывают неопределенность?

Сначала давайте определим, что такое бесконечность. В математике бесконечность - это понятие, обозначающее отсутствие конечной границы или ограничения. Она может быть представлена положительной бесконечностью (+∞), отрицательной бесконечностью (-∞) или просто как бесконечность (∞).
Когда мы говорим о бесконечности в степени, мы подразумеваем возведение числа или переменной в бесконечную степень. Например, 2 возводится в бесконечную степень, записывается как 2^∞.
Однако, проблема с бесконечностями в степени заключается в том, что они могут привести к различным результатам в разных математических контекстах.
Из-за отсутствия конечной границы, бесконечность в степени может привести к неоднозначным и неопределенным результатам. Например, если мы возведем число 2 в бесконечную степень, мы можем получить результат как 0, так и ∞ в зависимости от способа подхода к задаче.
Это вызывает неопределенность, поскольку мы не можем однозначно сказать, какой результат является правильным. Одна математическая система может допустить одно значение, в то время как другая - другое.
Это также связано с проблемой бесконечностей, которые могут быть более "великими" или "меньшими". Например, существует разница между бесконечностью (∞) и бесконечностью плюс бесконечность (+∞∞).
В зависимости от контекста и правил, заданных в математической системе, бесконечности в степени могут быть интерпретированы по-разному, что в конечном итоге вызывает неопределенность и путаницу.
Таким образом, бесконечности в степени вызывают неопределенность из-за отсутствия конечной границы и разных интерпретаций, зависящих от контекста и правил математической системы.
Математическое определение бесконечности
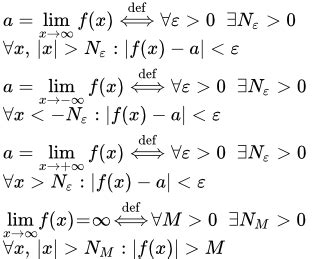
Абстрактное понятие бесконечности обычно обозначается символом ∞ или используется специальными формулировками для представления границы или предела, который не достижим или неопределенный.
В математике существует несколько видов бесконечности, которые различаются своими свойствами и используются в различных областях:
- Бесконечность как число – бесконечные числа, отсутствие конечного значения, такие как бесконечные десятичные дроби или бесконечные периодические десятичные дроби.
- Бесконечность как предел – концепция бесконечно больших и бесконечно малых величин, которые приближаются к бесконечности или близки к нулю.
- Бесконечность как мощность – понятие, связанное с количеством элементов в бесконечном множестве, таких как бесконечные последовательности или бесконечные множества чисел.
Бесконечность в математике является важным и сложным концептом, который часто используется для описания и анализа различных математических структур и процессов. Она позволяет расширить и уточнить понятия и методы математики, а также дает возможность решать задачи, которые не могут быть описаны конечными значениями или пределами.
Ограниченность и неограниченность
В математике понятие ограниченности и неограниченности играет важную роль при рассмотрении степеней бесконечности. Ограниченность означает, что объект или функция имеют верхнюю и нижнюю границы, в то время как неограниченность подразумевает отсутствие границ.
Когда мы говорим о степенях бесконечности, возникает неопределенность потому, что понятие неограниченности в данном контексте представляет собой особую форму ограниченности. На первый взгляд может показаться парадоксальным, что степенная функция, устремляющаяся к бесконечности, может быть одновременно ограниченной. Однако, это объясняется тем, что в данном случае неограниченность означает отсутствие конечной верхней или нижней границы, но не отсутствие границ вовсе.
Для лучшего понимания этого парадокса, рассмотрим пример с функцией f(x) = 1/x. При x, стремящемся к бесконечности, значение функции будет стремиться к нулю. Хотя значения функции не будут иметь конкретной верхней границы, они все равно ограничены возможностью достичь нуля.
Эта неопределенность связана с особенностями работы с бесконечно большими и бесконечно малыми значениями. В таких случаях, для полного определения степени бесконечности, дополнительные условия или более точные определения могут потребоваться.
Операции с бесконечностями

В математике существует понятие бесконечности, которое вызывает неопределенность во многих операциях. Бесконечность может быть положительной (∞), отрицательной (-∞) или бесконечностью отсутствия (∞-∞).
Одной из основных операций с бесконечностями является сложение. Для положительной бесконечности (∞), сложение с любым другим числом, кроме отрицательной бесконечности (-∞), даёт бесконечность. Например, ∞ + 5 = ∞. Если же сложить положительную бесконечность с отрицательной бесконечностью, результатом будет неопределенность (∞ - ∞).
Вычитание с бесконечностями также вызывает неопределенность. Если от положительной бесконечности (∞) вычесть положительную бесконечность (∞), результатом будет неопределенность (∞ - ∞). Также неопределенность будет, если вычесть отрицательную бесконечность (-∞) из любой другой бесконечности (∞ - (-∞)).
Умножение с бесконечностями также имеет свои особенности. Умножение положительной бесконечности (∞) на любое положительное число дает положительную бесконечность (∞ * n = ∞). Умножение отрицательной бесконечности (-∞) на любое положительное число дает отрицательную бесконечность (-∞ * n = -∞). Однако умножение нуля на бесконечность даёт неопределенность (0 * ∞).
Также следует учитывать, что деление на бесконечность тоже может вызывать неопределенность. Если число делится на положительную бесконечность, результат будет равен нулю (n / ∞ = 0). Если число делится на отрицательную бесконечность, результат будет равен нулю с отрицательным знаком (n / -∞ = -0). Однако деление бесконечности на бесконечность может дать неопределенность (∞ / ∞).
| Операция | Результат |
|---|---|
| ∞ + n | ∞ |
| ∞ + (-∞) | неопределенность (∞ - ∞) |
| ∞ - n | ∞ |
| ∞ - (-∞) | неопределенность (∞ - (-∞)) |
| ∞ * n | ∞ |
| -∞ * n | -∞ |
| 0 * ∞ | неопределенность (0 * ∞) |
| n / ∞ | 0 |
| n / -∞ | -0 |
| ∞ / ∞ | неопределенность (∞ / ∞) |



